23: Band Theory

MO Theory for Solids: Band Theory

Band Theory

MO theory for metals is slightly different but there are similar patterns that emerge.

• An MO diagram for metallic lithium.

  • Fill in the electrons for the MO pictures below.

  • Identify the HOMO and LUMO for Li₂ and Li₁₆.

    

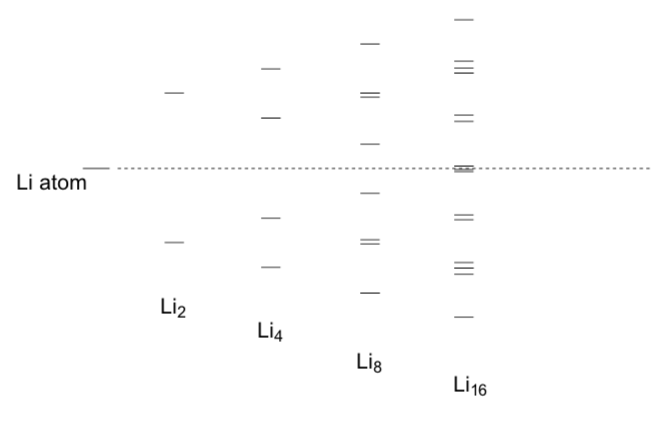
  Compare the lowest energy MO for Li2 to the lowest energy MO for Li4.

  • Which will have the longer wavelength?

  Compare the highest energy MO for Li2 to the highest energy MO for Li16.

  • Which will have the longer wavelength?

  Look for the patterns:

  1. As more Li are aggregated in the metal, lower energy orbitals, increase/decrease (circle one) in energy.

  2. As more Li are aggregated in the metal,higher energy orbitals, increase/decrease (circle one) in energy.

  3. As the number of atoms increases,energy gap between the HOMO and LUMO of Lix Increases/decreases (circle one).

  When a large number of atoms are brought together to form a solid, the number of orbitals becomes large. The energy differences between levels becomes small. Thus, in solids the levels form continuous bands of orbitals rather than discrete (separate) energy levels.

  Even a tiny sample of Li metal will have “lots” of Li atoms, Li∞. Assume you have a 1 mole of Li.

  • How many atoms is this? How many MO’s in the diagram?

  When the energy separation between adjacent MO’s is very small, we say that they have formed a band.

  Below is a sketch of the band formed by the valence orbitals in Li.

  • It is called the “s-band”. Why?

  • The shading indicates the percent occupancy (the % of orbitals that have electrons in them) of this band. Estimate the % of orbitals that are full.

  • The amount of energy needed to excite an electron from the filled band to the empty band is small/large (circle one).

    

  In band theory, the MO’s form an “electron highway” through a solid. To be highly conducting (like a metal), two things must be true:

  1. the energy separation between adjacent MO’s must be small.

  2. the orbitals must be between about 10 and 90% occupied by electrons.

  If the occupancy is less than about 10%, there aren’t enough electrons to conduct much. If it’s more than 90%, they start interfering with each other’s movement.

  • Does your band structure occupancy predict that Li is a metal?

  We can use the identical method to make an s-band structure diagram for Be.

  • Shade in the s-band to indicate the predicted electron occupancy.

    

  • Does this predict that Be would have metallic conduction?

  In reality, Be has empty p valence orbitals so a better picture of the occupancy of valence orbitals is a band formed by both s and p orbitals.

  • For Be, shade in the % occupancy for this s-p band.

    

  • Now, does this predict that Be would have metallic conduction?

  All main group metals are viewed as having overlapping s-p bands.

  • Revise your band for Li, shade in the % occupancy for this s-p band.

    

  When we did the homonuclear diatomics we were able to calculate the bond order in the molecule from the MO diagram.

  • Which type of orbitals (bonding or antibonding) are the electrons occupying in Li?

  • At what % occupancy is the cut-off between bonding and antibonding?

  • Based on your percent occupancies, which metal should have the higher “bond order”, Li or Be?

  Similarly, all transition metals are viewed as having s-d bands.

  • What is the maximum number of electrons in an s-d band?

  • For Cr, shade in the % occupancy for this s-d band.

    

Application of Band Theory: Melting Points

Melting point indicates the strength of interactions between atoms (metals) or IMF in molecular compounds.

• Fill in the s-d bands for the following metals.

• Explain the general melting point trend using band theory and the ‘sea of electrons’ theory.

Melting points (oC)

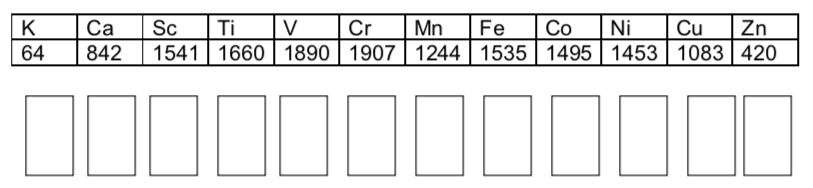
Follow up questions:

1. Suggest a reason why mercury is a liquid.

2. The alkali metals also have low melting points. Does this make sense using band theory?

3. One might predict that zinc should not be a metallic element.

   • Explain why this might be a reasonable prediction using the s-d band.

   • In fact, zinc is conducting and metallic. Consider the %occupancy for Zn if you look at the s-p-d band. Why can zinc be conducting?

Band Gap Properties of Semiconductors

Adapted from: Lisensky, Penn, Geselbracht and Ellis, J. Chem. Ed., 1992, 69 (2), 151-155.

Looking at the MO diagram for C₁₀H₂₂.

• Fill in the electrons.

  

In band theory, the orbitals containing the valence electrons is known as the valence band.

• What is this called in Frontier MO Theory (used for all the earlier MO)?

The band of unoccupied orbitals is known as the conduction band.

• What is this called in Frontier MO theory?

  

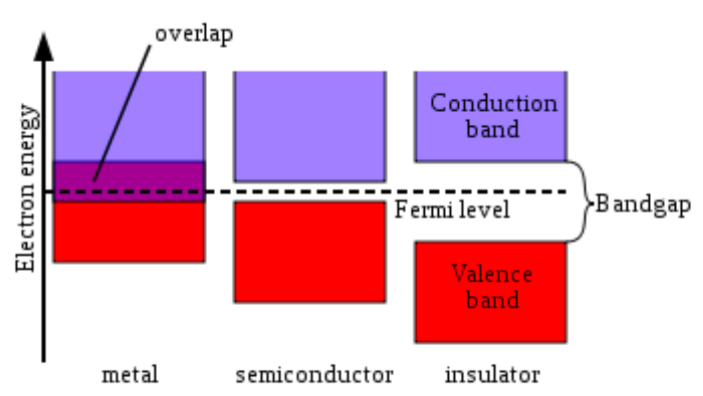
  Figure 1: Simplified diagram of the electronic band structure of metals, semiconductors, and insulators.

• Rank conductors, semiconductors and insulators in order of increasing band gap:

Based on your understanding of band theory:

• Would you predict sodium to be a:

  Conductor Semiconductor Insulator

• Would you predict C₁₀H₂₂ to be a:

  Conductor Semiconductor Insulator

Emission Spectrum

A wide range of energies can cause electrons to be excited from the valence band to the conduction band.

Excited electrons will drop from the bottom of the conduction band into the top of the valence band with an emission of light.

A light-emitting diode (LED) is a semiconductor light source. They are used in applications such as automotive lighting and traffic signals and to “read” CDs and DVDs. Infrared LEDs are also used in remote controls.

The color of the light (corresponding to the energy of the photon) is determined by the energy gap of the semiconductor.

• As the band gap energy increases, the wavelength in the emission spectrum:

  Increases or decreases

• Longer wavelengths correspond to visible

  Red or Blue

A DVD is read when a laser is passed over a track that contains small “bumps” that are squares a few hundred nm wide. To reduce errors, there must be space between bumps yet better resolution can be achieved if more information is recorded in a bump.

• Explain why a ‘blu ray’ disc might represent an advantage over a normal DVD, which is read by a laser operating at 640 nm.

Materials Used as Semiconductors

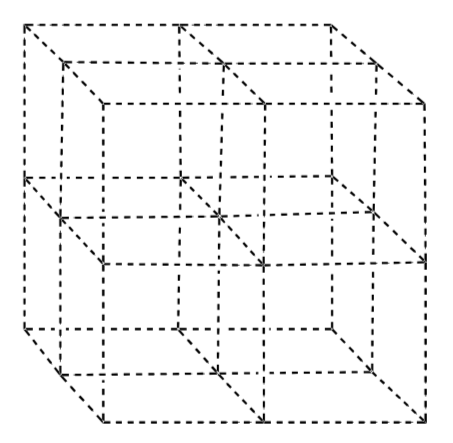
Semiconductors are typically prepared from combinations of elements having crystal structures related to that of diamond.

• Draw the diamond lattice structure.

• What is the geometry of each carbon in the diamond lattice?

• Looking at the periodic table, what other elements might be predicted to display a diamond lattice structure?

• Why?

Unit Cell of Diamond is face centered cubic structure with 1⁄2 of the tetrahedral holes filled.

• Add carbon atoms to the lattice to make the diamond unit cell.

  

• Trace a “chair” onto this structure.

Properties of Solids with Diamond Crystal Structure

Material	Unit Cell Edge Length (Å)	Bond Dissociation Energy (KJ/mol)	Band Gap Energy (eV)	Emission Wavelength (nm)
C	3.57	346	5.5	230
Si	5.43	222	1.1	1100
Ge	5.66	188	.66	1900
Sn	6.49	146	.1	12000

eV is a unit of energy

Å is 0.1 nm

In the table above,

• Which structure has the strongest and shortest covalent bonds?

• How easily will a molecule ionize an electron out of a strong covalent bond?

• Based on band gap energy, which structure is the most likely to be an insulator? Does that make sense based on the strength of the bonds?

• Which structure is most likely to display the “sea of electrons” model of bonding?

• Based on band gap energy, which structure is the most likely to be a conductor (metal)?

• Which structure(s) are the most likely to be semiconductors?

• The trend in band gap energy can be qualitatively predicted based on interatomic distance. What is the relationship?

• What happens to the wavelength of the emission as the band gap decreases?

  Increases Decreases

Tuning the Band Gap

The band gap energy can be tuned by varying the chemical composition of the semiconductor. This is important to control the LED color.

The diamond unit cell contains all atoms of the same element arranged in a tetrahedral geometry. Many complementary pairs of atoms that are isoelectronic with diamond have the zinc blende structure.

In zinc blende, sulfide ions, S^-2, are face-centered cubic.

• Draw in zinc cations into tetrahedral holes of the diagram below based on an empirical formula of ZnS.

• How many of the holes are filled?

  

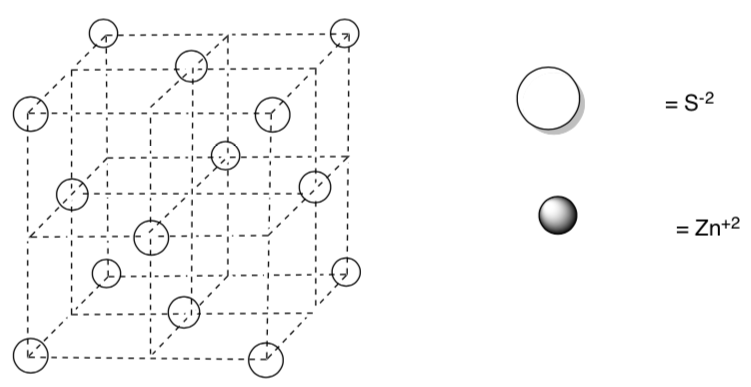
• How does this structure compare to the structure of diamond?

Properties of Materials that are isoelectronic to diamond

Material	Unit Cell Edge Length (Å)	ΔEN	Band Gap Energy (eV)	Emission Walength (nm)
Ge	5.66	0.0	.66	1900
GaAs	5.65	0.4	1.4	890
ZnSe	5.67	0.8	2.7	460
CuBr	5.69	0.9	2.9	430

• As Δ EN increases, the ionic character of the bonds

  Increases or Decreases

• As Δ EN increases, band gap energy

  Increases or Decreases

GaAs and GaP are both solids with the same crystal structure and similar chemistry that can be semiconductors with different band gaps.

• Compare the radii of P vs As. Which is bigger?

• Compare the EN of P vs As. Which is more EN?

• Predict whether GaAs or GaP will have a larger band gap.

• Predict whether GaAs or GaP will produce light with a longer wavelength.

Gallium arsenide phosphide (GaAs1-xPx) is a semiconductor material, a solid solution of GaAs and GaP. It exists in various composition ratios indicated in its formula by the fraction x.

• How do you think the wavelength of light produced by GaAs_0.5P_0.5 will compare to the wavelength from GaAs and GaP?

Application Problem

1. Match binary semiconductors GaP, GaAs, and GaSb with the band gap energies:

   GaP GaSb GaAs

   2.3 eV 1.4 eV 0.7 eV

2. Whichwillhaveagreaterbandgap:

   AlAs GaAs