13.14: Direction of Proton Transfer
- Page ID
- 140115
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Bronsted-Lowry acidity is a special case of Lewis acidity. In Lewis acidity, an electron donor shares electrons with an electron acceptor, forming a bond. In some cases, the electron acceptor is a proton.
If the proton accepts electrons from the donor, but does not relinquish its bond to its previous partner, the interaction is called a hydrogen bond.
If the proton exchanges a new bond with the donor for an old bond with its previous partner -- if it releases a pair of electrons to its partned as it accepts a pair of electrons from the new donor -- the event is called proton transfer.
The compound that provided the proton is called a Bronsted-Lowry acid. The compound that donated the new bond to the proton is called the Bronsted-Lowry base.
Because the proton allowed its former partner to take the pair of electrons from their former bond, that partner becomes a Lewis base. In a proton transfer, the proton moves from one Lewis base to another. The proton could conceivably move back to its original partner, however. The original partner could simply donate its pair of electrons to the proton again. It would displace the new partner and win the proton back.
This situation is called reversibility. Reactions can often move back and forth. In order to convey this idea, when illustrating or writing about these reactions, a pair of opposing arrows are used to show that the reaction can go from left to right as written, as well as from right to left.
- In a reversible reaction, the change that occurs in the reaction can be undone. The reaction can move forwards and backwards.
In most cases, the reaction settles out on one side or the other. Either the reaction goes mostly forward or it goes mostly backward. The point where the reaction settles is termed the equilibrium. At equilibrium, the reactants that come together may mostly be converted into new products. Looking at an equation or diagram of the reaction, , the equilibrium is said to "lie to the right", because the products of the reaction are usually written on the right hand side of the reaction arrow or equilibrium arrow. Some reactions "lie to the left", meaning very little of the original reactants are ultimately converted to the products show.
- The equilibrium is the balance established between the products formed and the original reactants in a reversible reaction.
In a proton transfer, the equilibrium is determined by how tightly the proton is held by each Bronsted acid. The proton will simply remain bonded to whichever compound binds it more tightly. If the difference in binding is great, the equilibrium will lie far to the left or far to the right. If the difference in proton binding is small, there will be a mixture, in which the proton could be in either position.
Remember, most reactions involve zillions of molecules. There is plenty of room for mixtures.
We can predict where the proton will end up by looking at pKas.
- A higher pKa means the proton is more tightly held.
- By comparing the pKa's of the Bronsted acids on both sides of the equation, we can determine which compound will retain the proton.
- The equilibrium will lie towards the compound with the higher pKa.
This idea is illustrated in the equilibrium between hydronium ion and ammonium ion.
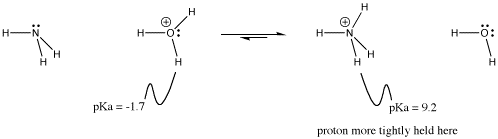
Figure AB14.1. Direction of proton transfer between hydronium and ammonium ion.
As another example, if hydrogen chloride is dissolved in water, the HCl may give up its proton to the water. Water has a lone pair and can act as a base. However, in doing so, the water will form hydronium ion, H3O+. Hydronium ion is Bronsted acidic and can provide a proton to something else that has a lone pair, such as a chloride ion. This reaction could go back and forth. Where will it settle out?
HCl has a pKa of -8. Hydronium ion has a pKa of 0. The equilibrium in the reaction described above lies to the right, towards the hydronium ion produced when the hydrogen chloride dissociates. The proton will remain on the oxygen.
Problem AB14.1.
Write an equation for the proton transfer reactions that could happen in each of the following mixtures. Use structures in your equations. Predict the position of the equilibrium in each case.
a) HF plus water b) CH3CO2H plus ammonia
c) phenol (C6H5OH) plus sodium carbonate d) HCN plus acetonitrile
Problem AB14.2.
Use curved arrows to show the proton transfer reaction between the following compounds.
Predict the products for these proton transfer reactions.
Use pKa to determine whether each reaction is reactant favored OR mixture OR product favored.