13.11: Factors affecting Bronsted-Lowry Acidity: Local Factors
- Page ID
- 140112
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A Bronsted Acid provides a proton to an electron donor. In doing so, the former Bronsted acid becomes a conjugate base. We can understand a great deal about proton transfer by looking at that conjugate base. If the conjugate base is not very stable, then probably the proton will not be donated. If the conjugate base is very stable, then the proton may be given up more easily.
Electronegativity & Nuclear Charge
The first factor to consider is that atom attached to the proton in the Bronsted acid. That is the atom that will accept a pair of electrons from the covalent bond it shares with the proton. How easily can this atom accept a pair of electrons?
An obvious factor to consider is electronegativity. As the atom attached to the proton becomes more electronegative, the bonding pair of electrons becomes more strongly attracted to that atom, and less attracted to the proton. If the bond becomes more polarized away from the proton, it seems likely that the proton will more easily ionize. The molecule containing this bond will be a stronger Bronsted acid. It will not hold onto the proton as tightly. It will have a lower pKa.
Atoms with higher electronegativities are to the upper right in the periodic table. Moving to the right across a row, the nuclear core charge is increasing, so there is more attraction for electrons.
In addition, we should think about what happens after the proton has ionized. In most cases, a neutral (uncharged) Bronsted acid will give rise to an anionic conjugate base. Proton transfer is generally reversible, so it could always go back where it came from, unless something stabilizes the anion that forms. However, if an atom has a higher nuclear core charge, it will be more stable as an anion than would other atoms. That means a compound with a hydrogen attached to that atom will give up a proton more easily. When we consider anion stabilities, the trend across a row of the periodic table is exactly the same as the trend in bond polarity.
Figure AB11.1. Variation in Bronsted acidity across a row in the periodic table.
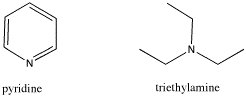
We can compare the pKa's of methane (CH4), ammonia (NH3), water (H2O) and hydrogen fluoride (HF) to examine these ideas. Carbon, nitrogen, oxygen and fluorine are all in a row in the periodic table. Fluorine, to the right, has the highest core charge and highest electronegativity. Carbon, to the left, has the lowest. Water should be a stronger acid than ammonia, which should be more acidic than methane.
In fact, the pKa of hydrogen fluoride is 4; that of water is 14; that of ammonia is 35; and methane's is about 50. Water is much more acidic than ammonia, which is much more acidic than methane. Hydroxide is a more stable ion than amide ion, NH2-, which is a more stable ion than methyl ion, CH3-.
- Electronegativity can reliably be used to compare acidities of two different X-H bonds in the same row.
- The higher the electronegativity of an atom, the more easily its X-H bond ionizes.
- Also, the higher the core charge of an atom, the more stable it will be as an anion, X-, after the proton is lost.
Clearly, none of the compounds illustrated above is highly acidic. If you have learned any chemistry before, you may be familiar with the idea that hydroxide ion is a strong base. Hydroxide has a very strong attraction for protons. It binds a proton to form water, and is much more stable in that form.
However, these comparisons are relative. Amide ion is an even stronger base than hydroxide ion; it binds protons very tightly. Methyl anion is an extremely strong base that binds protons extremely tightly.
Problem AB11.1.
In each case, choose the compound more likely to act as a proton donor.
a) H2S or SiH4 b) GaH3 or AsH3
c) PH3 or AlH3 d) H2Se or HBr
Charge on the proton donor
The atom attached to the proton influences the acidity in other ways. Whether or not that atom has a formal charge becomes very important. The reason is simple: when a proton is given up, the proton will have a positive charge, and the atom releasing the proton will become more negative. Consequently, if the atom attached to the proton already has a negative charge, it is less likely to give up the proton. If it did, it would take on a charge of 2-. That charge build-up would not be very favourable.
On the other hand, if the same kind of atom had a positive charge, it would be much more likely to give up a proton. Once it did, it would have no charge at all. That would be pretty favourable; no energy would have to be expended in stabilizing a charge that is no longer there.
As an example, consider three related species: water (H2O), hydroxide ion (HO-), and hydronium ion (H3O+). Of the three, the hydronium ion would be the most likely to donate a proton, in order to relieve the oxygen atom of positive charge. Charge stabilisation costs energy, so having no charge at all is often better than having a charge.
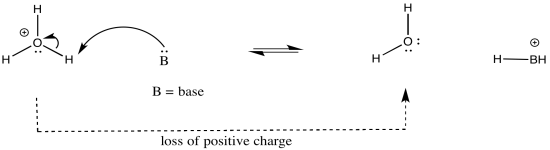
The hydroxide ion would be least likely to give up a proton, because that would leave an oxide ion with a charge of 2-. That increase in negative charge on one atom costs energy.
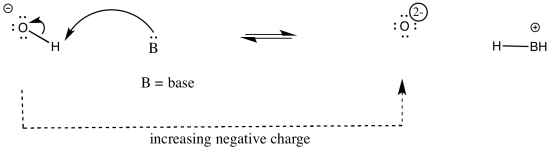
The water ion would be intermediate. There would be an increase in charge on the atom, but it wouldn't be the same as a build up of a 2- charge on the atom.
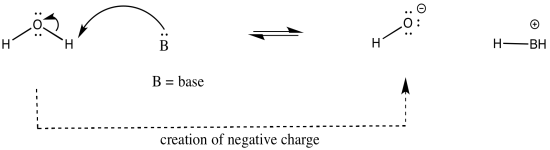
In other words, hydronium ion is more acidic than water, and water is more acidic than hydroxide ion.
Of course, these general rules about acidity do not always apply in different situations. We know that halogens tend to be pretty stable as anions, for the most part, so their anionic form may be more stable than their neutral form. Conversely, positive metal ions may be more stable than the corresponding neutral atom. In the specific case of how likely an atom is to give up a proton, however, the development of charge or loss of charge does become an important factor. This factor is especially important when we are comparing two atoms of the same type, such as two oxygen atoms or two nitrogen atoms.
Problem AB11.2.
In each case, assess whether a formal charge is present. Choose the compound more likely to act as a proton donor.
a) NH4+ or NH3 b) PH2- or PH3 c) H2O or NH4+ d) H3O+ or CH4
Polarizability
Let's look at another example, comparing the pKa's of hydrogen halides. These compounds are all much stronger acids than water. Hydrogen fluoride, HF, has a pKa of 4. Hydrogen chloride, HCl, has a pKa of -1. Hydrogen bromide, HBr, has a pKa of -5, and hydrogen iodide, HI, has a pKa of -7.
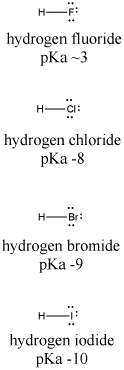
Figure AB11.2. Variation in Bronsted acidity down a column in the periodic table.
Fluoride has the highest electronegativity of the four conjugate bases here, and iodide has the lowest. However, fluoride binds its proton most strongly, and HF has the highest pKa. Something other than electronegativity is at work here.
-
Electronegativity differences cannot explain the differences in acidity of H-X bonds in a column of the periodic table.
One way of discussing this trend is in terms of polarizability. A polarizable atom is generally a large atom that can distribute charge easily over a greater volume; charge is less concentrated than it would be in a smaller atom. The distribution of charge is stabilizing.
-
When comparing anionic atoms from the same column of the periodic table, the polarizability of the atom (related to its size) can be used to explain different anion stabilities.
The reason polarizability dominates comparisons within a column, but not within a row, has to due with the relatively large change in size of atoms from one row to the next. As electrons occupy an additional energy level, the size of the atom increases greatly. Atoms also change size as we move across a row of the periodic table, getting a little smaller as the nuclear charge increases. However, this change is not as dramatic as the change in size from one row to the next.
Earlier, we looked at both sides of the equation, before and after ionization, in terms of core charge and electronegativity. Both considerations led to similar conclusions about which bonds would be most acidic. So far, we have looked at the anions formed when hydrogen halides ionize. Is there a factor (other than electronegativity) we can use in comparing the hydrogen halides directly?
Among these compounds, the bond strength increases from the bottom of the column to the top (from about 70 kcal/mol in HI to about 135 kcal/mol in HF). That means it is much easier to break a hydrogen atom away from an iodine atom in HI than to break a hydrogen atom away from a fluorine atom in HF. That isn't what we are doing when we ionize these bonds; we are breaking a proton away from an anion in each case, rather than a neutral hydrogen atom away from another neutral atom. Nevertheless, whatever factors influence bond strength may be affecting acidity as well.
Bond strengths actually vary in this way indirectly because of the relative electronegativities of the halogens. The valence electrons on fluorine, a more electronegative atom, are at a lower energy than those on either bromine or chlorine. When the valence electrons on a hydrogen atom and a halogen atom combine to form a bond, the bonding combination is at a lower energy than either of the originals.
Of course, the antibonding combination is at a higher energy than either of the originals, but since there are no electrons at that level we don't have to worry about that.
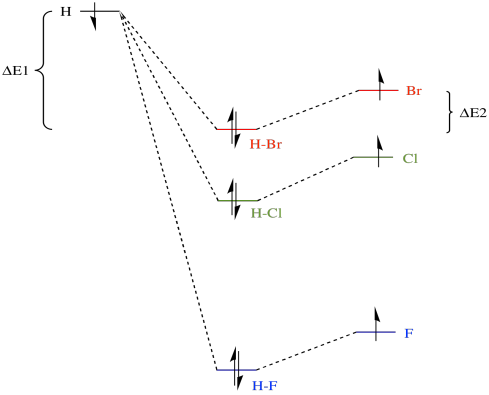
What is a bond strength? It's just the amount of stabilisation upon formation of the bond. Put in an allegorical way, it's how deep the gully is that the electrons have rolled into when the bond forms. To break the bond, the electrons would have to climb the hills back out of the gully again. For example, the bond strength of HBr involves the amount of energy by which the electron on hydrogen has fallen, ΔE1, plus the amount by which the hydrogen on bromine has fallen, ΔE2. To break the bond again, we would have to add in the sum of ΔE1 + ΔE2.
The analogous amount for HCl is greater, mostly because ΔE1 in that case is much larger, and it is even greater for HF. Thus, bond strengths vary in the order HF > HCl > HBr.
While we are looking at that picture, it's worth considering another common aspect of bond strengths. As a simple approximation, there are two important components that describe a bond. One component is overlap (how well the eletrons are shared; that is, how covalent is the bond). The other component is exchange (how much electrostatic attraction there is between the atoms; that is, how polar is the bond). In fact, bromine is better at sharing its electrons with hydrogen than is fluorine, but the H-F bond is more polar than the H-Br bond. The latter fact is another consequence of fluorine's electronegativity. Once again, the greater electronegativity of fluorine actually leads to a stronger bond in this case.
-
In comparing two atoms in a column of the periodic table, bond strength with hydrogen is a good index of how acidic the bond will be.
Note that bond strength does not work as a comparison of H-X bonds in a row of the periodic table. An HF bond is stronger than an OH bond (about 110 kcal/mol) or CH bond (about 100 kcal/mol on average), yet it is much more acidic.
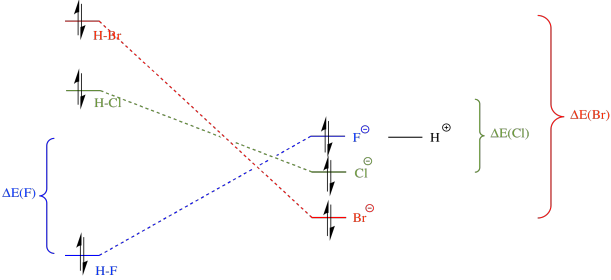
Now, in summary, we need to think about both sides of the equation. The H-F bond is the strongest; that is, it is lowest in energy. However, upon ionisation, bromide is the most stable anion, because it is the largest and most polarisable. Overall, the reaction from HBr to bromide is the most downhill in energy; that one will happen most easily. In contrast, the reaction from HF to fluoride is actually uphill in energy; that one will be most difficult to ionise.
Problem AB11.3.
In each case, choose the compound more likely to act as a proton donor.
a) H2S or H2Te b) GeH4 or SnH4 c) HCl or HBr d) NH3 or AsH3
Problem AB11.4.
Rank the following groups of compounds from most acidic to least acidic.
a) PH3, NH3, AsH3 b) PH3, H2S, SiH4, HCl c) BH3, SiH4, SeH2, HI
Problem AB11.5.
The relative acidities of compounds in some of the following pairs can be explained by polarizabilty. In others, they cannot. Explain why polarizability is or is not a useful comparison to make in each case.
a) CH3OH, (CH3)2CHOH b) SH2, SeH2 c) GeH4, SiH4 d) GeH4, GaH3
Hybridization
There is a special case related to the electron affinity factor described above. It generally shows up in discussions of carbon or nitrogen compounds, and specifically deals with comparisons of two atoms of the same element having different geometry. For example, the C-H bond involving a tetrahedral carbon is extraordinarily non-acidic (pKa near 50), but a C-H bond involving a linear carbon is much more acidic (pKa of about 25).
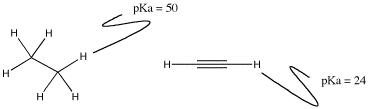
Figure AB11.3. The pKa of protons attached to carbons with tetrahedral and linear geometries.
The argument is sometimes made that this difference results from the molecular orbitals that must be used for formation of the C-H bonds in these complexes. In ethyne, which has linear carbons, bonding to the neighbouring atoms could involve only two atomic orbitals from the carbon, based on geometric considerations. The 2s orbital could contribute to electron sharing; because s orbitals are spherically symmetric, they can bond equally well in all directions. One of the 2p orbitals could also contribute. However, the other two p orbitals cannot be involved, because they are both perpendicular to the first p orbital. If one p orbital lies along the C-H bond axis, the other two are completely orthogonal to it. For that reason, a linear carbon is sometimes called an sp carbon, describing the atomic orbitals that can participate in sigma bond formation with neighbours that lie along a straight line.
The energy of the electrons in this bonding situation will be an average of the energy of an s electron and a p electron. In terms of carbon's energetic contribution, the energy of the electrons in the C-H bond will be halfway between what would be expected if the bond formed between an H atom and a carbon 2s electron and if the bond formed between an H atom and a carbon p orbital. That is because the energy should be an average of the energies of two orbitals that could contribute to that bond.

Figure AB11.4. "Hybrid" energies in bonds involving linear and tetrahedral carbons.
In ethane, which has tetrahedral carbons, a similar argument is made. The difference is that a tetrahedron is a three-dimensional shape. The s orbital can still bond to neighbours in any direction because of its spherical symmetry. However, in order to bond with neighbours in all three dimensions, the entire set of p orbitals would be needed, because each p orbital lies along one dimension only.
The energy of the electrons in this bonding situation will be an average of the energy of an s electron and three p electrons. In terms of carbon's energetic contribution, the energy of the electrons in the C-H bond will be three-quarters of the way between what would be expected if the bond formed between an H atom and a carbon 2s electron and if the bond formed between an H atom and a carbon p orbital. That is because the energy should be an average of the energies of all four orbitals that could contribute to that bond.
Because s electrons are lower in energy than p electrons, the energy of the (s + p) combination will be lower than the energy of the (s + p + p + p) combination. An electron in an "sp orbital" at linear carbon is lower in energy than an electron in the "sp3 orbital" at tetrahedral carbon. If the electron is at lower energy on a linear carbon than a tetrahedral carbon, then a linear carbon has a higher electron affinity than a tetrahedral one.
This comparison is much like the comparison of electron affinity on an oxygen vs a carbon. Oxygen, with a higher electron affinity, generally forms more stable anion than does carbon. An O-H bond is thus more acidic than a C-H bond. A liner C-H bond is more acidic than a tetrahedral C-H bond.
Problem AB11.6.
Predict which of these two nitrogen compounds will be more basic.