12.13: Building MO from Smaller Pieces
- Page ID
- 140075
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Sometimes, compounds are complicated enough that it can be easier to think about the bonding in one portion of the molecule at a time. Ethane, for example, does not contain one central atom like methane does. It contains two atoms that we would think of as being tetrahedral. That makes the potential orbital interactions slightly harder to think about.
That doesn't mean this calculation poses any problem for a computational chemist. A quantitative molecular orbital approach on a computer would begin with a spreadsheet of data to submit for calculations. This data would include a list of all the atoms in the structure and the approximate position of each atom in three-dimensional space. These positions could be thought of in Cartesian coordinates (x,y,z), polar coordinates (r,q ,f ) or internal coordinates (a slightly complicated system relating the relative positions of the atoms with respect to each other: atom B is x distance from atom A; atom C is y distance from atom B and A-B-C forms an angle of z degrees, and so on). The computer does not need to know where the bonds are or where the electrons are; it will figure that out from its calculations. Ethane would prove to be very simple to calculate with a computer.
On paper, we might need to break ethane down into easier pieces. The obvious thing to do is break ethane into two smaller parts and then bring those parts together. Ethane could easily be thought of as two CH3 units interacting together.
The geometry of a CH3 unit may be debatable. Since we expect the carbon to be tetrahedral in ethane, it is probably easiest to think of CH3 as pyramidal, in terms of the relationship of the four atoms. The three hydrogens form a triangle at the base of the pyramid, with the carbon at the apex of the pyramid.
Now we have two methyl groups. We can bring them both together and allow the previously non-bonding orbitals to interact with each other.
- If we take a hybrid approach to the methyl group, we can use the 2s orbital and all three 2p orbitals to bond with the hydrogens.
- There are only three hydrogens, so we only need three of the sp3 orbital set to bond with the hydrogens.
- There will be three bonding combinations using these orbitals and three antibonding combinations.
- These interactions describe the C-H bonds.
- The last of the sp3 set will be left non-bonding. We don't care which orbital this is because we are taking a shortcut.
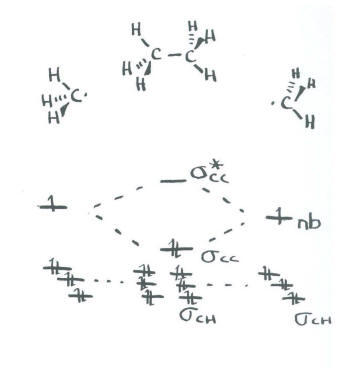
- The remaining orbital from the sp3 set on one methyl interacts with the remaining orbital from the sp3 set on the other methyl.
- There is a bonding and an antibonding combination.
- This interaction describes the C-C bond.
- The C-C bond is probably not at the same energy level as the C-H bonds.
- We know from experiment that C-C bonds are weaker than C-H bonds, so we will place it higher in energy than the C-H bonds.
This approach does not agree well with the exact energy levels of the C-H bonds as determined by both quantitative molecular orbital theory and photoelectron spectroscopy. However, it is a method that will allow us to tackle bigger problems without worrying about some of the details.
Problem MO13.1.
Use the partial structure approach, with a hybridization model, to construct an approximate molecular orbital interaction diagram of ethene, connected CH2-CH2 (two H on the first carbon, two H on the second, the two carbons connected together).
a) Build this model up from two methylene groups, CH2 and CH2. What will be the geometry of each carbon in ethylene?
b) Given that geometry, choose the appropriate set of carbon s & p orbitals to bond to the neighbours. Build the methylene molecular orbital energy level diagram.
c) Bring the two methylenes together. Let an unused orbital from your hybrid set interact with the same kind of orbital from the other methylene.
d) When finished, are there other unused atomic orbitals on each methylene? If so, could they form an additional bond?
Problem MO13.2.
Use the partial structure approach, with a hybridization model, to construct an approximate molecular orbital interaction diagram of ethyne, connected CH-CH (one H on the first carbon, one H on the second, the two carbons connected together).
a) Build this model up from two methyne groups, CH and CH. What will be the geometry of each carbon in ethyne?
b) Given that geometry, choose the appropriate set of carbon s & p orbitals to bond to the neighbours. Build the methyne molecular orbital energy level diagram.
c) Bring the two methynes together. Let an unused orbital from your hybrid set interact with the same kind of orbital from the other methyne.
d) When finished, are there other unused atomic orbitals from each methyne? If so, could they form an additional bond?
Problem MO13.3.
Use the partial structure approach, with a hybridization model, to construct an approximate molecular orbital interaction diagram of formaldehyde, connected CH2-O (two H on the carbon, carbon connected to oxygen).
a) Build this model up from a methylene group, CH2. What will be the geometry of each carbon in ethylene? What set of carbon s & p orbitals will bond to the neighbours? Build the methylene molecular orbital energy level diagram.
b) Bring the methylene with an oxygen. Let an unused orbital from your hybrid set on methylene interact with any orbital you think will overlap with it on the oxygen
d) When finished, are there other unused atomic orbitals on the methylene? If so, could they form an additional bond with any atomic orbital on oxygen?

