12A: Molecular Shapes
- Page ID
- 81612
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Name: ______________________________
Section: _____________________________
Student ID#:__________________________
Work in groups on these problems. You should try to answer the questions without referring to your textbook. If you get stuck, try asking another group for help.
- Understand the basis of the VSEPR theory.
- Know the expected geometries for one through six electron domains about a central atom
- Understand how bond pairs and lone pairs about a central atom interact to produce the molecular shape
- Know how bond polarity and molecular shape combine to make a molecule polar or nonpolar.
Contrary to the impression that Lewis structures may give, many molecules have three-dimensional geometries. These molecular shapes are very important to understanding how molecules interact with each other, both chemically and physically. Although the Lewis structures themselves do not convey shape information, they can be used as the starting point for applying a conceptually simple but powerful approach to predicting molecular geometries. This method is called the Valence Shell Electron Repulsion Theory, or VSEPR for short. Knowing the shape of a molecule enables us to predict whether or not it has an electrical polarity, which is an important property determining how the species interacts with other molecules.
Success Criteria
- Be able to use a Lewis structure and VSEPR theory to predict the shape of molecules
- Be able to sketch the shapes of simple molecules
- Be able to name electron domain and molecular shape geometries of simple molecules
- Be able to predict whether a particular molecule is polar or nonpoloar
Basic Domain Shapes from VSEPR Theory
One of the most successful approaches to predicting the shapes of molecules is based almost solely on considerations of how best to minimize electron-pair repulsions about a central atom. This approach, which was originated by Nyholm and Gillespie in the 1950's, has become known as the Valence Shell Electron Pair Repulsion Theory, or VSEPR. theory. The fundamental premise of this theory can be stated as follows:
Electrons in bonded atoms occupy spatially oriented orbitals in such a way as to minimize electron-electron repulsions arising mainly from electrostatic (coulombic) forces.
The approach is remarkably accurate in predicting the basic shapes of molecules of non-transition elements, although some details of bond angle and bond length are not well explained by electron repulsion alone. At this point we will not be concerned with the identity of the spatially oriented orbitals. However, assuming that such orbitals are available, we can determine for various numbers of pairs of electrons about a central atom the most favorable electron pair geometry to minimize electron-electron repulsions.
To illustrate the approach, let us consider a number of molecules in which all of the valence electrons about the central atom are engaged in bond formation with outer-lying (pendant) atoms. Consider BeCl2, for which the Lewis dot structure is
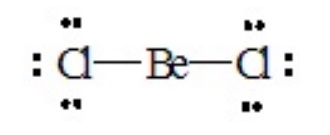
There are two pairs of electrons around the central Be atom. If they are oriented 180o from each other their repulsions will be minimized. Therefore, the best electron pair geometry for two pairs is a linear arrangement. Both pairs are involved in forming single bonds in BeCl2, so the resulting molecular geometry or shape of the molecule is also linear.
Consider BCl3, for which the Lewis dot structure is
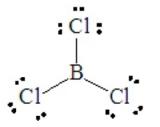
This has three pairs around the central B atom. Electron-pair repulsions are minimized by placing these three pairs at 120o apart in a plane, called a trigonal planar arrangement. All three pairs are involved in bond formation, so the molecular shape is trigonal planar, as a result of the electron pair geometry.
Consider methane, CH4, for which the Lewis dot structure is
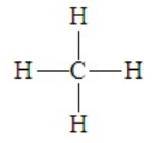
Contrary to what this model seems to suggest, a square planar arrangement of the four pairs about carbon is not the best for minimizing electron repulsions. By assuming the three-dimensional tetrahedral arrangement, the pairs will be in positions 109.5o apart. Thus methane is tetrahedral. Given the prevalence of an octet about a central atom, this electron pair geometry occurs in many compounds. It is a highly symmetrical arrangement in which all four positions are equivalent. When representing this three-dimension structure in a two-dimensional sketch, we often employ drawings such as the following::

The solid lines are positions in the plane of the page. The solid wedge is a position coming out of the plane of the page, and the dotted line is a position going back below the plane of the page. It is important to realize that regardless of the drawing, any position is surrounded by three others, all making an angle of 109.5o to each other. No position is “across from” any other, as could be the case in a square planar arrangement.
Consider PCl5. This is a case of hypervalence, with five pairs of electrons about the central atom. The best electron pair geometry is a trigonal bipyramid.
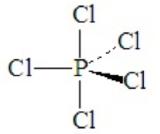
A trigonal bipyramid has two kinds of positions, which are not equivalent to each other. The two axial positions make a 180o angle to each other and a 90o to the plane of the three equatorial positions. The equatorial positions form a 120o angle between each other.
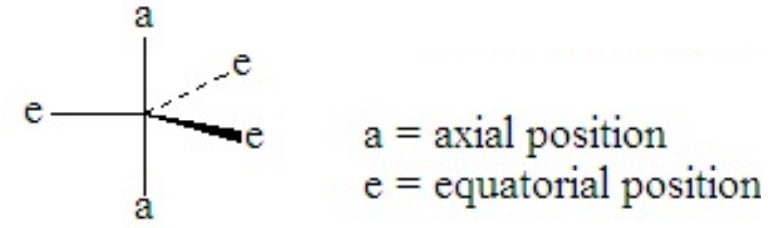.jpg?revision=1&size=bestfit&width=447&height=132)
Consider SF6, a hypervalent molecule with six pairs about the central sulfur atom. The best electron pair geometry is achieved by placing all pairs at 90o to one another, as with the axes of a Cartesian coordinate system. This arrangement is octahedral.
.jpg?revision=1&size=bestfit&width=150&height=159)
Unlike the trigonal bipyramid, all positions in the octahedron are equivalent.
Electron pairs involved in multiple bond formation occupy the same region of space. Therefore, all pairs in a double or triple bond function in the same way as a single pair in determining geometry. For this reason, we should look at the number of electron domains about the central atom, rather than the number of electron pairs, particularly when multiple bonds are involved. For example, formaldehyde, H2CO, has the following Lewis structure, with three electron domains around the central atom
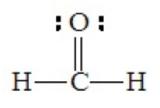
Although there are four pairs about the central carbon atom, they are grouped into only three domains, two for single C–H bonds and a third for the C=O bond. The best arrangement to minimize repulsions is trigonal planar.

All bond angles will not be perfectly 120o. The larger oxygen atom forces the two hydrogen atoms together slightly, so that the H-C-H angle is somewhat less than 120o.
Similarly, HCN is a linear molecule because the four pairs around the central carbon atom are arranged in two domains:
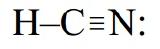
The shapes of molecules that are resonance hybrids can be deduced from any one of the hypothetical resonance forms. For example, any one of the three principal resonance forms of the nitrate ion shows four pairs around the central nitrogen atom arranged in three domains:
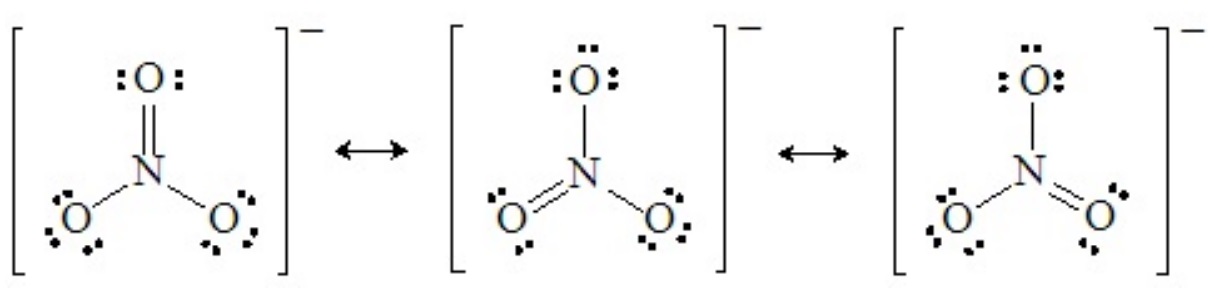
Recall that in resonance forms like these, there are no real double bonds, and all the N–O bonds are equivalent (bond order of 4/3). Therefore, the structure of the nitrate ion is truly trigonal planar, with 120o O–N–O angles.
Q1
Give the names for the shapes of the domain geometries for two through six regions of electron density about a central atom.
Q2
Draw Lewis structures for the following molecules, and predict the the shapes on the basis of VSEPR considerations: SnH4, CO2, AsF5, Cl2CO.
Shapes of Molecules with Lone Pairs
In many molecules some pairs of valence electrons around the central atom may be non-bonding lone pairs. In these cases, the electron domain arrangements will be the same for the total number of electron pairs, but the molecular shape will be different. Keep in mind that the shape of a molecule refers to the geometrical arrangement of its atoms, not the domain geometry of its electron pairs. However, the resulting shape for molecules with lone pairs on the central atom will be based on the electron domain geometries we have just seen. Bond angles in these molecules will often deviate from the ideal angles of the electron domain geometries. This is the result of differences in the strengths of repulsions between electrons involved in bond formation and those that are not. In general, the strengths of electron pair repulsions decline in the order
lone pair - lone pair > lone pair - bond pair > bond pair - bond pair
When adding lone pairs in electron domain geometries in which all positions are equivalent the arrangement that clearly minimizes lone pair - lone pair repulsion results. We will not go through every possible shape here, but the case of NH3 serves to illustrate the effects of lone pair - bond pair repulsions on the resulting shape. The Lewis dot structure is shown below:
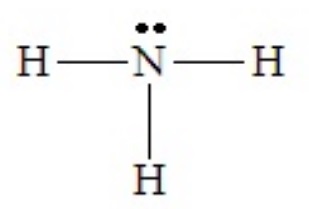
With four domains about the central N atom, the electron domain geometry is tetrahedral. But the shape of the molecule cannot be described as tetrahedral, because there are only three bonds. The combination of three bond pairs and one lone pair (3 bond pairs + 1 lone pairs) results in a tripod-like arrangement of the atoms, called a trigonal pyramid.
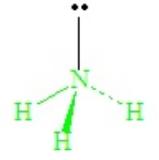
The lone-pair - bond-pair repulsions, being stronger than bond-pair repulsions, cause all H—N—H angles to close down from the ideal 109.5o of the tetrahedron, becoming ~107o in ammonia.
Cases involving five domains about a central atom require some care in placing any lone pairs. Such hypervalent structures are all based on a trigonal bipyramidal (tbp) geometry of the electron domains. But as we previously noted, there are two kinds of positions for tbp: axial and equatorial. For most cases in which the central atom is a main-group element, the axial positions are somewhat longer than the equatorial positions. A lone pair is associated with only one nucleus, whereas a bond pair is associated with two. Therefore, in structures based on a tbp domain geometry, any lone pair will be closer to the one nucleus with which it is associated if it is in one of the shorter equatorial positions. Therefore, when building shapes based on a tbp domain geometry, always place the lone pairs in the equatorial positions.
SF4 illustrates the effect on shape of placing a lone pair in an equatorial position of a tbp domain geometry. Without careful consideration, SF4 might seem to be a tetrahedral molecule, but as the Lewis dot structure shows it is a hypervalent case with five electron domains.
.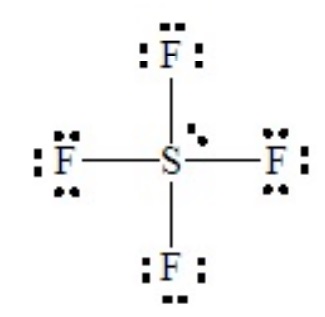
This is a case of 4 bond pairs + 1 lone pairs Placing the lone pair in an equatorial position results in the following molecular shape, with the orientation of the molecule flipped in the second sketch:
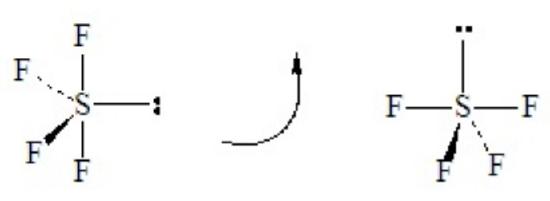
When flipped, as shown on the right, the shape resembles a playground “see-saw” with the two equatorial-type positions functioning as the fulcrum and the two axial-type positions forming the plank. The official name of this is irregular tetrahedron, although mathematicians call the related solid polygon a disphenoid. Note that SF4 has two kinds of bonds with two different lengths: the two axial bonds of the tbp and the two remaining equatorial bonds of the tbp. The lone-pair repulsions cause the angle between the two axial-type bonds to be less than 180o, and cause the angle between the two equatorial-type bonds to be less than 120o.
The table in Appendix A summarizes the expected shapes for all combinations of bond pairs and lone pairs for two through six electron domains (ED). Be sure that you become so familiar with all the possibilities that you do not need to refer to Appendix A or a similar table to determine the shape of a molecule by VSEPR theory.
Another useful way to organize your thinking about molecular geometries is to consider what the possible shapes are for a certain number of pendant atoms attached to a central atom. This helps rule out impossible shapes at the start. The table in Appendix B rearranges the information in Appendix A on the basis of molecular formulas. For example, if a molecule has a formula MX2, the fact that it is composed of only three atoms means that they are either all aligned (linear) or they are not (bent), regardless of the domain geometry that gave rise to the shape. No other shapes are possible. It makes no sense to say that a molecule with a formula MX2 is trigonal planar, tetrahedral, or trigonal bipyramidal just because we can identify three, four, or five domains about the central M atom. The first two cases would be bent, and the last would be linear. Beyond this, we should expect a X–M–X angle slightly less than 120o if the shape is based on three domains, and slightly less than 109.5o if based on four domains.
Q3
For each of the following molecules or ions, sketch the shape and name it. You should start with a valid Lewis structure in each case, before applying VSEPR considerations: SeCl4, I3–, PSCl3, IF4–, IF4+, PH2–, N3–, PH4–
Q4
Describe the structure and bonding of the nitrite ion, \(NO_2^–\).
Molecular Polarity and Dipole Moments
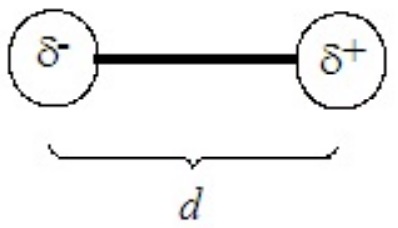
The polarity of a molecule is measured as its dipole moment, defined as
\[μ = δd \nonumber \]
where μ is the dipole moment, δ is the charge on each end of the molecule (δ+ and δ–), separated across the molecule by a distance d. The units of dipole moment are the debye (D), defined as 3.34 x 10-3 C×m. (C = coulomb)
In a diatomic molecule the charges, which are generally much less than unit charges, reside on the two atoms and d is their internuclear separation (bond length). For a diatomic molecule the model is something like the following:
For heteronuclear diatomic molecules, the bond has polarity, so the molecule will have a dipole moment. Thus, all heteronuclear diatomic molecules are polar. All homonuclear diatomic molecules have no dipole moment. The following data illustrate:
| Molecule | μ | Molecule | μ |
|---|---|---|---|
| H-H | 0 D | H-F | 1.82 D |
| F-F | 0 D | H-Cl | 1.08 D |
| Cl-Cl | 0 D | H-I | 0.44 D |
For polyatomic molecules, polarity depends on both shape and composition. A molecule is nonpolar when all individual bond polarities are counterbalanced by other identical bond polarities. A molecule is polar when any one of its individual bond polarities is not counterbalanced by identical bond polarities. Lack of counter balancing polarities may result from a less symmetrical shape (shape). Lack of counterbalancing polarities also may result from a unique bond in the molecule, having a different bond strength or bonding to a different element (composition).
In highly symmetric binary molecules (two elements), individual bond polarities may cancel, leaving the molecule with no net dipole moment, as in all of the following cases.
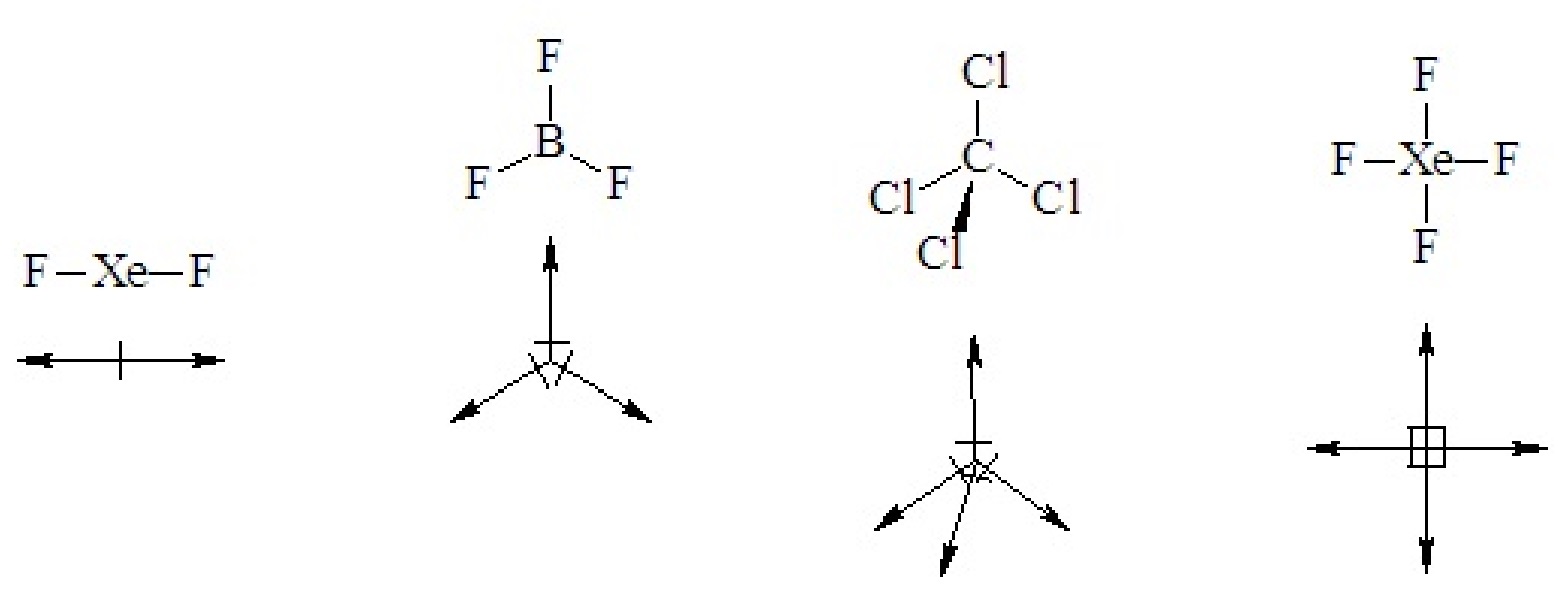
If a binary molecule has a geometry that gives it a sense of up or down or right and left it is polar.
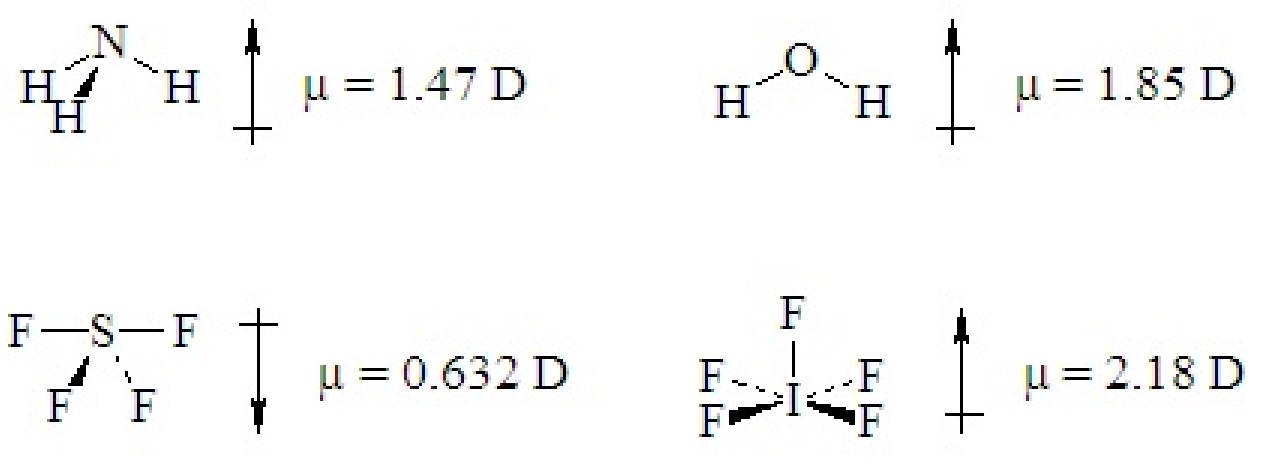
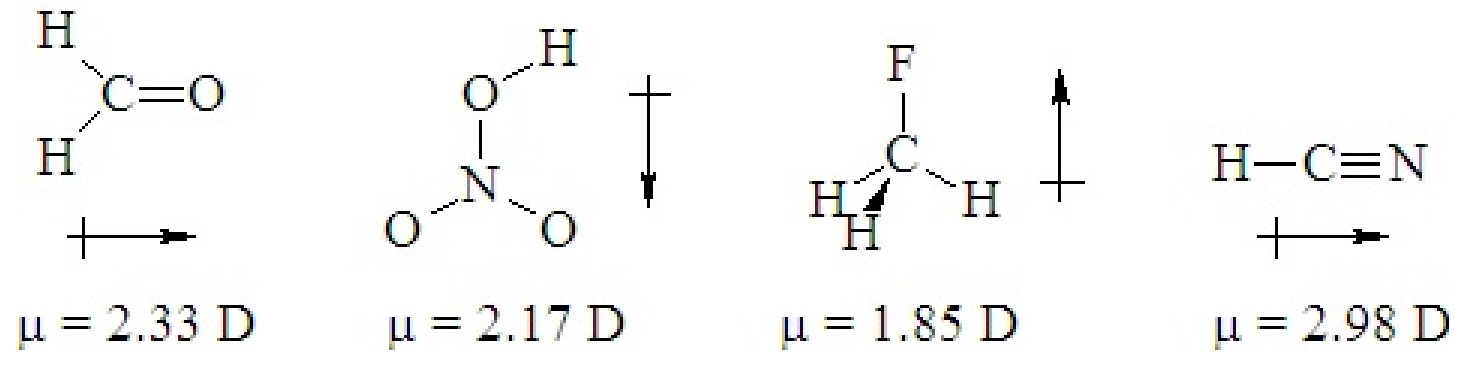
If a ternary molecule has its bonds asymmetrically arranged, it may be polar even though its shape would be nonpolar for a binary molecule. The following cases have shapes that would be nonpolar for binary molecules but which are polar because there are two different kinds of bonds around the central atom that are not symmetrically arranged.
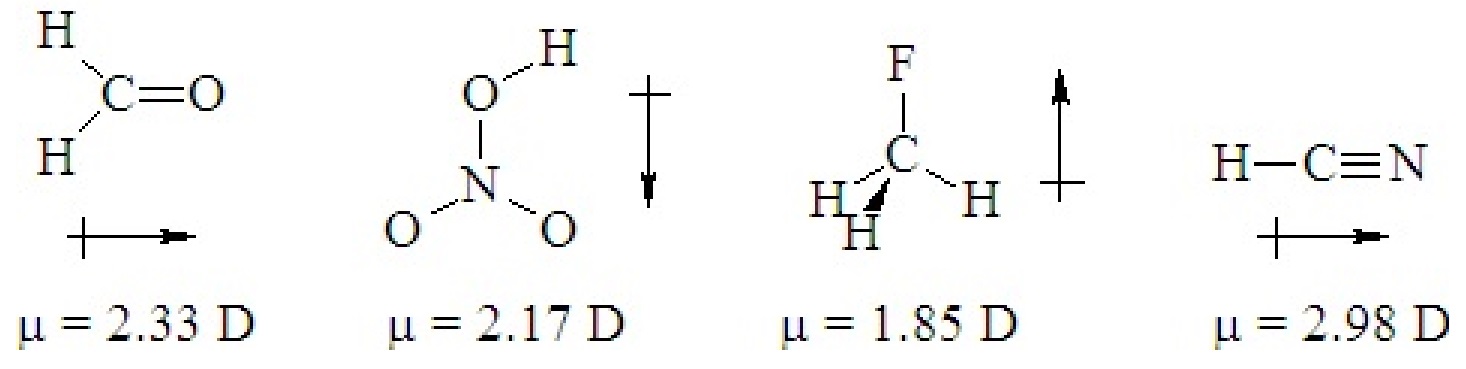
Q5
For all the molecules or ions whose shapes you determined in Q3. indicate whether or not the species is polar.
Q6
Consider the following Lewis structures for some simple organic compounds. (Lone pairs on pendant atoms have been omitted for simplicity.) Redraw each of these on the basis of VSEPR considerations, and indicate whether or not the molecule is polar.
Q7
A certain compound with a formula AB4 is found to be polar. Moreover, it is determined that there are two different bond lengths, two long ones and two short ones. What is the probable shape of the molecule? Explain your reasoning.
Appendix A: Shapes of Molecules for Various Electron Domain (ED) Geometries
| ED | Domain Geometry | Bond Domains | Lone Pairs | Molecular Shape | Examples |
|---|---|---|---|---|---|
| 2 | linear | 2 | 0 | linear MX2 | BeF2, CO2 |
| 3 | trigonal planar | 3 | 0 | trigonal planar MX3 | BF3, NO3– |
| 2 | 1 | bent MX2 (<120o) | SnCl2, NO2– | ||
| 4 | tetrahedral | 4 | 0 | tetrahedral MX4 | CH4 |
| 3 | 1 | trigonal pyramidal MX3 | NH3 | ||
| 2 | 2 | bent MX2 (<109.5o) | H2O | ||
| 5 | trigonal bipyramidal | 5 | 0 | trigonal bipyramidal MX5 | PCl5 |
| 4 | 1 | irregular tetrahedron MX4 | SF4 | ||
| 3 | 2 | T-shaped MX3 | ClF3 | ||
| 2 | 3 | linear MX2 | XeF2 | ||
| 6 | octahedral | 6 | 0 | octahedral MX6 | SF6 |
| 5 | 1 | square pyramid MX5 | IF5 | ||
| 4 | 2 | square planar MX4 | XeF4 |
Note: In this table, “bond” means a linkage between two atoms in a molecule. Thus, a single-, double-, or triple-bond constitutes only one bond.
Appendix B: Possible Shapes of Molecules with Formulas MXn, n = 2 – 6
| Formula | Case | Shape | Example |
|---|---|---|---|
| MX2 | 2 bonds + 0 lone pairs | linear | BeF2 |
| 2 bonds + 1 lone pair | bent (<120o) | SnCl2 | |
| 2 bonds + 2 lone pairs | bent (<109.5o) | H2O | |
| 2 bonds + 3 lone pairs | linear | XeF2 | |
| MX3 | 3 bonds + 0 lone pairs | trigonal planar | BF3 |
| 3 bonds + 1 lone pair | trigonal pyramidal | NH3 | |
| 3 bonds + 2 lone pairs | T-shape | ClF3 | |
| MX4 | 4 bonds + 0 lone pairs | tetrahedral | CH4 |
| 4 bonds + 1 lone pair | irregular tetrahedron | SF4 | |
| 4 bonds + 2 lone pairs | square planar | XeF4 | |
| MX5 | 5 bonds + 0 lone pairs | trigonal bipyramid (tbp) | PF5 |
| 5 bonds + 1 lone pair | square pyramid | IF5 | |
| MX6 | 6 bonds + 0 lone pairs | octahedral | SF6 |
Note: In this table, “bond” means a linkage between two atoms in a molecule. Thus, a single-, double-, or triple-bond constitutes only one bond.


