11A: Chemical Bonds

Name: ______________________________

Section: _____________________________

Student ID#:__________________________

Work in groups on these problems. You should try to answer the questions without referring to your textbook. If you get stuck, try asking another group for help.

A chemical bond exists between any two atoms that are strongly attracted to one another in a compound or element. Ionic compounds are held together mainly by electrostatic forces of attraction between the oppositely charged ions, creating ionic bonding. Atoms in nonmetallic elements and molecular compounds are held together by sharing of electrons, creating covalent bonding. When a compound consists of molecules with covalent bonds, a Lewis model is often a simple way of representing its bonding. Ionic and covalent bonding represent extreme models, with most real bonds lying somewhere in between. Any bond between two different elements involves an inequality of electron sharing, which creates bond polarity and a certain degree of ionic character. One way of assessing the ionic or covalent character of a bond is the difference in electronegativity between the two bonded atoms.^[1]

Learning Objective

• Understand the distinction between ionic and covalent bonding
• Understand the electronegativity scale and its use for assessing bond type
• Understand the concept of lattice energy as a measure of bonding strength in ionic compounds
• Understand the concept of covalent bonding in terms of the Lewis model

Success Criteria

• Be able to describe the character of a bond on the basis of electronegativity differences
• Be able to predict relative lattice strengths among ionic compounds
• Be able to draw Lewis dot structures of simple molecular compounds
• Be able to assign formal charges in a Lewis structure and use these to assess relative reasonableness of the model
• Be able to write resonance forms where appropriate and be able to assess relative bond strength in molecules represented by resonance forms.

Bond Type and Electronegativity

An ionic bond is formed by electrostatic forces of attraction between ions. For example, \(\ce{NaCl}\) is composed of \(\ce{Na^{+}}\) ions and \(\ce{Cl^{–}}\) ions in a cubic array. At the atomic level, we can imagine the formation of these ions through a process in which an electron from an atom of Na is transferred to an atom of \(\ce{Cl}\).

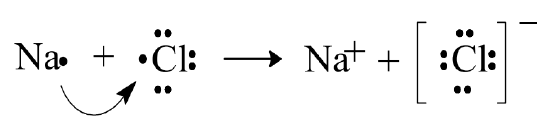
In this representation, the dots around each species indicate the valence electrons. This method of representation is called an electron-dot model or Lewis-dot model (after G. N. Lewis who devised the scheme). The complete transfer of an electron and formation of discrete ions, which this process suggests, would lead to a purely ionic bond. In actuality, complete transfer never occurs in the formation of an ionic compound, and there is always some degree of sharing of electrons between the ion pair. Therefore, the purely ionic bond must be regarded as only a hypothetical extreme model, an approximation in real cases.

At the opposite extreme, a covalent bond is formed by sharing electrons between atoms. If the atoms are identical, a homonuclear bond will result in which the sharing of electron density is equal between the bonded atoms. This constitutes a pure covalent bond. All elements that exist in molecular form have pure covalent bonds between their atoms; e.g., H₂, O₂, N₂, P₄, S₈. If the two atoms are different, a heteronuclear bond will result in which the sharing of electron density is unequal. The atom with the greater attraction for electrons will acquire a greater share of the total electron density, giving it more electron density than it had as an isolated atom. In the bond, this atom will have acquired a partial negative charge, indicated \(δ^{–}\). (δ = lower case Greek delta) The other atom will lose some of its electron density, giving it a partial positive charge, indicated \(δ^{+}\). The unequal sharing of electron density in heteronuclear covalent bonds gives them polarity and partial ionic character.

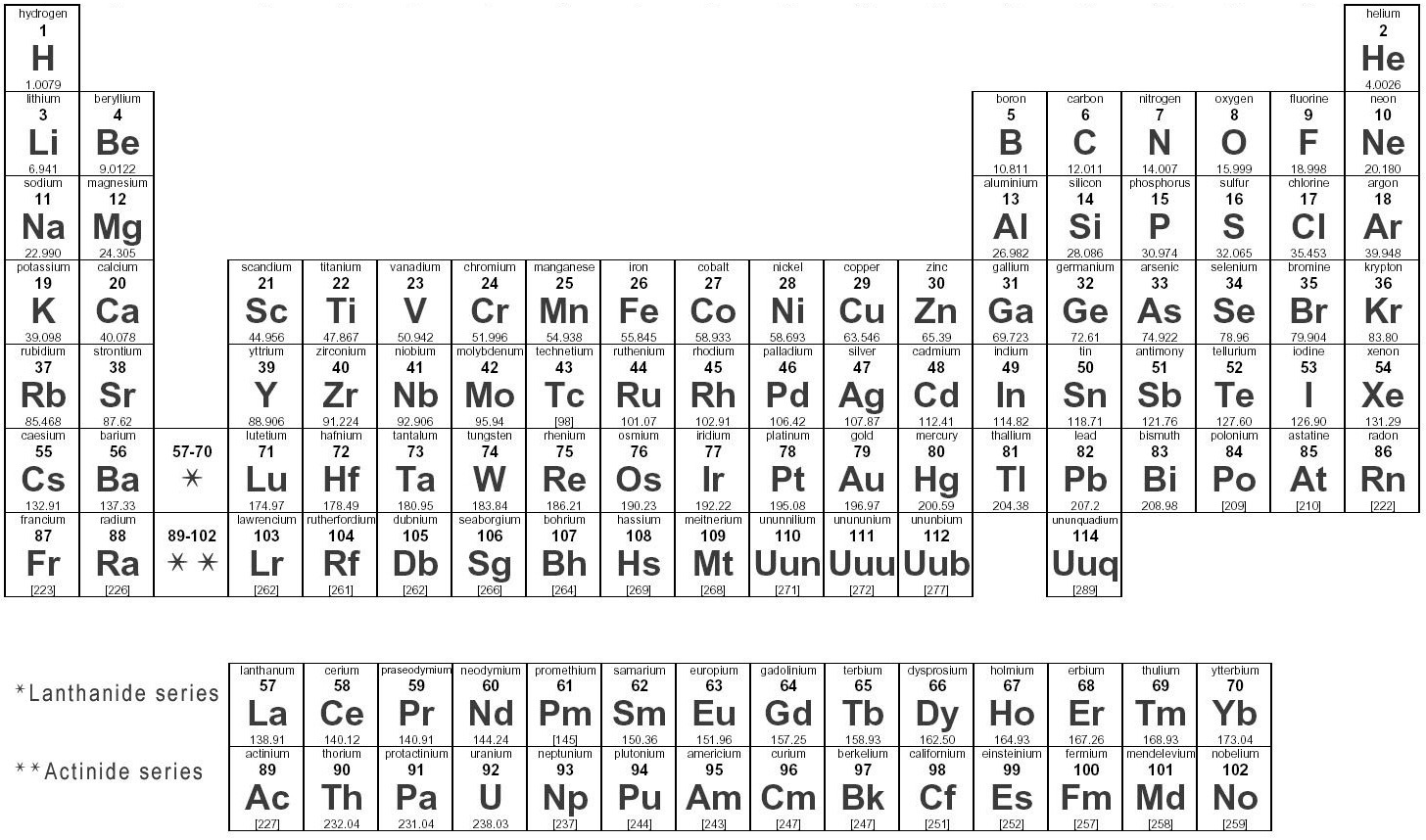
The attraction an atom has for electrons in a chemical bond is called its electronegativity. This is not a directly measurable quantity, and historically there have been several different approaches to estimating it. In the 1930s, Linus Pauling developed a scale of electronegativities that was widely adopted, and that has been modified and improved over the years. On the Pauling scale, values of electronegativity, symbolized by the Greek letter \(\chi\), range from a low of 0.7 for francium to a high of 4.0 for fluorine. This range for the electronegativity scale is arbitrary, because there are no units associated with \(\chi\). (Pauling could have just as easily chosen, say, 10, 100, 72.3, or any other number for the most electronegative value!) Nonetheless, the Pauling range of values has been carried over more or less as the standard for other systems of calculating electronegativity, some of which quote the values to greater precision. The values for each element on the Pauling scale, which we will use, are indicated on the following table.

	1	2											13	14	15	16	17
1	H 2.1
2	Li 1.0	Be 1.5											B 2.0	C 2.5	N 3.0	O 3.5	F 4.0
3	Na 0.9	Mg 1.2	3	4	5	6	7	8	9	10	11	12	Al 1.5	Si 1.8	P 2.1	S 2.5	Cl 3.0
4	K 0.8	Ca 1.0	Sc 1.3	Ti 1.5	V 1.6	Cr 1.6	Mn 1.5	Fe 1.8	Co 1.8	Ni 1.8	Cu 1.9	Zn 1.6	Ga 1.6	Ge 1.8	As 2.0	Se 2.4	Br 2.8
5	Rb 0.8	Sr 1.0	Y 1.2	Zr 1.4	Nb 1.6	Mo 1.8	Tc 1.9	Ru 2.2	Rh 2.2	Pd 2.2	Ag 1.9	Cd 1.7	In 1.7	Sn 1.8	Sb 1.9	Te 2.1	I 2.5
6	Cs 0.7	Ba 0.9	La-Lu 1.1-1.2	Hf 1.3	Ta 1.5	W 1.7	Re 1.9	Os 2.2	Ir 2.2	Pt 2.2	Au 2.4	Hg 1.9	Tl 1.8	Pb 1.8	Bi 1.9	Po 2.0	At 2.2
7	Fr 0.7	Ra 0.9	Ac-No 1.1-1.7

Note that no element has a zero electronegativity, because that would imply no attraction between its nucleus and electrons.

The periodic trends in electronegativity can be summarized by the following statements:

• Electronegativity increases across a period.
• Electronegativity decreases down a group.
• Metals have low electronegativities.
• Nonmetals have high electronegativities.

The absolute value of the difference in electronegativities between two bonded atoms,

\[δ_{\chi} = | \chi_A – \chi_B| \nonumber \]

can be used to estimate how unequal the sharing of electrons is in the bond, and hence how covalent or ionic the bond is. The numbers calculated in this way give an overly simplified view of the electronic environment of a chemical bond, but the qualitative idea behind this approach remains useful. A pure covalent bond (equal sharing), such as exists in a homonuclear bond, has \(δ_{\chi} = 0\), because both atoms in the bond have identical electronegativities. For heteronuclear bonds, where the two atoms have different electronegativities, a small difference in electronegativities indicates a more nearly pure covalent bond. Conversely, the larger the difference in electronegativities the more polar covalent the bond will be. Increasing bond polarity is taken as equivalent to increasing ionic character for the bond. Given the range of electronegativity values, the largest value of δχ occurs for the pair \(\ce{FrF}\), for which

\[δ_{\chi} = | \chi_A – \chi_B| = |0.7 – 4.0| = 3.3. \nonumber \]

This represents the most ionic bond possible. That francium's electronegativity is not zero indicates that it does not totally surrender an electron in forming \(\ce{FrF}\). This is consistent with the point previously made: the ideal of a perfect ionic bond, for which \(δ_{\chi} = 4.0\), does not exist.

There is no precise cut-off point between polar covalent and ionic bonding. Nonetheless, if \(δ_{\chi} \ge 1.7-1.8\), the bond is probably best regarded as ionic. Values of \(δ_{\chi}\) that lie below but near this imprecise border may be regarded as polar covalent; i.e., covalent with an appreciable amount of ionic character. Values of δχ that lie above but near this border may be called ionic, but will have some degree of covalent character, becoming less so as \(δ_{\chi}\) increases. In light of the trends in electronegativity, the most ionic binary compounds can be expected to be formed by combinations of elements in the lower left portion of the periodic table with those in the upper right; i.e., metals and nonmetals. The most covalent of heteronuclear bonds are expected among near-neighbor nonmetallic elements. Only homonuclear bonds between identical atoms in molecules of elements are perfectly covalent.

Difference in electronegativity, taken in isolation, can sometimes mislead about the nature of a bond. While \(δ_{\chi} \ge 1.7-1.8\) may suggest ionic bonding, a compound whose bonds are in this range is probably not ionic if it is a gas or a liquid at ordinary temperatures. Recall that simple ionic compounds are solids at room temperature. Gas or liquid compounds whose bonds are in the range \(δ_{\chi} \ge 1.7-1.8\) usually have very polar covalent bonds, but they are not considered to be ionic. At the other extreme, if a bond between two different elements has δχ = 0, it is not purely covalent. Different elements inherently have different abilities to attract electrons in a chemical bond. When heteronuclear bonds have \(δ_{\chi} = 0\), the difference is so small that the electronegativity scale is simply too imprecise to indicate it. All heteronuclear bonds should be regarded as polar to some extent. If \(δ_{\chi} = 0\) for a heteronuclear bond, it is virtually pure covalent, but not exactly so (requires a more advanced treatment than here to explain).

Q1

Using the electronegativity values in the table above, calculate δχ for the pairs of elements forming bonds in each of the following species, and describe the type of bonding as either pure covalent, polar covalent, or ionic: H₂, HCl, PbBr₂, NaCl, NBr_3.

Q2

Calculate \(δ_{\chi}\) for the bonds in HF(g) and NCl₃(l) and describe them.

Lattice Energy

The measure of the stability of an ionic substance’s crystal lattice is the lattice energy, defined as the enthalpy associated with completely separating one mole of solid ionic compound into its gaseous ions. For \(\ce{NaCl(s)}\) the lattice energy, \(U\), is defined as

\[NaCl(s) \rightarrow Na^+(g) + Cl^–(g) \nonumber \]

wiht \(ΔH^o = U = +788\, kJ\).

This is always an endothermic enthalpy, because breaking up the crystal lattice requires overcoming the attractions between the cations and anions. The higher the attraction between cations and anions, the higher will be the lattice energy. The lattice energy for an ionic compound is not directly measurable. However, the enthalpy of formation for an ionic compound can be measured, and along with data to calculate the enthalpies of formation of the ions, the value of \(U\) can be calculated by applying the Law of Hess in a series of thermochemical equations called the Born-Haber cycle.

Large values of lattice energy, implying a stable crystal lattice, are favored by (a) higher ionic charges, (b) smaller ions, and (c) shorter distances between ions. The following data illustrate these trends for the ionic compounds formed by the indicated pairs of ions.

Figure \(\PageIndex{1}\): Selected Lattice Energies, \(U^o\) (kJ/mol) (Born-Haber Cycle Data)

	F^–	Cl^–	Br^–	I^–	O^2–
Li^+	1049.0	862.0	818.6	762.7	2830
Na^+	927.7	786.8	751.8	703	2650
K^+	825.9	716.8	688.6	646.9	2250
Rb^+	788.9	687.9	612	625	2170
Cs^+	758.5	668.2	635	602	2090
Mg^2+		2326			3795
Ca^2+					3414
Sr^2+		2127			3217

Notice that for pairs of ions with the same charges, there is a gradual fall-off in the lattice energy as either the cation or anion size increases. For example, compare the values in the table above for LiF, LiCl LiBr, and LiI, where the size of the anion is increasing through the series. Likewise, compare the values for LiF, NaF, KF, RbF, and CsF, where the size of the cation is increasing through the series. By contrast, there is a dramatic increase in lattice energy with an increase in the charge of the cation or anion, or both. Using the value for LiCl as a reference point, compare the value listed forMgCl₂ (larger cation charge), and for Li₂O (larger anion charge). MgO (both cation and anion charges larger) shows an even more dramatic increase, compared to LiCl.

Q3

Explain the following trends in lattice energy.

1. \(KF < CaO < ScN \)
2. \(NaCl > RbBr > CsBr \)
3. \(MgO > MgCl_2\)

Lewis Dot Diagrams

The first model that attempted to describe molecular bonding in terms of sharing of electrons was developed by G. N. Lewis and Irving Langmuir in 1916. In this model a covalent bond is formed when one or more pairs of electrons are shared between two atoms in such a way that each achieves the equivalent of a noble gas configuration. The electrons are usually represented by dots (\(^{\bullet}\) or \(:\)), with shared pairs (bonds) represented by a line for each pair (\(\ce{-}\), \(\ce{=}\), \(\ce{#}\)). For H₂ each H atom brings an electron to the bond, so through sharing the two nuclei have two electrons, equivalent to the configuration of He.

\[\ce{H^{\bullet}} + \ce{H^{\bullet}} \rightarrow \ce{H:H} \Rightarrow \ce{H–H} \nonumber \]

Each H has a net of 2 electrons through sharing.

For F₂ each F atom brings 7 electrons to the molecule, for a total of 14. Through sharing each achieves an octet of electrons.

Each F has a net of 8 electrons through sharing.

Most elements, with the exception of hydrogen, achieve an octet through sharing. Hydrogen achieves a pair, like He. For example, in CCl₄ all atoms achieve an octet.

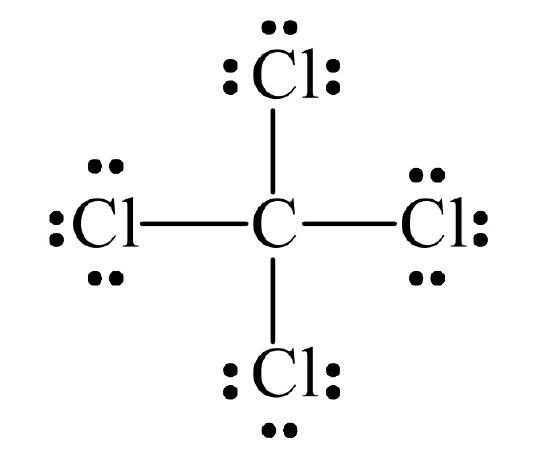
Each C–Cl bond is a single bond, defined as resulting from one electron pair shared between two atoms. The other electrons about each Cl are considered to be non-bonding electrons.

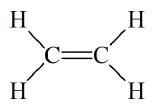
In some cases more than one bond can be formed between a pair of atoms. The carbon-carbon bond in C₂H₄ is a double bond in which two pairs of electrons are shared between the carbon atoms.

The carbon-oxygen bond in carbon monoxide is a triple bond, in which three pairs of electrons are shared between the carbon and oxygen atoms.

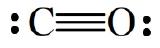
Bond order refers to the number of shared pairs forming bonds. Thus, the bond orders of a single, double, and triple bond are 1, 2, and 3, respectively. When two atoms can form bonds of varying bond order, the higher the bond order the stronger the bond will be. The measure of a bond’s strength is its dissociation energy, \(D\), which is the enthalpy required to break one mole of the bonds. Compare the following data for C-C bonds:

Compound	\(d_{C-C}\)	\(D_{C-C}\)
\(\ce{H3C–CH3}\)	1.54 Å	368 kJ/mol
\(\ce{H2C=CH2}\)	1.34 Å	435 kJ/mol
\(\ce{HC#CH}\)	1.20 Å	962 kJ/mol

Note that the bond lengths become shorter and the bond dissociation energies increase as bond order increases. In general, as bond order increases between a pair of atoms bond length decreases and bond strength increases.

The "octet rule" is sometimes violated with justifications. A few elements, particularly in groups 2 (Be) and 13 (B, Al) and some heavier elements in group 14 (Sn, Pb) occasionally form "electron deficient" compounds, in which the central atom has less than an octet. Examples of electron deficient compounds include BeH₂ in the gas phase and BF₃. On the other hand, some elements in the third and higher periods occasionally form compounds in which the central atom has more than an octet. This is called hypervalence. Examples of hypervalent compounds include PF₅, SF₆, and XeF₄. Only large central atoms from the third or higher periods are capable of forming hypervalent compounds, and only some of their compounds do so.

In order to construct Lewis models of bonding, you should follow the specific procedures detailed below, in the order given.

1. Arrange the atoms of the compound or complex ion so as to show how they are linked together by chemical bonds. When in doubt, assume that the least electronegative atom is central (not an outer atom). Hydrogen is almost always an outer (pendant) atom.
2. Count the valence electrons for each atom. For non-transition elements, the number of valence electrons is the same as the last digit of the group number (e.g., in group 16 there are 6 valence electrons). For a complex anion, add electrons equal to the negative charge. For a complex cation, subtract electrons equal to the positive charge. The total is the number of electrons to be used in generating the model.
3. ƒ Draw in single bonds (–) between all atoms that are linked together, keeping in mind that each bond represents the use of two electrons from the total established in step 2.
4. With the remaining electrons, first add pairs (:) to all of the outer atoms to make octets (except H), then add any leftover electrons to the central atom. The octet for each atom includes pairs used to make bonds in step 3.
5. Leave no electrons unpaired unless the total number of electrons is odd.
6. Count the number of electrons about the central atom to see if an octet has been made there. If not, try moving non-bonding pairs (:) from outer atoms to make double or triple bonds to the central atom. However, note that
   • hydrogen and the halogens do not form multiple bonds, and
   • elements in the third and higher periods usually do not form effective multiple bonds.
7. If there are too few electrons to give octets to all atoms (except hydrogen), the central atom might be electron deficient, particularly if it is Be, B, or Al. However,
   • outer atoms are never electron deficient, and
   • C, N, O, and F always have an octet, except in rare circumstances.
8. Sometimes central atoms from the third and higher periods have more than an octet (hypervalence), but only when necessary. However,
   • (a) outer atoms are never hypervalent, and
   • (b) C, N, O, and F are never hypervalent.
9. The representation of any anion or cation should be surrounded by square brackets ([ ]) with the charge indicated on the outside as a superscript.
10. Count up the number of electrons in the completed model to be sure it is the same as the total established in step 2.

Q4

Following the steps given above, draw Lewis dot structures for the following molecular species: NF₃, H₂O, NH₄⁺, SO₄^2–, H₂CO, C₂H₂.

Q5

Following the steps above, draw Lewis dot structures for the following molecular species, which may be electron deficient or hypervalent: AlCl₃, XeF₄, XeF₂, BeCl₂

Formal Charge

In terms of the "electron bookkeeping" of Lewis models, some bonds are formed by each atom contributing electrons. The bond in HCl fits this model.

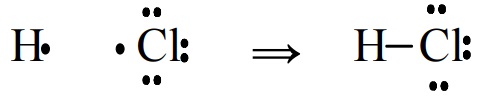
In other cases one atom seems to be donating a pair of electrons to the other. The P-O bond in Cl₃PO, formed from PCl₃ and an oxygen atom, illustrates.

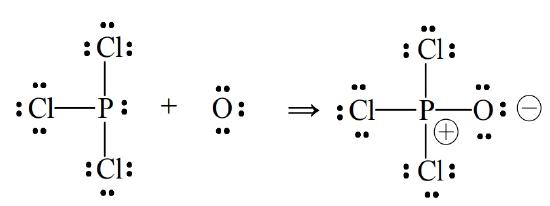
We might imagine that as a result of P–O bond formation the oxygen has gained electron density and the phosphorous has lost electron density. One way of indicating this kind of change in the electron environments about bonded atoms is through the use of formal charges of the type marked on the model of Cl₃PO. Formal charges can be described as the charges atoms would have if all elements had the same electronegativity. For example, if both H and Cl had equal attraction for the electrons in HCl there would be no net change in their electron environments. In Cl₃PO, by contrast, equal sharing of the pair between P and O would mean a loss of an electron by P and a gain of an electron by O, resulting in the formal charges indicated. Of course all electronegativities are not equal, so formal charges should only be regarded as a formalism, as the name suggests. They do not accurately reflect the actual distribution of charge across a molecule. Moreover, they do not represent real electronic charges (which is why they are written with a circle around them). Nonetheless, formal charge assignments, if used with care, can be qualitatively useful in deciding which of several possible Lewis dot models best represents the bonding in a molecule.

Formal charges are assigned to a Lewis dot model by a special set of bookkeeping rules for counting electrons:

1. Write the electron dot structure (Lewis dot model) for the compound or complex ion.
2. Count electrons about each atom by the following method (this is not the same as the method used to determine octets in constructing Lewis dot models.)
   • non-bonded pair (:) = 2
   • bonded pair (–) = 1
3. Compare the number of electrons counted in this manner with the number of valence electrons the isolated neutral atom would have.
4. If the count is higher than for the neutral atom, assign a negative formal charge equal to the difference. Write the formal charge inside a circle next to the atom (e.g., \(\ominus\)).
5. If the count is lower than for the neutral atom, assign a positive formal charge equal to the difference. Write the formal charge inside a circle next to the atom (e.g., \(\oplus\)).
6. The algebraic sum of all positive and negative formal charges for a neutral molecule should be zero. For a complex ion, it should equal the net charge on the ion.

Q6

Show the formal charges on all atoms in the sulfate ion, \(\ce{SO4^{2–}}\), whose Lewis dot structure you developed in Q4.

Resonance

Sometimes when we write the Lewis structure for a molecule we find that it is only one of two or more possible representations. Consider the Lewis structure for ozone, O₃. Either of the following two structures is equally likely.

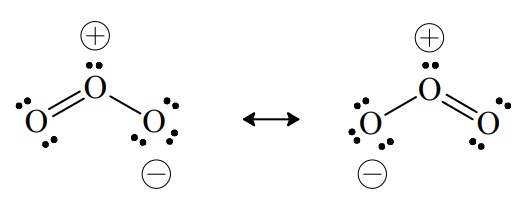
All experimental evidence suggests that both O–O bonds in ozone are equivalent and indistinguishable. This would not be the case if ozone consisted of one O–O single bond and one O=O double bond, as represented by either of the resonance forms above. The two equally likely resonance forms of ozone suggest that one of the two pairs used in forming a double bond in each structure really has equal probability over both bonds. In other words, a pair of electrons may be thought of as being delocalized over both bonds. This is in contrast to pairs that can be thought of as being localized in one bond between two atoms. If the true state of the molecule is an average of the resonance forms, then each O–O bond in ozone is really neither a true single bond, nor a true double bond. Rather, it must be something in between. If we associate one unit of bond order (B.O. = 1) with each shared pair, then the bond order for each O–O bond could be estimated to be 1½, the result of three pairs shared over two equivalent bonds. Comparison of bond length and dissociation energy data for O–O bonds in a variety of compounds is consistent with this conclusion.These two equivalent representations are called resonance forms or canonical forms. Neither by itself is an adequate representation of the bonding in ozone. Indeed, neither represents the state of the molecule in its lowest-energy state (its ground state). The true state of the molecule is an average of these hypothetical extreme structures. The need to postulate multiple resonance forms is actually only a manifestation of the limited ability of Lewis models to represent the bonding for certain molecules, using only one representation.

Molecule	O-O B.O.	Length (Å)	D (kJ/mol)
H2O2	1	1.49	138
O3	1½	1.28	300
O2	2	1.21	496

In general, for one of several equivalent bonds in a structure represented by a set of equally contributing resonance forms, the bond order can be estimated as the number of electron pairs shared among the equivalent bonds (\(x\)) divided by the number of bonds (\(y\)):

\[ B.O. = \dfrac{x\, \text{bond pairs}}{y\, \text{equivalentpairs}} \nonumber \]

For ozone, we have three pairs over two equivalent bonds; i.e.,

\[B.O. = \dfrac{3}{2} = 1½. \nonumber \]

Sometimes a molecule that can be represented by a single Lewis dot model shows properties that suggest contributions from other resonance forms. Carbon dioxide is such a case. The Lewis model for \(\ce{CO2}\) seems adequate:

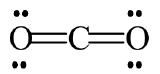
But a typical C=O double bond is expected to be 1.22 Å, whereas the measured distance in \(\ce{CO2}\) is 1.15 Å, a bit short. We can rationalize the shorter distance by assuming minor contributions from the following two canonical forms:

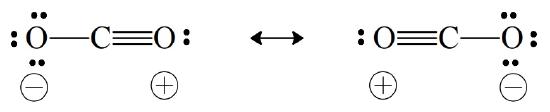
The formal charges, separated as they are across the molecule, suggest that these are less likely forms than the model that has no formal charge separation. Consequently, they are expected to be minor contributors to the description of the overall bonding in \(\ce{CO2}\). Nonetheless, their inclusion is consistent with the observed shorter bond length. In a case such as this, where all canonical forms do not contribute equally, we cannot give a numerical value for the bond order. Nonetheless, we can rationalize differences in bond strength and length.

Canonical forms are not real.

When discussing the bonding in a molecule that is a resonance hybrid, it is important to understand that the canonical forms are not real: no bond is flipping back and forth between being single, double, or triple. The goal in drawing resonance forms is to determine the collection of hypothetical extreme models whose average reasonably represents the electron distribution in the molecule. In keeping with this understanding, the following guidelines should be followed:

1. Draw all resonance structures (canonical forms) with exactly the same geometry, the same atom-pair linkages, and the same orientation on the page.
2. Do not move atoms from form to form. Only bonds to the same atoms change from form to form.
3. Where the "octet rule" is observed, all forms obey it.
4. The number of electron pairs must be the same across all forms.
5. Resonance forms that minimize formal charges, minimize formal charge separations, and avoid placing like formal charges on adjacent atoms are more reasonable and will be greater contributors to the overall description of the molecule.
6. Remember: Resonance forms are not real states of the molecule. The average of all the hypothetical resonance forms is suggestive of the actual electron distribution across the molecule.

Q7

The nitrate ion, \(\ce{NO_3^{–}}\), can be represented by a series of three equivalent resonance forms. Show the resonance forms of \(\ce{NO3^{–}\), including formal charges, and estimate the bond order of the N–O bonds in this ion.

Q8

\(\ce{FNO2}\) can be represented by three non-equivalent resonance forms. Draw the three canonical forms of FNO2 and assess their relative contributions to the resonance hybrid description of the molecule. What is the approximate N–O bond order?

Periodic Table of the Elements