10A: Periodic Trends (Worksheet)
- Page ID
- 81608
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Name: ______________________________
Section: _____________________________
Student ID#:__________________________
Work in groups on these problems. You should try to answer the questions without referring to your textbook. If you get stuck, try asking another group for help.
The size of an atom or ion and the attraction between the nucleus and the outermost electrons play important roles in determining the chemistry of an element. Knowing the trends in atomic and ionic sizes, ionization energies, and electron affinities aids in understanding chemical behavior and the nature of chemical bonds.
Learning Objective
- Know periodic trends of atomic size, ionic size, ionization energy, and electron affinity
- Understand the reasons for metallic, nonmetallic, and metalloid character
- Understand why some acids dissolve in water to make acidic solution, while others dissolve in water to make basic solutions
Success Criteria
- Be able to predict size differences among atoms and ions
- Be able to predict differences in ionization energy and electron affinity among elements.
- Be able to predict relative reactivity of related elements
- Be able to predict the acid-base character of oxides
Trends in Sizes of Atoms
Trends in sizes of atoms are the most important to understand, because other trends can often be rationalized on that basis. The most commonly used measure of size of an atom is its bonding atomic radius, also called the covalent radius (usually given in units of picometers (pm = 10–12 m) or Ångstroms (Å = 10–10 m) with 1 Å = 100 pm). The bonding atomic radius of an element is taken as one half the distance between the nuclei when two identical atoms are bonded together. For example, the internuclear distance in Cl2 is 198 pm, so the atomic radius is taken to be 99 pm or 0.99 Å. When two different atoms are bonded together their sizes can be altered. Nonetheless, the sum of their individual atomic radii is often used as a first approximation of the bond length between two different atoms. Thus, the length of a C–Cl bond in CCl4 is estimated to be the sum of the atomic radii of carbon (0.77 Å) and chlorine (0.99 Å), which is 1.76 Å. The experimentally determined distance is 1.766 Å.
The following plot shows how atomic radii vary through the periodic table.
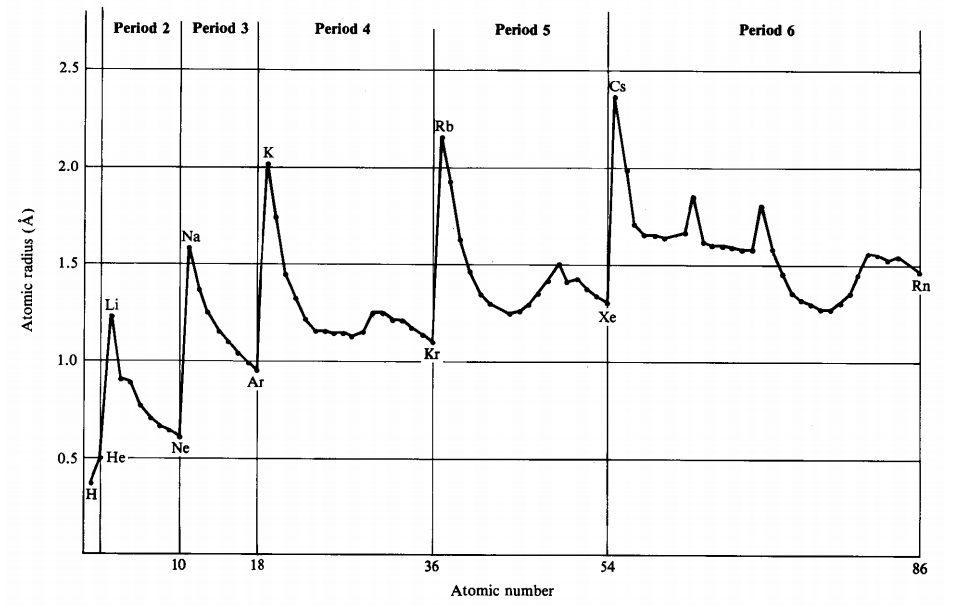
Across the periodic table, sizes of atoms show the following trends, with many irregularities:
- Size increases down a group. The outermost electrons are in successively more extensive orbitals as n increases.
- Size decreases across a period. Electrons are added to the same shell and do not shield one another very effectively from the increasing nuclear charge. This causes all orbitals (including the outermost size-determining orbitals) to contract as \(Z\) increases.
- Transition elements contract up to the middle of the series and then expand toward the end. Shielding becomes more effective after the d subshell is half filled. This makes the size-determining ns electrons move out further towards the end of each transition series.
- Lanthanides contract slowly across the series. This results from inefficient shielding by 4f electrons below the size-determining 6s electrons. The result is called the lanthanide contraction. Because the lanthanide filling occurs between the second and third transition series, the second and third transition elements in each period have nearly the same size. For example, both Ru and Os have a radius of 130 pm.
Q1
Using only a periodic table, predict the order of increasing atomic radius for each of the following sets of elements:
- Ca, Mg, Be
- Ga, Br, Ge
- Al, Tl, Si
- Zn, Cd, Fe
Q2
The experimentally determined Bi–Cl bond distance in bismuth trichloride is 2.48 Å. Given the tabulated value of 0.99 Å for the atomic radius of Cl, predict the atomic radius of Bi. If the experimentally determined Bi–I distance in bismuth triiodide is 2.81 Å, predict the atomic radius of I.
Sizes of Ions
Ionic radii for cations and anions are estimates, because it is virtually impossible to determine experimentally where the electron density of a cation begins and an anion ends in any ion pair. Tabulated values of ionic radii represent values that most consistently predict the measured separations between typical cation-anion pairs in many binary ionic compounds. The trends in ion sizes are very regular, with virtually no exceptions.
Ionic radii of ions increase with negative charge and decrease with positive charge.
Compare radii (in picometers, pm) for the following isoelectronic species (isoelectronic means “same number of electrons”) with the Ne configuration (ten electrons):
| O2– | F– | Na+ | Mg2+ | Al3+ |
| 140 | 133 | 97 | 66 | 51 |
Notice that for this series size increases with negative charge and decreases with positive charge. In the cases of the anions, there are more electrons than protons in the nucleus. This means that each electron is held about the nucleus with less than one equivalent positive charge, so the entire electron distribution expands. The reverse occurs with the cations. Here there are fewer electrons than protons, so each electron is held about the nucleus with more than one equivalent positive charge. Thus, the entire electron distribution is drawn closer to the nucleus.
The same trends can be seen in differently charged ions of the same element. For example, compare the radii for \(Cu(I)\) and \(Cu(II)\) ions:
\(\ce{Cu^{+}}\): 96 pm vs. \(\ce{Cu^{2+}}\): 69 pm
Ionic radii increase down a group for ions of the same charge.
In the chart below, note the trends in the sizes (radii in picometers, pm) of the following ions with the same charge.
| Li+ 60 | Be2+ 31 | O2– 140 | F– 136 | |
| Na+ 95 | Mg2+ 65 | Al3+ 50 | S2– 184 | Cl– 181 |
| K+ 133 | Ca2+ 99 | Ga3+ 62 | Se2– 198 | Br– 195 |
| Rb+ 148 | Sr2+ 113 | In3+ 81 | Te2– 221 | I– 216 |
| Cs+ 16 | Ba2+ 35 | Tl3+ 9 |
Q3
For each of the following sets of atoms and ions, arrange the members in order of increasing size.
- \(\ce{Se^{2–}, Te^{2–}, Se}\)
- \(\ce{Co^{3+}, Fe^{2+}, Fe^{3+}}\)
- \(\ce{Ca, Ti^{4+}, Sc^{3+} }\)
- \(\ce{S^{2–}, Se^{2–}, Ar}\)
Ionization Energy
Ionization energy, I, is the energy required to remove an electron from a gaseous species. The first ionization energy, \(I_1\), refers to removing one electron from a neutral atom:
\[X(g) \rightarrow X^+(g) + e^– \nonumber \]
with \(ΔE = I_1 > 0\)
All ionization energies are positive, because it takes energy to remove an electron from the attraction of an atom’s nucleus. Trends in first ionization energies can be understood on the basis of size of atoms. The valence electrons are closer to the nucleus to which they are attracted in a smaller atom; thus, more energy will be required to remove an electron by ionization. Consistent with size trends, first ionization energies generally increase across a period and decrease down a group. The following plot shows the variation of first ionization energies across the periodic table. The irregularities (“jogs” in the lines within a period) are the result of especially stable electronic configurations either in the neutral atom (resulting in a somewhat higher ionization energy) or the +1 ion produced by the ionization (resulting in a somewhat lower ionization energy).
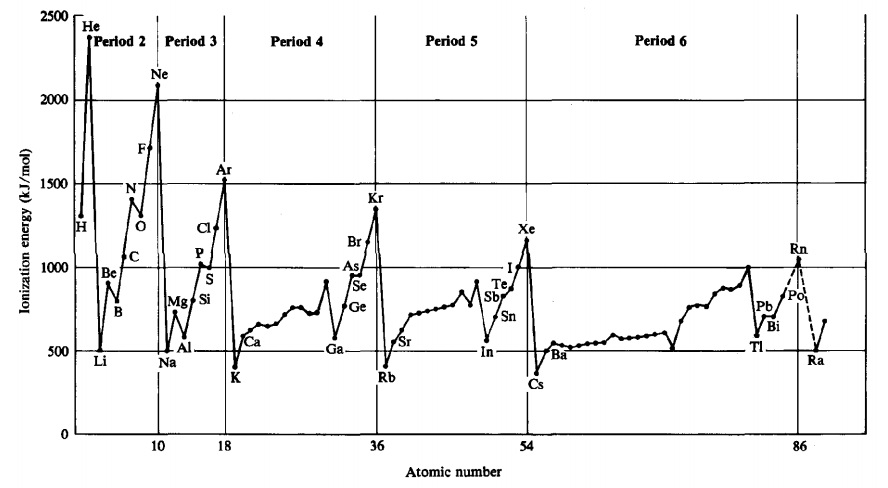
Second and succeeding ionization energies (I2, I3, ...), which remove additional electrons, require larger and larger amounts of energy, because each electron is being removed from a smaller species with an increasingly positive charge (a cation). For example, compare the first and second ionization energies of calcium:
| First Ionization | \(\ce{Ca(g) \rightarrow Ca+(g) + e–}\) | \(I_1 = 589.8\, kJ/mol\) |
| Second Ionization | \(\ce{Ca+(g) \rightarrow Ca2+(g) + e– }\) | \(I_2 = 1145.4\, kJ/mol\) |
| Total (sum) | \(\ce{Ca(g) \rightarrow Ca2+(g) + 2e– }\) | \(I_1 + I_2 = 1735.2\, kJ/mol\) |
Q4
Based on position in the periodic table, which element of the following pairs has the higher first ionization energy?
- O vs. Ne
- Ca vs. Sr
- K vs. Cr
- Br vs Sb
- In vs. Sn
Q5
First ionization energies tend to increase across a period. But in period 2, Be has a higher first ionization energy than B, and N has a higher first ionization energy than O. Explain, [Hint: Look at the valence configurations, and recall that half-filled and fully filled subshells have extra stability.]
Electron Affinity
Electron affinity is defined by the general reaction
\[A(g) + e^– \rightarrow A^–(g) \nonumber \]
with \(ΔH^o \equiv A\).
In general, the additional electron is added to a lowest-energy vacant orbital in the valence subshell, or in the next subshell if all valence subshells are already full. First electron affinities can be either exothermic or endothermic, depending on whether the atom "wants" the additional electron or not.
- \(A < 0\): the reaction is exothermic and the atom "wants" electron
- \(A > 0\): the reaction is endothermic and atom "doesn't want" electron
Although first electron affinities may be either positive or negative, all second and succeeding electron affinities are positive (endothermic). This is the result of repulsions between the additional electron and the negative ion that was formed in the first electron affinity process. For example, consider the stepwise formation of \(\ce{O^{2-}(g)}\):
| First Attachment | \(\ce{O(g) + e^{–} \rightarrow O^{–}(g)}\) | \(A_1 = -142 \,kJ/mol\) |
| Second Attachment | \(\ce{O-(g) + e^{–} \rightarrow O^{2–}(g)}\) | \(A_2 = +844\, kJ/mol\) |
| Total (sum) | \(\ce{O(g) + 2e^{–} \rightarrow O^{2–}(g) }\) | \(A_{tot} = +702\, kJ/mol\) |
Electron affinity data are limited, owing to experimental difficulties, and values vary greatly, depending on the source of the data. The following table of electron affinity data gives typical values (kJ/mol).
| 1A | 2A | 3A | 4A | 5A | 6A | 7A |
|---|---|---|---|---|---|---|
| H -73 | ||||||
| Li -60 | Be +100* | B -27 | C -122 | N +9* | O -141 | F -328 |
| Na -53 | Mg +30* | Al -44 | Si -134 | P -72 | S -200 | Cl -348 |
| K -48 | Ca ? | Ga -30 | Ge -120 | As -77 | Se -195 | Br -325 |
| Rb -47 | Sr ? | In -30 | Sn -121 | Sb -101 | Te -190 | I -295 |
| Cs -45 | Ba ? | Tl -30 | Pb -110 | Bi -110 | Po -183 | At -270 |
*Estimated value
In general, the gross trends in first electron affinities are:
- Electron affinities tend to become more negative across a period. This is the result of progressively smaller atomic sizes, placing the added electron closer to the nucleus.
- Electron affinities tend to become less negative (or positive) down a group . The added electron is placed in an orbital that is progressively further away from the nucleus.
- Nonmetals tend to have high (negative) electron affinities, and metals tend to have low (slightly negative or positive) electron affinities. This is consistent with the tendency of nonmetals to form anions, while metals resist forming negative ions.
- Noble gases have positive electron affinities. The added electron is placed in a higher-energy orbital above a very stable closed-shell configuration. The combination of high nuclear charge shielding and disruption of a stable configuration mitigates anion formation.
Q6
On the basis of electronic configurations or any other appropriate considerations, explain the differences in the electron affinities of the following pairs of species.
- Na, A1 < 0; Mg, A1 > 0
- N, A1 > 0; O, A1 < 0
- Br, A1 << 0; Kr, A1 > 0
- O, A1 < 0; O–, A2 > 0
Periodic Trends in Chemical Properties
The chemical behavior of elements is a consequence of their electronic structure. Not surprisingly, similarities in the behavior of elements in the same group are a result of their having the same kind of valence configuration. The differences are often a matter of degree, reflecting changes in the attraction between the nucleus and valence electrons (i.e., effective nuclear charge). For example, both \(\ce{Li}\) and \(\ce{Na}\) react with water to form aqueous solutions of their ionic hydroxides and hydrogen gas:
\[\ce{2 Li(s) + 2 H2O(l) \rightarrow 2 LiOH(aq) + H2(g)} \nonumber \]
\[\ce{2 Na(s) + 2 H2O(l) \rightarrow 2 NaOH(aq) + H2(g)} \nonumber \]
The reaction with lithium is very gentle, but with sodium it usually results in an explosion of burning hydrogen in air. The difference is understandable by comparing the smaller size and higher ionization energy of lithium with the larger size and lower ionization energy of sodium. In short, the energy input is less in the case of sodium, and the reaction’s exothermic energy output is greater.
As we have seen, elements can be categorized as metals, nonmetals, and metalloids. Each category has a characteristic range of ionization energies and electron affinities.
- Metals – low ionization energies, low electron affinities (negative or weakly positive)
- Nonmetals – high ionization energies, high electron affinities (negative)
- Metalloids - intermediate ionization energies and electron affinities
Owing to their relatively low ionization energies, metals tend to form cations, and when they combine with nonmetals they form ionic substances. For example, when metals combine with oxygen they form ionic oxides.
\[\ce{4 Fe(s) + 3 O2 \rightarrow 2 Fe2O3(s)} \nonumber \]
Metal oxides tend to dissolve in water to form hydroxide ion (\(\ce{OH^{–}}\)). Therefore, metal oxides are basic.
\[\ce{Na2O(s) + H2O(l) \rightarrow 2 NaOH(aq)} \nonumber \]
This is a result of the hydrolysis of the \(\ce{O^{2–}}\) ion in water:
\[\ce{O^{2–}(aq) + H2O(l) \rightarrow 2 OH^{–}(aq)} \nonumber \]
Nonmetals have ionization energies that are too high for stable cation formation, but their favorable electron affinities tend to result in anion formation. When combined with metal cations or complex cations, the resulting compounds are ionic. However, when nonmetals combine with each other, the compounds are molecular. In contrast to metals, the oxides of nonmetals are acidic. In molecular oxides, there are no oxide ions, and the oxygen is too tightly bound to be hydrolyzed into hydroxide ion in water. Instead, the nonmetal oxides tend to add both oxygen and hydrogen from water to make a molecular acid.
\[\ce{CO2(g) + H2O(l)} \rightarrow \underbrace{\ce{H2CO3(aq)}}_{\text{carbonic acid}} \nonumber \]
\[\ce{N2O5(s) + H2O(l)} \rightarrow \underbrace{ \ce{2 HNO3(aq)}}_{\text{nitric acid}} \nonumber \]
\[\ce{P4O10(s) + 6 H2O(l)} \rightarrow \underbrace{ \ce{4 H3PO4(aq)}}_{\text{phosphoric acid}} \nonumber \]
Properties of metalloids fall between metals and nonmetals. To behave as metals, metalloids such as \(\ce{Si}\), \(\ce{Ge}\), As would have to form very highly charged cations: (\(\ce{Si^{4+}}\), \(\ce{Ge^{4+}}\), \(\ce{As^{5+}}\)). Such small and highly charged cations would have a strongly attractive effect on the electrons around any anions with which they might combine. This would cause considerable sharing of electron density between the two. As we will see, sharing of electron density tends to be associated with molecule formation. Therefore, the oxides of metalloids are usually not ionic, and are generally not basic, as would be the case for true metals. They may have no acid-base character in water (essentially inert) or may be acidic (like molecular oxides).
\[\underbrace{ \ce{SiO2(s) + H2O(l) \rightarrow } \, \text{no reaction}}_{\text{inert behavior}} \nonumber \]
\[\underbrace{ \ce{As2O5(s) + 3 H2O(l) \rightarrow 2 H3AsO4(aq)}}_{\text{acid oxide behavior}} \nonumber \]
Q7
Calcium is generally less reactive than potassium but more reactive than magnesium. Explain.
Q8
For each of the following oxides, indicate whether it is ionic or molecular and whether it is acidic or basic. Then, write a balanced equation for the reaction expected between each oxide and water: \(\ce{SO2(g)}\), \(\ce{CaO(s)}\), \(\ce{Li2O(s)}\), \(\ce{SeO3(s)}\), and \(\ce{P4O6(s)}\).
Periodic Table of the Elements