9A: Quantum Mechanical Model of Electronic Structure (Worksheet)
- Page ID
- 81599
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\(\newcommand{\ket}[1]{\left| #1 \right>} \)
\( \newcommand{\bra}[1]{\left< #1 \right|} \)
\( \newcommand{\braket}[2]{\left< #1 \vphantom{#2} \right| \left. #2 \vphantom{#1} \right>} \)
\( \newcommand{\qmvec}[1]{\mathbf{\vec{#1}}} \)
\( \newcommand{\op}[1]{\hat{\mathbf{#1}}}\)
\( \newcommand{\expect}[1]{\langle #1 \rangle}\)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Name: ______________________________
Section: _____________________________
Student ID#:__________________________
Work in groups on these problems. You should try to answer the questions without referring to your textbook. If you get stuck, try asking another group for help.
- Understand quantum numbers and their restrictions
- Understand the relationship between quantum numbers and orbitals
- Understand the description of electron behavior on the basis of orbitals
- Understand the extension of the one-electron wave mechanical model to multielectron atoms
- Understand the relationships between configurations of neutral atoms and those of their ions
Success Criteria
- Be able to determine allowable combinations of quantum numbers
- Be able to sketch the basic types of atomic orbitals and know what they represent
- Be able to apply the aufbau principle to write electronic configurations of multielectron atoms
- Be able to distinguish and write complete configurations, core notation configurations, and valence configurations of atoms and ions.
- Be able to write electronic configurations in shell order, rather than aufbau order
Bohr’s model of the atom, which was so successful in explaining the line spectra of single-electron atoms, was a total failure in all attempts to describe multielectron atoms. By the 1930s it was supplanted by an approach that recognized the wave-particle dual nature of subatomic particles, the Schrödinger wave equation model. This is the basis of the model all chemists use today. Not only does it describe the electronic structure of atoms, it also is the foundation of our models of molecular structure and bonding in molecules.
Wave Equation & Quantum Numbers
In 1926, Erwin Schrödinger extended de Broglie's ideas of the wave nature of matter to describe the wave behavior of particles that are not freely moving, but rather are constrained to a certain region, such as electrons about a nucleus in an atom. Schrödinger's wave mechanics, as it became known, was first applied to the one-electron atomic cases, as Bohr's model had been. But unlike Bohr's model, quantization was a result of the approach, rather than an add-on assumption. Furthermore, the Schrödinger model was consistent with the new physics of wave-particle duality and the uncertainty principle, articulated by Heisenberg.
The Schrödinger wave mechanical approach expresses the energy of an electron in an atom in terms of a mathematical expression that uses both wave and particle quantities, in keeping with the idea of wave-particle duality. The mathematical expression on which this description is based is called the wave equation. It has the following general form
\[HΨ = EΨ \label{SE} \]
The symbol \(H\) represents a Hamiltonian operator, which mathematically operates on \(Ψ\), the wavefunction. There are many solutions to this equation, each of which is a mathematical expression for Ψ. The various wave function solutions describe the behavior of the electron when it has a certain associated energy, E. Much to his consternation, Schrödinger realized that the wave functions have no physical meaning. However, using an analogy to optics, the allowed Ψs can be related to something that is physically meaningful. For light the intensity is proportional to the square of the amplitude of the wave; i.e., \(I \propto A^2\). If we think of \(Ψ\) as an "electron wave", then \(Ψ^2\) could be seen as the "intensity" of the electron. If we calculate this "intensity" for any small volume in space (virtually a point) it can be taken as a measure of the probability of finding the electron at that point; i.e.,
\[P \propto Ψ^2 \nonumber \]
So, today we think of the wave mechanical model of the atom in terms of varying probabilities of finding the electron about the vicinity of the nucleus.
\(Ψ\) cannot be factored out of Equation \ref{SE}, because the Hamiltonian operator operates on \(Ψ\) in the same sense that a square root sign or integral sign operates on the mathematical symbols that follow. Moreover, the Hamiltonian operator contains information about the potential and kinetic energy of the atomic system. The explicit Schrödinger equation for any system containing electrons is an expression involving advanced calculus (differential equations). The only case that has been set up and solved exactly is the one-electron system, such as \(\ce{H}\), \(\ce{He^{+}}\), and \(\ce{Li^{2+}}\), etc..
The individual wave function solutions to the one-electron wave equation are defined by three quantum numbers, designated n, l, and ml. Each quantum number is associated with a particular aspect of the electron's behavior and the distribution of its probability in space around the nucleus of the atom.
Principal quantum number: \(n\)
Determines energy of the one-electron atom by the equation,
\[E =\dfrac{2 \pi^2 m X^2 e^4}{n^2h^2} = \dfrac{-BZ^2}{n^2} \nonumber \]
the allowed values are \(n = 1, 2, 3, \ldots\). The principal quantum number is related to the concept of shells.
Angular momentum (azimuthal) quantum number: \(l\)
This determines the shape of the probability distribution. Allowed values are
\[l = 0, 1, 2, ..., n - 1 \nonumber \]
The angular momentum quantum number is related to the concept of subshells. The subshells are designated by letter labels that correspond to the value of l:
| Value of l | 0 | 1 | 2 | 3 | 4 | ... |
|---|---|---|---|---|---|---|
| Label | s | p | d | f | g | ... |
After l = 3 the labels proceed alphabetically (omitting j), but subshells with such high values of l are not important for most chemistry.
Magnetic quantum number: \(m_l\).
This determines orientation of the probability distribution in three-dimensional space. Allowed values are
\[m_l = -l, (-l + 1), \ldots , 0, \ldots, (l - 1), +l \nonumber \]
The magnetic quantum number is related to concept of orbitals.
The wave functions associated with a given set of n, l, and ml values are used to define orbitals. Orbitals that have the same value of n are said to be in the same shell. Orbitals in the same shell that also have the same value of l are said to be in the same subshell. The shell and subshell are designated with a spectroscopic notation that indicates the value of n and the letter label for the value of l. The relationships among the values of the three quantum numbers n, l, and ml, the subshell spectroscopic notation, and the numbers of subshells and orbitals in a shell is shown below for the first four shells.
| n | l | Subshell Notation | Allowed ml values | Orbitals in Subshell |
|---|---|---|---|---|
| 1 | 0 | 1s | 0 | 1 |
| 2 | 0 | 2s | 0 | 1 |
| 1 | 2p | -1, 0, +1 | 3 | |
| 3 | 0 | 3s | 0 | 1 |
| 1 | 3p | -1, 0, +1 | 3 | |
| 2 | 3d | -2, -1, 0, +1, +2 | 5 | |
| 4 | 0 | 4s | 0 | 1 |
| 1 | 4p | -1, 0, +1 | 3 | |
| 2 | 4d | -2, -1, 0, +1, +2 | 5 | |
| 3 | 4f | -3, -2, -1, 0, +1, +2, +3 | 7 |
For the one-electron atom, the electron's energy depends solely on the value of n. This means that in any shell, all orbitals have the same energy. This result is the same as the Bohr result, because in both models the energy equation for one-electron atoms is the same. Recall that the Bohr equation correctly predicted the energies and emission spectra for all one-electron atoms. Therefore, if the wave equation approach has validity, it too should give the same energy equation. The important difference, however, is that the Schrödinger approach can be extended to multielectron atoms, using the same fundamental considerations as the one-electron case. The Schrödinger equation for any multielectron case is much more complicated and in general cannot be solved exactly. However, it is possible to construct approximate solutions. In any multielectron atom, the energy of each electron no longer depends solely on the value of n, but rather varies in a complicated way, depending on both n and l. Nonetheless, in both one-electron and multielectron atoms, all orbitals in the same subshell have the same energy. Orbitals that have the same energy are said to be degenerate.
Q1
The wave functions, which describe orbitals, are cast in terms of three quantum numbers. Fill in the table below with the name and allowed values for each quantum number.
| Number | Name | Allowed values |
|---|---|---|
| n | ||
| l | ||
| ml |
Q2
The table below shows various combinations of the three quantum numbers. Indicate which combinations are allowed and which are disallowed. For those that are allowed, give the subshell notation (e.g., 2p).
| n | l | ml | Allowed? | Notation |
|---|---|---|---|---|
| 3 | 2 | –1 | ||
| 4 | 0 | 0 | ||
| 2 | 2 | 1 | ||
| 5 | 1 | 1 | ||
| 4 | 3 | –2 | ||
| 4 | –3 | 0 |
Orbital Shapes
Although an atomic orbital is only a mathematical function describing the behavior of a single electron, chemists often think of orbitals as the region in space in which an electron can be found. This is often represented by a picture of a three-dimensional boundary surface, meant to represent the space inside which the electron is found with 90% probability. The following pictures show these kinds of representations for the possible orbitals with principal quantum number values \(n = 1, 2, 3\).
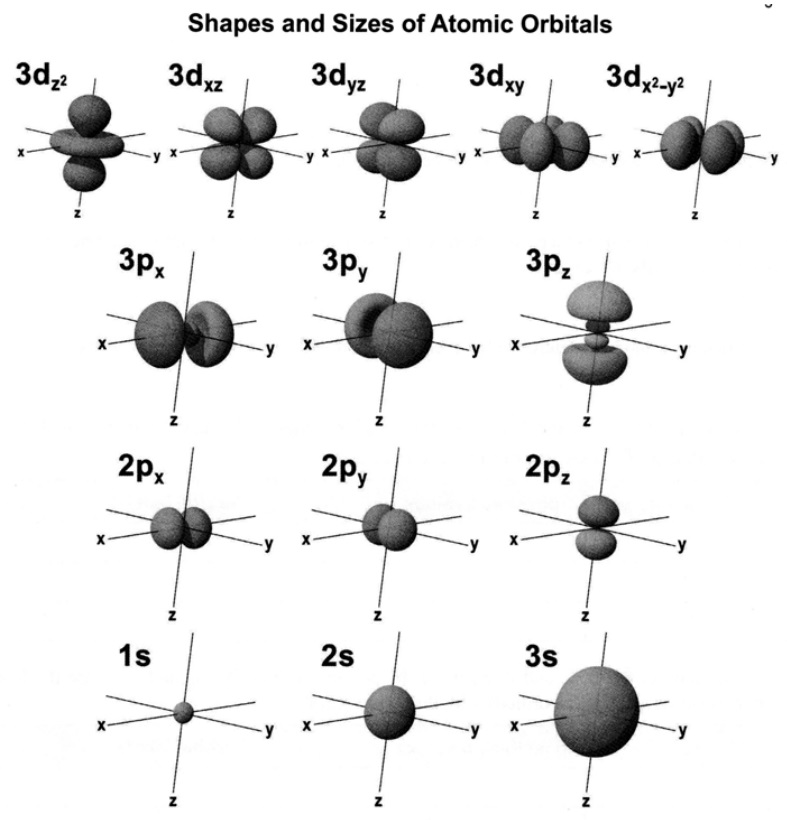
Many of the orbitals have regions in which the electron has no probability of being found (\(Ψ^2 = 0\)), called nodes. In s orbitals, which have a spherical distribution, the nodes are likewise spheres (i.e., radial nodes), as shown below.
.jpg?revision=1&size=bestfit&width=428&height=243)
Among s orbitals, 1s has no nodes, 2s has one node, 3s has two nodes, and so on. The \(p\) orbitals have nodal planes separating the two lobes. As n increases the higher np orbitals still have a single nodal plane, but they successively add spherical nodes that separate additional pairs of lobes along the same axis (e.g., compare sketches of 2pz and 3pz, above). The cloverleaf-type d orbitals have perpendicular nodal planes, which separate adjacent lobes and intersect at the nucleus. The dz2 orbital, has two nodal cones, which surround the two lobes and separate them from the doughnut around the middle. As \(n\) increases, nd orbitals add spherical nodes and additional lobes.
Although the shapes of orbitals of the same l value become more extensive, have more lobes, and have more nodes as n increases, in routine sketches of orbitals it is common practice to represent an orbital as the simplest example of its type. Thus, if we need to sketch a 3p orbital for a routine drawing, for simplicity we often show a sketch that is actually the shape of a 2p orbital, the simplest example of a p-type orbital. For routine hand drawings, the following sketches of “balloon models” are generally used.
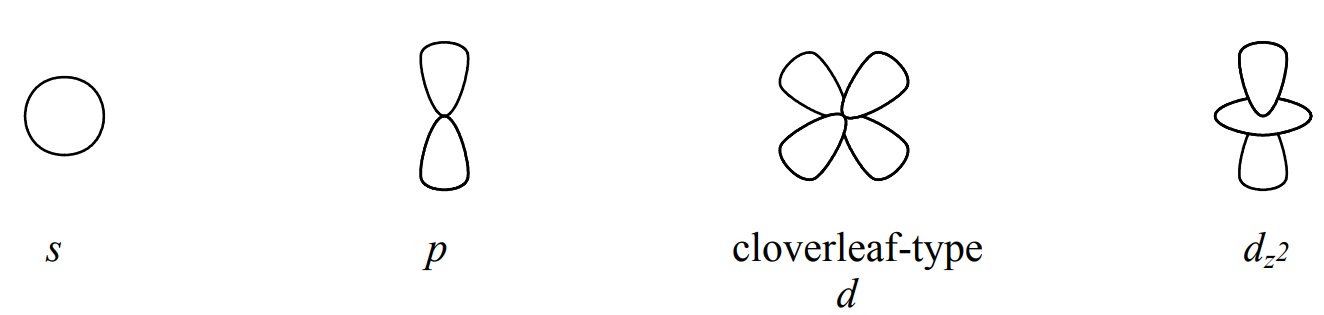.jpg?revision=1&size=bestfit&width=748&height=178)
We can summarize the features of orbitals for the one-electron atom with the following points:
- All orbitals with the same value of the principal quantum number n have the same energy; e.g., 4s = 4p = 4d = 4f. (This is not true for multielectron atoms.)
- The number of equivalent (degenerate) orbitals in each subshell is equal to 2l + 1.
- For orbitals with the same l value, size and energy increase with n; e.g., 1s < 2s < 3s.
- For orbitals of the same l value, the number of nodes increases with n.
| Orbital | 1s | 2s | 3s | 4s |
| Nodes | 0 | 1 | 2 | 3 |
| Orbital | 2p | 3p | 4p | |
| Nodes | 1 | 2 | 3 |
Q3
Describe the characteristic shapes of s, p, and d orbitals that distinguish them from each other?
Q4
Which quantum number identifies the shape of an orbital?
Q5
What happens to the size and number of nodes of a particular type of orbital (e.g., ns orbitals) as the principal quantum number increases.
Q6
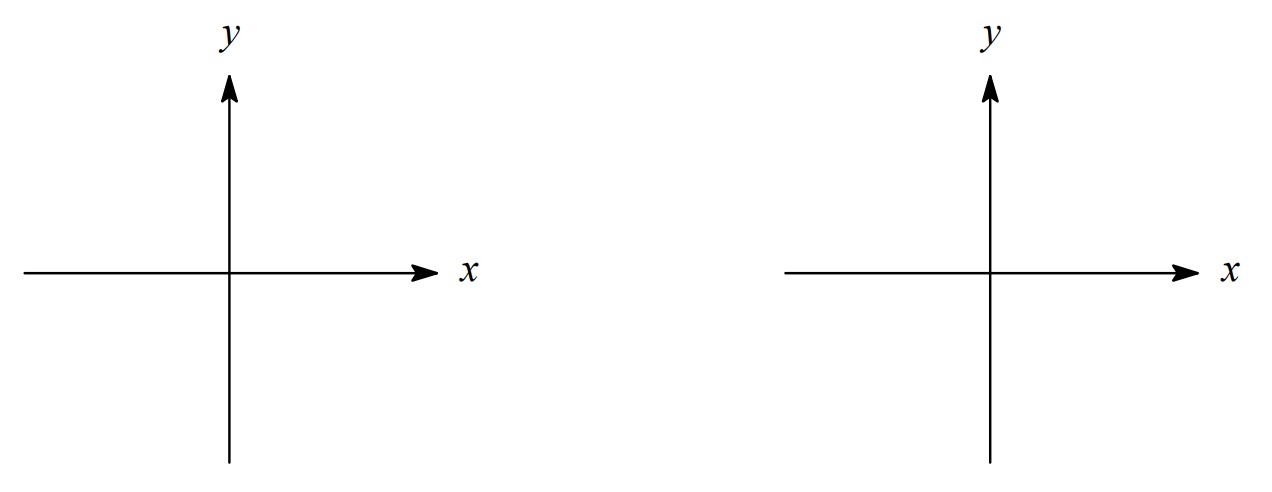
On the axes below, sketch a 3dxy orbital on the left and a 3dx2–y2 orbital on the right.
Electron Spin and Subshell Energies
An electron in an atom may have one of two possible magnetic orientations relative to an applied magnetic field, indicated by the spin quantum number, ms = ±½. By the Pauli Exclusion Principle, no two electrons in the same atom can have the same complete set of quantum numbers, n, l, ml, and ms. Thus, if two electrons have the same n, l, and ml values (i.e., are described by the same orbital), one must have ms = +½, and the other must have ms = –½. The two electrons are said to be paired in the same orbital.
Q7
In light of the Pauli Exclusion Principle, indicate the electron capacities of the following subshells:
3s 2p 5f 3d
Q8
In a one-electron atom the energy depends solely on n (e.g., 3s = 3p = 3d). In multielectron atoms, the energy depends on both n and l. List the following orbitals in order of increasing energy (i.e., most stable first): 4f, 3s, 4p, 2p, 3d.
Multielectron Atoms and Aufbau Process
The ground-state (lowest energy) configuration of an atom can be predicted by the aufbau procedure, a bookkeeping system in which electrons are filled sequentially into available orbitals by increasing energy, consistent with the Pauli Exclusion Principle. The energies of the various subshells vary in a complicated way with increasing nuclear charge, but the ordering of subshells at the point in which electrons are added in the aufbau process follows the pattern of the chart bellow, on which the order is indicate by following the arrows from right to left and top to bottom.
.jpg?revision=1&size=bestfit&width=336&height=530)
The complete electronic configuration is written in spectroscopic notation by showing the numbers of electrons in each subshell, written as a right superscript. For example, nitrogen (Z = 7) has the configuration 1s22s22p3.
Q9
Write the complete electronic configuration for each of the following atoms in their ground states.
- \(\ce{C}\)
- \(\ce{Cl}\)
- \(\ce{V}\)
- \(\ce{Ca}\)
- \(\ce{I}\)
- \(\ce{Tl}\)
Exceptional Configurations
Some transition metals, lanthanides, and actinides have irregular configurations. In some cases these can be understood on the basis of the extra stability afforded a half-filled or fully filled d or f subshell. You do not need to worry about all of these exceptions, but you should know the configurations of chromium and copper. Chromium and copper have half-filled and fully filled 3d subshells, respectively. Thus the outermost subshells of 24Cr have the filling 3d 54s1, rather than the expected configuration 3d 44s2. Likewise, the outermost subshells of 29Cu have the filling 3d 104s1, rather than the expected configuration 3d 94s2. In these cases, a lower energy results by having symmetrical distributions in the 3d subshell from either a half-filled or fully-filled configuration, rather than the unsymmetrical distributions represented by four or nine electrons.
Q10
Write the complete electronic configurations for \(\ce{Cr}\) and \(\ce{Cu}\).
Valence Configurations
When atoms form ionic and molecular compounds, it is the outermost electrons that are responsible for the chemical reactivity and bond formation. The configuration of these electrons is called the valence configuration. Inasmuch as these electrons are most responsible for the chemistry of the atoms, we are often only concerned with an atom's valence configuration, and not the configuration of lower lying electrons, which may be regarded as core electrons. Elements in the same group have the same valence configuration pattern, which is the reason behind their similar chemistries. In fact, we can partition the periodic table into various blocks according to the valence configuration pattern for elements in each region. For example, elements in the so-called s block, which fall in groups 1 and 2, have valence configurations that are either ns1 (group 1) or ns2 (group 2), where n is the period number of the element. The following table shows the patterns for all of the blocks.
| Block | Type | Valence Configuration |
|---|---|---|
| s | Groups 1 & 2 | nsx (x = 1, 2) |
| p | Nonmetals (Groups 13 - 18) | ns2npx (x = 1 - 6) |
| d | Transition metals | (n-1)d xnsy (x = 1 - 10; y = 0 - 2) |
| f | Lanthanides/Actinides | (n-2)f xnsy (x = 1 - 14; y = 0 - 2) |
In all of these, the value of n is the period in which the element can be found, and x is usually the period position within the block, counting from the left. (Exceptions for the value of x are frequent among transition elements, lanthanides, and actinides.) Knowing these patterns, you should be able to point to any element in the periodic table and write down its aufbau-predicted valence configuration. For example, 34Se (Z = 34) is a p-block element in the fourth period, and it is the fourth element from the left border of the p-block in that period. Thus, its valence configuration is 4s24p4.
Note that for d and f block elements, it is preferable to write the valence configuration in shell order; i.e., order of increasing principle quantum number (n). This logically places the first electrons lost in cation formation at the end. For example, 25Mn is better written 3d54s2, rather than in the aufbau order 4s23d5, because in forming Mn2+ it is the two 4s electrons that are lost, not any of the 3d electrons.
Q11
Looking at a periodic table, write down the valence configuration for each of the following elements: \(\ce{As}\), \(\ce{Ni}\), \(\ce{Cs}\), \(\ce{Cd}\), and \(\ce{Sr}\). (Practice this on your own so that you can do this without hesitation.)
Configurations in Shell Order
There are two ways of writing either a valence or complete electronic configuration: aufbau order or shell order. Aufbau order arranges the individual subshells in the order in which they are filled when following the aufbau process. Shell order is the same configuration, but written so that all the subshells are grouped by increasing n quantum number (grouped in shells), and within each shell by increasing l quantum number (s < p < d < f ). The valence configuration patterns in the table above are written in shell order. To see the difference, compare the two ways of writing the complete configuration of 84Po, whose valence configuration is 6s26p4. The valence electrons in each case are indicated in bold.
- Aufbau order: 1s22s22p63s23p64s23d104p65s24d105p66s24f145d106p4
- Shell order: 1s22s22p63s23p63d104s24p64d104f145s25p65d106s26p4
Note that in aufbau order the two subshells of the valence configuration are separated by 4f145d10, which is part of the core configuration. But in shell order all the valence electrons are grouped together at the end. This will always be the case, and that is the principal advantage of writing configurations this way. In shell order, you will be less likely to make mistakes when forming cations or anions (taking away or adding electrons, respectively), because it makes sense to do these alterations on the last-listed subshells.
If you can write down the valence configuration from the element’s position, you can use the periodic table as a kind of road map to write down the complete electronic configuration quickly. With the valence configuration in hand, the question is “What subshells had to be filled to get from hydrogen to here?” To illustrate this, consider again 84Po, whose valence configuration is 6s26p4. To get to Z = 84, we follow the path in the periodic table from hydrogen to polonium. (Follow this on a periodic table.) Clearly, in passing through the first two periods we had to fill the first two shells; i.e., 1s22s22p6. We then passed through the third period and the first transition series in the fourth period, where 3d is filled, so we must have filled all the possible subshells for n = 3; i.e., 3s23p63d10. After that, we passed through the second transition series, where 4d is filled, but we also had to pass through the lanthanides, where 4f is filled. Therefore, all the possible subshells for n = 4 are filled; i.e., 4s24p64d104f14. We passed through the third transition series, where 5d is filled, but we did not pass through the actinides. Therefore, for n = 5 we will fill all the subshells except 5f; i.e., 5s25p65d10. The remainder is the valence configuration 6s26p4. Putting it all together gives the shell order configuration shown above. Doing it this way, you will discover that you can write down the complete configuration in shell order more quickly and more accurately than you could by slavishly following the aufbau order of writing. And, the valence configuration will be at the end, where it belongs!
Q12
Consider gold, 79Au, whose valence configuration is irregular in the same way as Cu and Ag.
- Write the valence configuration of Au in shell order.
- Write the complete electronic configuration of Au in shell order.
- Write the valence configuration of Au+ by removing one electron from the highest energy occupied subshell in the configuration of neutral Au.
- Write the valence configuration of Au3+ by removing two electrons from the highest energy occupied subshell in the configuration of Au+.
Noble-gas Core Notation
Rather than writing out the complete electronic configuration, we often use a shorthand form, sometimes called condensed or noble-gas core notation. In this form, the electronic configuration of the nearest noble-gas element of lower atomic number is represented by its symbol in brackets, and then the remaining configuration is written after this. This is often just the valance configuration, but for elements following a transition series or lanthanide series this includes filled d or f subshells, which are not valence electrons. In this notation, \(\ce{Se}\) is written as [Ar]3d104s24p4. Here, 3d 10 is part of the core configuration (not the valence configuration); the valence configuration is just 4s24p4.
Q13
Write the condensed electronic configurations for the elements whose valence configurations you wrote in Q11.
Configurations of Ions
When atoms form ions, electrons are added to the lowest energy subshell with vacant orbitals (anion formation) or are taken from the highest occupied subshell (cation formation). For cations of transition elements, this always means taking the ns electrons before taking any (n–1)d electrons. Thus, in condensed notation the configuration for \(\ce{Co^{2+}}\) is [Ar]3d 7, not [Ar]3d 54s2.
Q14
Write the condensed electronic configurations for the following ions: \(\ce{Se^{2–}}\), \(\ce{Sr^{2+}}\), \(\ce{Cd^{2+}}\), \(\ce{Fe^{2+}}\), \(\ce{Fe^{3+}}\), and \(\ce{Tl^{+}}\).
Box-and-Arrow Diagrams
By Hund’s Rule of Maximum Multiplicity, when applying the aufbau procedure to determine the ground-state configuration, electrons are added to a subshell with parallel spins (i.e., not paired) so long as the Pauli Exclusion Principle allows. Electron pairing begins only after a subshell is half filled. We can visualize the paired and unpaired electrons in the valence configuration by an orbital diagram, sometimes called a line-and-arrow diagram or a box-and-arrow diagram. As an example, the valence configuration of 8O is represented by the following box-and-arrow diagram:
.jpg?revision=1&size=bestfit&width=344&height=113)
Q15
Draw box-and-arrow diagrams for the valence configurations of \(\ce{Fe}\), \(\ce{Fe^{2+}}\), and \(\ce{Fe^{3+}}\).
Periodic Table of the Elements