8A: Thermochemistry (Continued), Electromagnetic Radiation, and Line Spectra (Worksheet)

Name: ______________________________

Section: _____________________________

Student ID#:__________________________

Work in groups on these problems. You should try to answer the questions without referring to your textbook. If you get stuck, try asking another group for help.

As we saw last week, enthalpy and internal energy are state functions, which means that the sum of the heats of any set of steps that adds to give an overall reaction will have the same heat as doing the reaction directly. This is Hess’s Law. We will revisit this today and go on to see that if we use a special kind of thermochemical reaction, called the standard enthalpy of formation, we can calculate enthalpies of reactions without having to manipulate a series of individual thermochemical equations for each step.

To understand the modern model of atomic structure, we need to look at the nature of light and other forms of electromagnetic radiation. One of the most important ideas to emerge at the start of the twentieth century was that energy of subatomic particles and electromagnetic radiation is not continuous, but rather is quantized in discrete allowable values. An understanding of the basic relationships among the characteristic properties of electromagnetic radiation and an appreciation of the nature of state-to-state transitions in quantized systems will lay a foundation for understanding the modern quantum mechanical model of the atom.

Learning Objectives

• Understand Hess’s Law
• Understand the definition and use of standard enthalpy of formation
• Understand the fundamental relationships of electromagnetic radiation and the electromagnetic spectrum
• Understand the relationship between line spectra and the quantum concept

Success Criteria

• Be able to calculate enthalpy of a target reaction from a series of given reactions
• Be able to apply standard enthalpies of formation to calculate the enthalpy of a reaction
• Be able to do conversions between energy, wavelength, and frequency of electromagnetic radiation
• Be able to correlate state-to-state transitions with region of the electromagnetic spectrum and calculate the energy of a state-to-state transition

Standard Conditions, State Functions and Hess's Law

Remember that the measured value of ΔH depends on the states of all reactants and products (s, l, g, aq) and the temperature and pressure under which the reaction occurs. In order to make meaningful direct comparisons, it is useful to define a set of standard conditions. By international agreement, standard conditions are defined as T = 25 ^oC; P = 1 atm; all substances in their usual states for these conditions (the standard state). The standard state of an element is its most stable state; e.g., H₂(g), C(s) – graphite, S₈(s), P₄(s). For compounds, the standard state is the most prevalent state under standard conditions; e.g., H₂O(l), CO₂(g), C₂H₂(g), C₆H₆(l).

Enthalpy is a state function, which only depends upon current conditions (the state of the system) for its value, not on how the current state was reached. As applied to ΔH = H_f – H_i, the value of the enthalpy change for any process depends only on the difference between the final and initial states, not on the path chosen. This means that any set of steps, whether real or imagined, that take the system from the initial state to the final state of interest will have a sum of ΔH values for all the steps that is equal to the value of ΔH for the overall process done directly. This principle, called Hess's Law of Constant Heat Summation, was first established by G. H. Hess in 1840:

The enthalpy change for a reaction is independent of path.

In applying Hess's Law, a set of given thermochemical equations is manipulated such that they add to give a balanced thermochemical equation for the process of interest (the target equation). In doing this, whenever a given thermochemical equation is multiplied (usually by an integer or rational fraction), its \(ΔH\) is likewise multiplied. Whenever the direction of a given thermochemical equation is reversed, its \(ΔH\) value changes sign.

Q1

Calculate \(ΔH^o\) for this hydrogenation reaction,

\[\ce{C2H2(g) + H_2(g) \rightarrow C2H4(g)} \nonumber \]

Given:

\[\ce{2 C2H2(g) + 5 O2(g) \rightarrow 4 CO2(g) + 2 H2O(l)} \nonumber \]

with \(ΔH^o = –2599.2\, kJ\) and

\[\ce{ C2H4(g) + 3 O2(g) \rightarrow 2 CO2(g) + 2 H2O(l)} \nonumber \]

with \(ΔH^o = –1410.9\, kJ\) and

\[\ce{H2(g) + 1/2 O2(g) \rightarrow H2O(l)} \nonumber \]

with \(ΔH^o = –285.8\, kJ\).

Standard Enthalpies of Formation: \(ΔH^o_f\)

Hess’s Law calculations are done so frequently that it is convenient to have tabulated data for a large number of reactions. The most generally useful data for these kinds of calculations are standard enthalpies of formation.

The standard enthalpy of formation, ΔH^o_f, of a compound is the enthalpy change for the reaction in which one mole of the compound in its standard state is made from the stoichiometric amounts of its elements in their standard states. For all elements in their standard states, ΔH^o_f = 0, by definition.

For example, the following thermochemical equations define standard enthalpies of formation for \(\ce{C2H2(g)}\) and \(\ce{C2H4(g)}\), respectively.

\[\ce{2 C(s) + H2(g) \rightarrow C2H2(g)} \label{a} \]

with \(ΔH^o_f = +226.8 \,kJ\) and

\[\ce{2 C(s) + 2 H2(g) \rightarrow C2H4(g)} \label{b} \]

with \(ΔH^o_f = +52.3 \,kJ\).

Notice that each of these equations gives the heat produced when exactly one mole of the product compound is made. There are no thermochemical equations for the formation of substances such as \(\ce{C(s)}\) as graphite or \(\ce{H2(g)}\) as the gaseous element, because these are their normal elemental states. Their standard enthalpies of formation are set as zero by definition.

Let’s use the two enthalpy of formation equations given above to calculate the enthalpy of the following reaction:

\[\ce{C2H2(g) + H2(g) \rightarrow C2H4(g)} \nonumber \]

with \(ΔH^o = ?\).

You calculated the enthalpy of this reaction in Q1, but now we are going to do it with the thermochemical equations that define \(ΔH^o_f\) for \(\ce{C2H2(g)}\) and \(\ce{C2H4(g)}\). To do this, we simply need to take the reverse of Equation \ref{a} with the negative of its given enthaply, and add it to Equation \ref{b}, using its given enthalpy. The resulting sum is:

Action	Reaction	\(ΔH^o_f\)
- Equation \ref{a}	\(\ce{C2H2(g) \rightarrow \cancel{2 C(s)} + \cancel{H2(g)}}\)	–226.8 kJ
Equation \ref{b}	\(\ce{ \cancel{2 C(s)} + \cancel{2} H2(g) \rightarrow C2H4(g)}\)	+52.3 kJ
sum (and cancel)	\(\ce{C2H2(g) + H2(g) \rightarrow C2H4(g)}\)	–174.5 kJ

This is the same answer you obtained in Q1, as expected on the basis of Hess’s Law. But notice that the answer we obtain here is the following sum, where ΔH^o_f (H₂) = 0, because H₂(g) is an element in its standard state:

\[ \begin{align} ΔH^o_{rxn} &= ΔH^o_f(\ce{C2H4}) - \left[{\Delta H^o_f(\ce{C2H2}}) + ΔH^o_f(\ce{H2}) \right] \\ &= +52.3 \,kJ - \left[-226.8 \,kJ + 0\, kJ\right] \end{align} \nonumber \]

This is the sum of the enthalpies of formation of the products, multiplied by their stoichiometric coefficients (here, 1), minus the sum of the enthalpies of formation of the reactants, multiplied by their stoichiometric coefficients (here again, both 1). This is a general result, which we can summarize as

\[ΔH^o_{rxn} = \sum n_pΔH^o_p – \sum n_rΔH^o_r \nonumber \]

where \(n_p\) and \(n_r\) are the stoichiometric coefficients of each of the products and each of the reactants, respectively. [The \(\sum\) (Greek sigma) means “take the sum of”.] Note that this relationship can only be used if all the data are enthalpies of formation. For a general reaction

\[aA + bB \rightarrow cC + dD \nonumber \]

we would have

\[ΔH^o_{rxn} = \left[c ΔH^o_f(C) + d ΔH^o_f(D) \right] - \left[a ΔH^o_f(A) + bΔH^o_f(B)\right] \nonumber \]

Q2

Write the balanced thermochemical equations that pertain to the standard enthalpies of formation of the given compounds.

Compound	\(ΔH^o_f\, (kJ/mol)\)	Thermochemical Equation
\(\ce{CCl4(g)}\)	–106.7
\(\ce{Fe2O3(s)}\)	–822.16
\(\ce{HNO3(g)}\)	–134.31
\(\ce{NaHCO3(s)}\)	–947.7

Q3

Part A:

Given:

\[\ce{N_2O_4(g) + 1/2 O_2(g) \rightarrow N_2O_5(g)} \nonumber \]

with \(ΔH^o = +1.67 \,kJ\) and

\[ \ce{HNO_3(g) \rightarrow 1/2 N_2O_5(g) + 1/2 H_2O(l) } \nonumber \]

with \(ΔH^o = –2.96 \,kJ\).

Calculate \(ΔH^o\) for the reaction

\[\ce{N2O4(g) + H2O(l) + 1/2 O2(g) \rightarrow 2 HNO3(g) } \nonumber \]

Part B:

Given following standard enthalpy of formation data:

Compound	\(ΔH^o_f\, (kJ/mol)\)
\(\ce{N2O4(g)}\)	+9.66
\(\ce{HNO3(g)}\)	–134.31
\(\ce{H2O(l)}\)	–285.83

Calculate \(ΔH^o\) for the reaction

\[\ce{N2O4(g) + H2O(l) + 1/2 O2(g) \rightarrow 2 HNO3(g)} \nonumber \]

Compare your answer to your answer in Part A.

Q4

Calculate the heat of combustion of methane, CH₄(g), defined by the following thermochemical equation:

\[\ce{CH_4(g) + 2 O_2(g) \rightarrow CO_2(g) + 2 H_2O(l)} \nonumber \]

Given the following standard enthalpies of formation:

Compound	\(ΔH^o_f\, (kJ/mol)\)
\(\ce{CH4(g)}\)	–74.85
\(\ce{CO2(g)}\)	–393.5
\(\ce{H2O(l)}\)	–285.8 kJ

Q5

Calculate the enthalpy of formation, \(ΔH^o_f\), for benzene, \(\ce{C6H6(l)}\), given that the heats of formation of \(\ce{CO2(g)}\) and \(\ce{H2O(l)}\) are –393.5 kJ and –285.8 kJ, respectively, and that the heat of combustion of \(\ce{C6H6(l)}\) is –3267.7 kJ. To do this, carry out the following steps.

1. Write the balanced thermochemical equation that defines the enthalpy of formation of benzene, \(\ce{C6H6(l)}\).
2. Write the balanced thermochemical equation for the heat of combustion of benzene.
3. Based on your answer to question ii, write an expression for the heat of combustion of benzene, \(ΔH^o_{comb}\), in terms of the enthalpies of formation of the reactants and products. Using the data given in the problem, solve this for the unknown value of \(ΔH^o_f\) for benzene , the enthalpy of formation of benzene.

Electromagnetic Radiation

Light and other forms of radiant energy can be thought of a being propagated as a wave of oscillating electric and magnetic components. Hence, we call radiant energy electromagnetic radiation. Electromagnetic radiation is characterized by its energy (E), wavelength (\(λ\) – Greek lambda), and frequency (\(\nu\) – Greek nu). The speed of propagation in a vacuum, commonly called the speed of light (\(c\)), is \(2.9979 \times 10^8 m \,s^{–1}\). The relationships between \(E\), \(λ\), and \(\nu\) are

\[ \nu = \dfrac{c}{λ} \nonumber \]

\[E = h\nu = \dfrac{hc}{λ} \nonumber \]

where h is Plank’s constant, equal to 6.626 x 10^–34 J×s. These equations apply to all kinds of electromagnetic radiation. The units of wavelength are usually nanometers (nm), where 1 nm = 10^–9 m, although other length units may be used, depending on the radiation. An older unit called the Ångstrom (Å) is sometimes used with light and with x-rays, where 1 Å = 10^–10 m = 0.1 nm. Frequency usually has units of sec^–1, called the hertz (Hz). This means the number of waves that pass a reference point per second, but the word “wave” is not part of the unit and does not factor into the dimensional analysis.

The following chart shows the wavelength ranges of the various kinds of electromagnetic radiation.

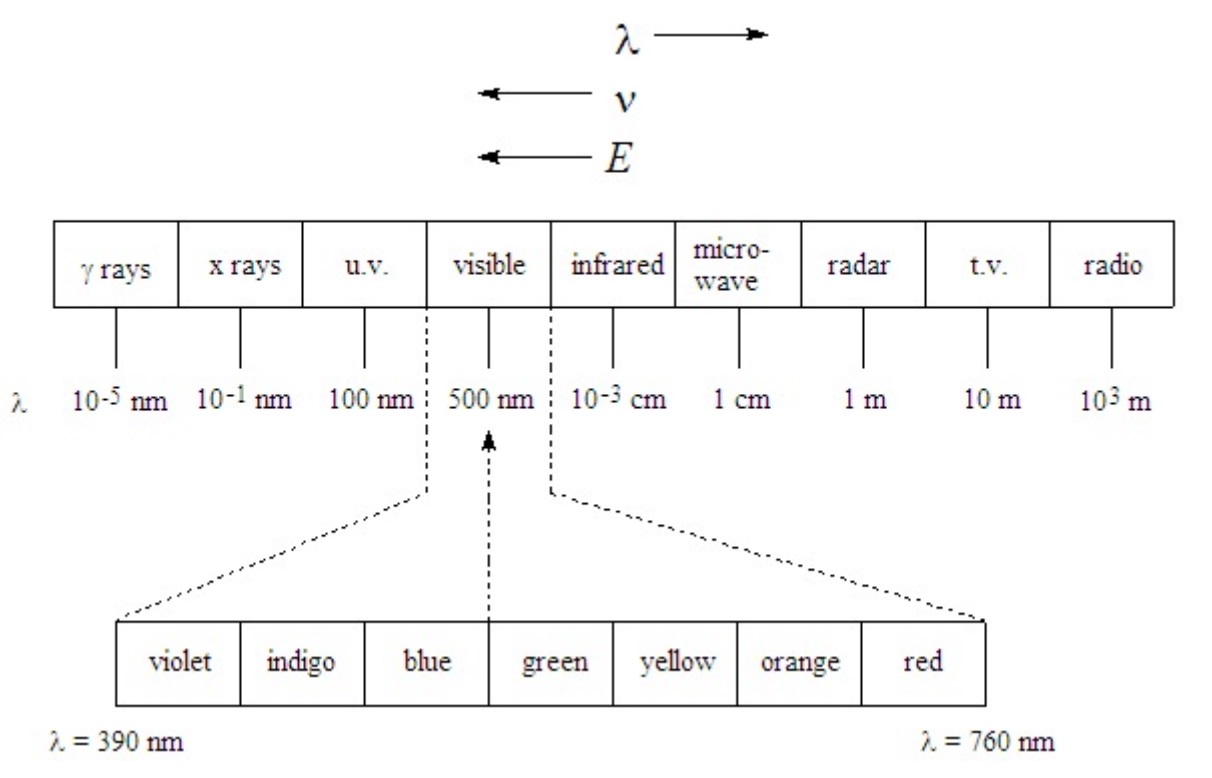
Q6

For each of the following, indicate which kind of radiation has higher energy.

1. red light vs. blue light
2. infrared radiation vs. radio waves
3. x-rays vs. visible light

Q7

For each of the following, indicate which has higher frequency

1. light with \(λ = 490\, nm\) vs. light with \(λ = 520\, nm\)
2. light with energy of \(3.0 \times 10^{–19} J\) vs. light with energy of \(4.5 \times 10^{–19} J\)

Q8

An argon laser emits green light with a wavelength of 514.5 nm. Calculate the following for this light: (a) the wavelength in Å; (b) the frequency in Hz (s^-1); (c) the energy in joules, J.

Line Spectra and the Bohr Model

Electrons bombarding hydrogen gas (H₂) in a discharge tube cause the formation of monatomic H atoms, some of which are in high energy states (excited states). The atoms can lose a portion of their excess energy by emitting electromagnetic radiation. Rather than a continuous spectrum containing all wavelengths within a range, the emitted radiation of hydrogen and other monatomic gasses consists of only certain characteristic wavelengths, which are typically observed as discrete lines in the spectrum, falling in the range from the ultraviolet region through the infrared region. Hence, these spectra are called line spectra. For hydrogen, four of these wavelengths fall in the visible region (where they can be seen by a human eye) and give lines that are violet (410 nm), blue (434 nm), blue-green (486 nm), and red (656 nm). In 1885, Balmer determined that these lines fit a relatively simple equation that relates the reciprocal of their wavelength (1/\(λ\)) to pairs of integers (\(n_1\) and \(n_2\)). When additional lines in the invisible infrared and ultraviolet regions were discovered, they and Balmer’s visible lines were all found to fit the following general equation:

\[ \dfrac{1}{\lambda} = R \left( \dfrac{1}{n_1^2} - \dfrac{1}{n_2^2} \right) \nonumber \]

with \(n = 1, 2 ,3\, \ldots \infty\) and \(n_2 > n_1\).

where \(R\), the Rydberg constant, is \(1.096776 \times 10^{7} m^{-1}\), and the \(n\) values are integers with \(n_2 > n_1\). This equation was only valid for the emissions from hydrogen, a one-electron atom. In the case of the visible lines of the Balmer series, the value of \(n\) is 2. When \(n = 1\), the associated lines 1 fall in the ultraviolet region (the Lyman series). Values of \(n \ge 3\) correspond to successive series that fall in the infrared region (the Paschen, Brackett, and Pfund series), with increasing wavelength and decreasing frequency and energy as \(n\) increases.

Neils Bohr, inspired by the Balmer equation and Max Plank’s ideas of quantized energy, devised a model for the hydrogen atom. In Bohr’s model the single electron is thought to be confined to certain orbits around the nucleus, where each orbit corresponds to a particular, quantized energy, given by the equation

\[ \dfrac{1}{\lambda} = -hcR \left( \dfrac{1}{n^2} \right) = (-2.18 \times 10^{-18} J) \left( \dfrac{1}{n^2} \right) \nonumber \]

Here \(n\), the principal quantum number, can take on integer values from 1 to 4. This equation can be extended to other one-electron atoms (e.g., \(\ce{He^{+}}\), \(\ce{Li^{2+}}\)) in the form

\[E_n = \dfrac{-BZ^2}{n^2} \nonumber \]

with

• \(n = 1, 2 ,3\, \ldots \infty\)
• \(B\) is a constant similar to the Rydberg constant and
• \(Z\) is the atomic number (number of protons).

In either form, the Bohr equation predicts that the energy of the one-electron atom is inversely proportional to the square of the quantum number of its state. This gives rise to the energy level diagram shown on the last page of this work sheet, in which the spacing between energy states gets smaller as \(n\) increases.

In Bohr’s model, as \(n\) increases, the electron is in an orbit that is further from the nucleus and therefore has a higher (less negative) energy. Note that the zero of energy corresponds to n = 4, which has the electron an infinite distance away from the nucleus. Any lower value of n places the negative electron closer to the positive nucleus to which it is attracted, giving rise to a more favorable (negative) energy. The atom absorbs or emits energy in the form of electromagnetic radiation by changing from an initial state (\(E_i\)) with a value n to a final state (\(E_f\)) with a value \(n\). These changes in state are called transitions. With absorption, the atom acquires energy, resulting in a higher energy state. Thus, for an absorption transition, \(n_f > n_i\). With emission, the atom loses energy, resulting in a lower energy state. Thus, for emission, \(n_f < n_1\). It is transitions from higher energy states to lower energy states that give rise to the observed line spectra. For any transition, the energy of the electromagnetic radiation (a photon) absorbed or emitted must exactly match the energy difference between the two states; i.e.,

\[\Delta E = E_f – E_i = E_{photon} = h\nu \nonumber \]

Using the Bohr equation for the allowed energies in states \(n_f\) and \(n_i\), we can write an equation to calculate the photon’s energy as

This equation has the same form as the experimentally determined Balmer equation, if we assume nf i 1 2 and n of the Bohr equation correspond to n and n of the Balmer equation. Regardless of whether absorption or emission is involved, the energy of a photon is always taken as a positive number, so any sense of sign to the energy calculated from this equation is routinely dropped.

As the diagram on the last page shows, the Balmer series, which gives rise to the four lines in the visible spectrum, corresponds to transitions from higher states down to \(n_f = 2\) (i.e., \(3 \rightarrow 2\), \(4 \rightarrow 2\), \(5 \rightarrow 2\), \(6 \rightarrow 2\)). The energy gaps between \(n_f = 2\) and \(n_i > 2\) are such that the wavelengths of the emitted photons fall in the visible region. In the Lyman series (see diagram), the transitions are f from upper states down to the lowest state (\(n_f = 1\)), called the ground state of the atom. The gaps between \(n = 1\) and \(n > 1\) states are bigger, and so the emitted photons have higher energies, falling in the ultraviolet region. By contrast, in the Paschen series (see diagram), the transitions are f from higher states down to \(n_f = 3\). Because the energy separations between states with higher n values are smaller, the transitions have lower energies, falling in the infrared region. The energy f differences are even smaller when the transitions are from upper states to either \(n_f = 4\) or \(n_f = 5\), making the emitted radiation fall even further into the infrared region for these series (see Brackett and Pfund series on the diagram).

Q9

Is energy emitted or absorbed when the following transitions occur in hydrogen: (a) from \(n = 1\) to \(n = 3\), (b) from \(n = 5\) to \(n = 2\), (c) an \(\ce{H^{+}}\) ion acquires an electron into the \(n = 2\) state.

Q10

The four visible lines of the Balmer series in the emission spectrum of hydrogen are violet (410 nm), blue (434 nm), blue-green (486 nm), and red (656 nm). Assign these as state-to-state transitions of the type \(n_i \rightarrow n_f\), giving the \(n\) values involved for each line.

Q11

Calculate the energy of the first line in the Lyman series for the hydrogen atom, which arises from a transition from \(n_i = 2\) to \(n_f = 1\). What is the wavelength of the radiation emitted? In what region of the electromagnetic spectrum does it fall?