2B: Gas Laws II (Worksheet)
- Page ID
- 81614
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Name: ______________________________
Section: _____________________________
Student ID#:__________________________
Work in groups on these problems. You should try to answer the questions without referring to your textbook. If you get stuck, try asking another group for help.
The fundamental relationship PV = nRT can be extended to understand the densities of gases under various conditions and to understand how non-reacting gases behave when mixed together. This and all of the behaviors represented by PV = nRT can be understood on the basis of a model called the Kinetic Molecular Theory.
Learning Objectives
- Understand the relationships between gas parameters and gas density
- Understand how molecular weight is related to the parameters of a gas
- Understand Dalton’s Law and the concept of partial pressures in a gas mixture
- Understand the fundamental tenants of Kinetic Molecular Theory
- Understand the relationship between Kinetic Molecular Theory and Graham’s Law of Effusion
Success Criteria
- Be able t°Calculate density of a gas from pressure, temperature, and molar mass data
- Be able t°Calculate molar mass of a gas from P, V, T, and sample mass data
- Be able t°Carry out partial pressure calculations
- Be able t°Calculate molecular velocities and kinetic energies of gases
- Be able to apply Graham’s Law to predict rates of effusion and molar masses of gases
Useful Constants
- R = 0.08206 L×atm/K×mol K = oC + 273.15
Gas Densities
From PV = nRT we can see that if two gas samples have the same pressure, volume, and temperature, they must have the same number of moles. This is Avogadro’s hypothesis. But if the two gases are chemically different, the masses of the samples will be different. This means that their densities must be different, too. Recall that density is mass per volume, so if the volumes are the same the densities are proportional to the molecular masses of the gases. From your book or the lecture you may have seen that density of a gas can be calculated from the equation,
\[d = \dfrac{PM}{RT} \nonumber \]
where M is the molar mass. But it is unnecessary to memorize this equation. Just calculate the volume of one mole of the gas from \(V = nRT/P\), and then divide the result into the known molar mass.
Q1
Taking a breath of He(g) makes your voice sound like Mickey Mouse. Taking a breath of \(SF_6(g)\) makes your voice sound like Darth Vader. Explain the difference.
Q2
What is the density of methane gas (m.w. = 16.04 u) at 3.00 atm when the temperature is 32 °C?
Calculating Molar Mass from Gas Data
From your book or the lectures you may have seen the following equation for calculating the molar mass of a sample gas from P, V, T data:
\[ M = \dfrac{mRT}{RT} \nonumber \]
where \(m\) is the sample’s mass in grams. As with the special equation for density, it is not necessary to memorize this equation. With P, V, T data for a gas sample whose mass is known, simply calculate the number of moles, n, for the sample. The molar mass, then, is the sample mass divided by the number of moles. Don’t waste your time memorizing these useless special equations! All you need is PV = nRT.
Q3
A 1.365-g sample of a pure, unknown gas in a 1.000-L vessel at 22.15 °C has a pressure of 965.4 torr. What is the molar mass of the gas?
Partial Pressures and Dalton’s Law
In a mixture of gases, each gas behaves as if it alone occupied the entire volume. Therefore, we can assign a pressure to each gas in a mixture, called its partial pressure, pi . Dalton's Law sates that the total pressure of a gas mixture is the sum of the partial pressures of all its component gases; i.e.,
\[P_t = p_1 + p_2 + \ldots + p_n = \sum_i p_i \nonumber \]
For a mixture in a fixed volume at constant temperature, by \(PV = nRT\) the total pressure is proportional to the total number of moles of all the gases, \(n_{tot}\). Likewise, the partial pressure from an individual gas in the mixture, say gas \(A\), is proportional to its number of moles, \(n_A\). If we define the mole fraction of A as \(\chi_A = n_A/n_t\), then from the proportionality between moles and pressures it follows that
\[\chi_A = \dfrac{p_A}{p_{tot}}. \nonumber \]
We can write a similar expression for every component gas in the mixture, so
\[\chi_A + \chi_B + ... = \sum_i x_i = 1 \nonumber \]
In other words, the sum of all the mole fractions, which can be calculated from either the moles or pressures, adds up to one. support tray water bath water filled bottle gas sample displacing water water level gas producing reaction
Q4
A mixture containing 0.226 mol He, 0.342 mol Ne, and 0.128 mol Ar is confined in a 4.00- L vessel at 25 °C.
- What is the total pressure of the gas?
- What are the mole fractions of all the gases in the mixture?
- What is the partial pressure of each gas in the mixture?
- What is the sum of the partial pressures. How does it compare to the total pressure you calculated in part i. Explain any difference.
Collecting a Gas Over Water
Sometimes in the laboratory we collect a gas by displacement of water from an inverted water filled bottle.
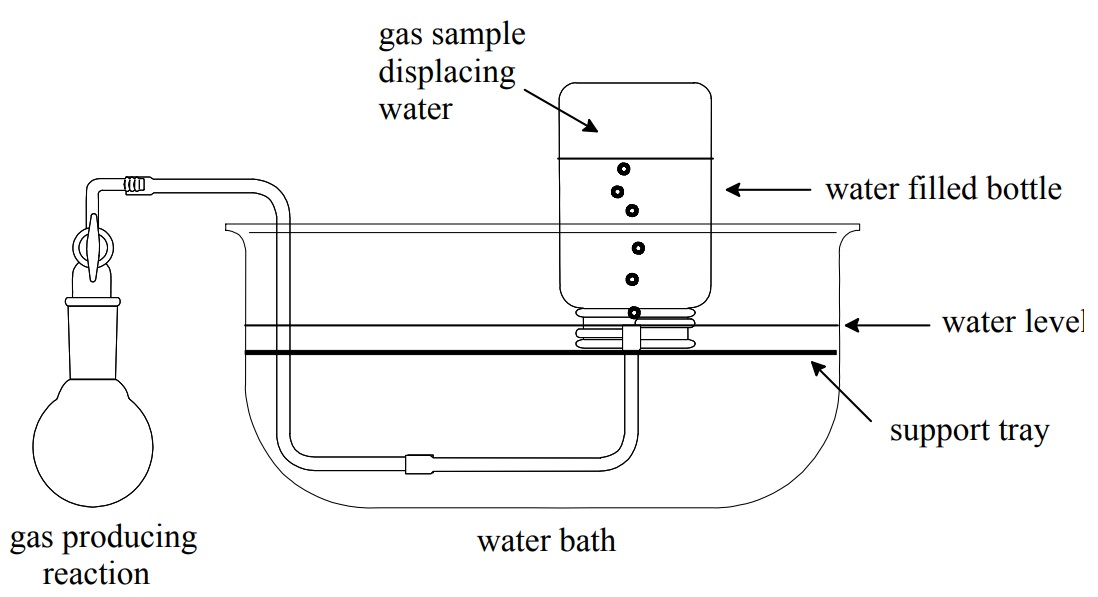
A sample collected in this way contains the gas of interest and water vapor; i.e., it is a gas mixture. When the collected gas expels all the water from the bottle, the sample's pressure is the same as the atmospheric pressure in the laboratory. Therefore, the total pressure of the sample is
\[P_{toy} = p_{gas} + p_{wv} = P_{atm} \nonumber \]
To determine the partial pressure of the gas, the vapor pressure of water at the temperature of the sample must be subtracted from the observed total pressure,
\[P_{tot} = P_{atm}. \nonumber \]
Values of vapor pressure of water at various temperatures are tabulated in standard chemical handbooks.
Q5.
A 97.6-mL sample of hydrogen gas is collected by water displacement at 20.0 °C. The atmospheric pressure in the laboratory is measured to be 769.5 torr. How many milligrams of hydrogen does the sample contain? The tabulated value of the vapor pressure of water at 20.0 °C is 17.5 torr.
Kinetic Molecular Theory
The observed behavior of gases, as expressed by the empirical gas laws, can be understood on the basis of the kinetic molecular theory, which developed over many years up to 1857, when Rudolf Clausius (1822-1888) published it in its most complete and elegant form. This theory is based on the following assumed model of the nature of a gas sample.
- No attractive forces exist between gas molecules.
- Molecules' volumes are negligible compared to the volume of the gas sample as a whole.
- Gas molecules are in constant, rapid, straight-line motion.
- Collisions between molecules or the container walls are elastic; i.e., no loss of kinetic energy or momentum.
- Gas pressure arises from molecules striking the walls of the container.
- The average kinetic energy is proportional to the absolute temperature.
From these considerations, it can be shown that for one mole of ideal gas, the root-mean squared velocity, \(v_{rms}\), is
\[ v_{rms} = \sqrt{\dfrac{3RT}{M}} \label{rms} \]
where
- R = 8.3143 J/K mol (gas constant in joules)
- T = temperature in kelvin (K)
- M = molar mass in kg mol-1
Because kinetic energy is proportional to velocity squared, the average kinetic energy of the population of molecules is proportional to the average of the squares of all the individual velocities; i.e., \(v_{rms}^2\). Using the defintions of \(v_{rms}\) from Equation \ref{rms}, the mean kinetic energy, \(\overline{KE}\), for a mole of ideal gas,is
\[\overline{KE} = \dfrac{1}{2} Mv^2_{rms} = \dfrac{1}{2} \left( \sqrt{\dfrac{3RT}{M}} \right)^2 \nonumber \]
is
\[\overline{KE} = \dfrac{3}{2} RT \label{eq5} \]
Note that Equation \ref{eq5} indicates that the mean kinetic energy of the gas molecules is proportional to absolute temperature, and has nothing to do with the identity of the gas molecules, including molecular mass.
Q6
Two gas tanks have the same volume. One containing \(N_2(g)\) at 25 °C has a pressure 25 atm. The other containing \(CO_2 (g)\) at 0 °C has a pressure of 50 atm.
- Which vessel has more molecules of gas?
- In which tank is the root-mean-squared (rms) velocity of molecules higher?
- In which tank is the average kinetic energy of the molecules higher?
Graham’s Law of Effusion
Effusion is the escape of a gas from a pinhole leak (an orifice) in a container. The rate of escape is related to the speed of the molecules – faster molecules move more quickly and slower molecules move more slowly. As we have seen from the kinetic molecular theory, the rms velocity is directly proportional to the square root of the absolute temperature and inversely proportional to the square root of the molar mass. If we compare the escape of two different gases from identical apparatus under constant temperature and pressure conditions, their relative rates of effusion will be inversely proportional to the square root of the ratio of their molar masses:
\[ \dfrac{r_A}{r_B} = \sqrt{\dfrac{M_B}{M_A}} \nonumber \]
Q7
If 3.62 mL of an unknown gas effuses in the same time it takes 6.91 mL of argon (at. wt. = 39.95 u) from identical apparatus, what is the molar mass of the unknown gas?


