1B: Gas Laws - Part 1 (Worksheet)

Name: ______________________________

Section: _____________________________

Student ID#:__________________________

Work in groups on these problems. You should try to answer the questions without referring to your textbook. If you get stuck, try asking another group for help.

Of the three principal states of matter (gas, liquid, solid), gases show behavior that is most easily connected to molecular motion. The observed behavior of gases, embodied in the empirical gas laws, leads to a series of equations that can be summarized by a single equation of state, called the ideal gas law equation. This shows the relationship between a gas’s pressure (P), temperature (T), volume (V), and amount in moles (n). Connecting these variables together is a fundamental constant of the universe, called the gas constant (R).

Learning Objectives

• Understand the nature of the parameters that define the behavior of gases
• Know the names and relationships represented by the various empirical gas laws
• Understand the meaning of the ideal gas law
• Know how to extract the relevant relationship from the ideal gas law to predict the values of gas parameters when sample conditions are changed
• Know standard temperature and pressure (STP)

Success Criteria

• Be able to calculate pressure from fundamental equations of physics
• Be able to determine pressure from barometer and manometer readings
• Be able to carry out various empirical gas law calculations
• Be able to apply the ideal gas law
• Be able to use STP in gas-law calculations, when appropriate

Defining Pressure

A sample of gas is characterized by specifying its amount, its temperature, its volume, and its pressure. Most of us have a clear idea about the first three parameters, but our understanding of pressure may be less precise. In physics, pressure is defined as force applied per unit of area,

\[P = \dfrac{F}{A} \nonumber \]

Force is defined as the product of mass times acceleration, \(F = ma\).

Q1

Using SI units of kilograms, meters, and seconds with these fundamental equations, determine the combination of units that define the following:

1. The newton (N), the fundamental unit of force
2. The pascal (Pa), the fundamental unit of pressure

Measuring Air Pressure

Historically, air pressure has been measured by observing the height of the column in a mercury barometer.

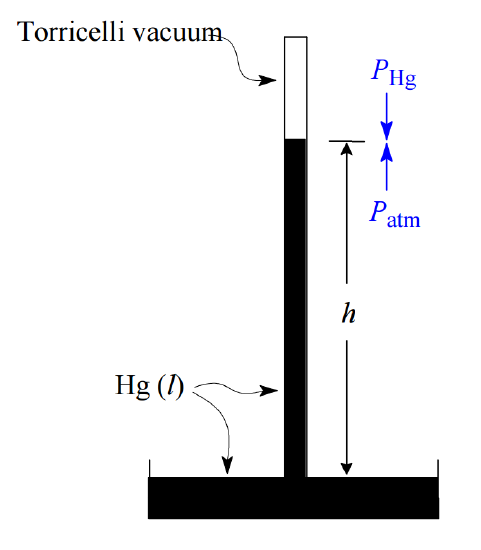
When the downward pressure of the mercury in the closed column exactly equals the air pressure on the surface of the mercury pool into which the open end of the tube is submerged, a stable level is achieved whose height can be used as an indication of the air pressure. In these terms we define one standard atmosphere (1 atm) as the pressure required to sustain a 760-mm height of mercury, written 760 mm Hg. The unit of mm Hg is also called the torr, so 1 atm = 760 torr.

Q2

The pressure of a column of liquid is given by \(P = gdh\), where g is the acceleration of gravity (9.807 m×s^–2), d is the density, and h is the height. The density of mercury is 13.6 g/cm³. What is the pressure in Pa exerted by a 760-mm column of mercury?

Q3

In the United States we quote barometric pressure in inches of mercury (in. Hg). What is one standard atmosphere of pressure in these units? (1 in. º 2.54 cm)

Q4

In Europe barometric pressure is quoted in hectopascals (hPa), where hecto means one hundred. What is one standard atmosphere in hPa?

Q5

A typical 10W-40 motor oil has a density of 0.875 g/cm³. If you were to construct a barometer using 10W-40 motor oil, how high would the column be when the pressure is one atmosphere?

Measuring Sample Gas Pressure - Manometers

Sample gas pressures are measured using the height difference in the U-tube of a manometer. Manometers are either closed-end or open-end in design.

A closed-end manometer (above, left) gives an absolute measure of the pressure in torr; the open-end manometer (above, right) gives the pressure relative to the atmospheric pressure on the open end. To use an open-ended manometer, one must also know the barometric pressure at the time of the reading.

Q6

Refer to the pictures of closed- and open-ended manometers above.

1. In the manometer on the left, the left side reads 108 mm and the right side reads 32 mm. What is the pressure of the sample gas in torr?
2. In the manometer on the right, the left (outer) side reads 98.3 mm, and the right (inner) side reads 32.1 mm. The pressure in the laboratory is 756.2 mm Hg. What is the pressure of the sample gas in torr?
3. In the manometer on the right, if the heights of the two sides were reversed (32.1 mm on the left and 98.3 mm on the right), what would the pressure of the sample gas be in torr?

Empirical Gas Laws - Boyle’s Law

Boyle’s Law says that for a sample of gas at constant temperature the volume is inversely proportional to the pressure.

Q7

Carry out the following steps to derive equations for Boyle’s Law.

1. Express Boyle’s Law as a proportion between \(V\) and \(P\).
2. A proportionality can be changed into an equation by adding a proportionality constant. For example, if \(y \propto x\), we can use a constant, \(c\), to write the equation \(y = cx\). Do this for the Boyle’s Law proportionality you just wrote, making b be the constant.
3. Under what conditions is b a constant?
4. Consider a gas sample at constant temperature with an initial volume V1 and an initial pressure P1. Write an equation that shows how \(V_1\) and \(P_1\) are related to new volume and pressure conditions, \(V_2\) and \(P_2\), if either is changed. [Hint: look at the equation you wrote in part ii.]

Q8

A 144-mL sample of gas in a piston chamber has a pressure of 2.25 atm. If the piston is pushed in so that the gas has a volume of 36.0 mL, what is the new pressure? Assume the temperature remains constant.

Empirical Gas Laws - Charles’ Law

Charles’ Law says at constant pressure the volume occupied by a given amount of gas is directly proportional to its absolute temperature.

Q9

Carry out the following steps to derive equations for Charles’ Law.

1. Write a proportionality between \(V\) and \(T\) that expresses Charles’ Law.
2. Using the proportionality constant c, write an equation for the relationship between \(V\) and \(T\).
3. Under what conditions is c a constant?
4. What does “absolute temperature” mean? Why must we use absolute temperature in the equation for Charles’ Law?
5. Write an equation for the relationship between initial temperature and volume, \(T_1\) and \(V_1\), and final temperature and volume, \(T_2\) and \(V_2\), when either of these is changed under constant pressure conditions.

Q10

A 5.00-L sample of gas in a piston chamber at 25 °C is heated to 100 °C, while the pressure is maintained at 1.00 atm. What is the volume of the gas after heating?

Empirical Gas Laws - Combined Gas Law

Boyle’s Law and Charles’ Law can be combined into one equation that expresses the volume, temperature, and pressure relationships for a fixed amount of gas.

Q11

Carry out the following steps to derive equations for the Combined Gas Law.

1. Combine your two proportionality expressions for Boyle’s Law and for Charles’ Law into one expression that shows how volume depends on both pressure and temperature.
2. Using the proportionality constant k, write an equation for this combined gas law.
3. Write an equation for the relationship between initial conditions \(V_1\), \(P_1\), and \(T_1\) and final conditions \(V_2\), \(P_2\), and \(T_2\), when any two of these are changed for a sample of gas.

Q12

At 29 °C and 756 torr, a gas occupies 2.50 L. What is the volume if the temperature is changed to 159 °C, and the pressure is changed to 1550 torr?

Ideal Gas Law

For any sample of gas under ideal conditions, the relationship between the amount of gas in moles (n) and its temperature, pressure, and volume is given by the relationship

\[PV = nRT \nonumber \]

in which R is the gas constant, with a value of 0.08206 L×atm/K×mol. When using this value of R, volume must be in liters, temperature must be in degrees kelvin, and amount of gas must be in moles. If other units are given, convert to these units. When other units are used, the value of R is different. [Later, we will see another use of R, where its value and units are 8.314 J/K×mol.]

Q13

A sample of He(g) occupies 15.0 L with a pressure of 856 torr when the temperature is 52 ^oC. How many grams of He(g) does the sample contain? [at. wt. He = 4.00 u]

Seeing Gas Law Relationships in PV = nRT

We have seen equations for Boyle’s Law, Charles’ Law, and the Combined Gas Law. You really do not need to remember these equations if you know PV = nRT, because these and some other relationships we have not seen yet are contained in the ideal gas law. For example, Boyle’s Law is the relationship between volume and pressure when amount and temperature are constant. If we take the variable n and T in PV = nRT as constants, then everything on the right is a constant. The product of any number of constants is a constant, so we could write

\[PV = nRT = b \nonumber \]

where b = nRT. The resulting equation, PV = b, is our previous equation for Boyle’s Law.

Q14

Derive the equation for Charles’ Law by rearranging PV = nRT to put all the constants on one side of the equation. Then, redefine the product of the constants to be the constant c.

Q15

Amonton’s Law expresses the relationship between temperature and pressure for a gas sample under constant volume. Derive the expression for Amonton’s Law, using a as a constant. Then write the relationship between initial conditions T₁ and P₁ and final conditions T₂ and P₂, when amount and volume are constant.

Q16

Avogadro’s Law is based on the relationship between the amount of gas and its volume under constant temperature and pressure conditions. Derive an equation for Avogadro’s Law from PV = nRT to show the relationship between initial conditions n₁ and V₁ and final conditions n₂ and V₂.

Q17

Avogadro’s Law was an extension of an earlier observation of Gay-Lussac. Gay-Lussac’s Law says that in reactions between gases at constant temperature and pressure, the volumes that react are in the ratios of small whole numbers. Nitrogen gas and hydrogen gas combine directly to form ammonia gas. Write the balanced equation for this reaction. If 250 mL of nitrogen gas at 5.00 atm and 750 K is reacted with hydrogen gas at the same pressure and temperature, what volume of hydrogen gas is required? What is the theoretical yield in milliliters of ammonia gas under these conditions?

Standard Temperature and Pressure

Because of PV = nRT, we can calculate the volume occupied by one mole of gas under specific temperature and pressure conditions. For convenience, we define Standard Temperature and Pressure (abbreviated STP) as 0 °C (273 K) and 1 atm. Using these values in PV = nRT, we can calculate the molar volume at STP for an ideal gas:

1 mol gas = 22.4 L

Realize that this relationship is valid only when the sample of gas is at STP conditions.

Q18

What volume at STP does a 76.0-g sample of N₂ (m.w. = 28.0 u) occupy?

Q19

A gas sample with a mass of 57.2 g at STP occupies 80.0 L. Which of the following gases might it be: N₂, CO₂, CH₄?