Solutions Preparation and Dilutions

Learning Goals:

• To be able to choose appropriate glassware for solution preparation
• To be able to demonstrate proper solution preparation
• To be able to dilute and recalculate the original concentration of solution

Analytical Glassware and Tolerance

A variety of glassware exists in the laboratory to perform a variety of tasks.  Just like one would use a screwdriver for some tasks and a hammer for others, chemists need to make choices about what glassware is appropriate for carrying out certain tasks in the laboratory.  The two types of measurements one normally makes in the lab are measures of mass or volume.  A variety of glassware is available for making these transfers, but it is important to know the limitations of each piece of glassware one uses because it contributes to the overall error associated with the measurement.

Mass Measurements

Two types of balances exist for making mass measurements, top-loading or analytical balances.  Top-loading balances are used to make measurements of large masses (> 1 g) while analytical balances are routinely used to make measurements of small masses (< 1 g). For the purposes of our lab, we will mostly be using the analytical balance, shown below. Before using the balance, it must be clean and level. Typical analytical balances can measure to ± 0.1 mg.  All balances have an upper limit to which they can measure.

 

Figure 1.  Analytical balance from Harvey Analytical Chemistry 2.1

Volume Measurements

Many types of glassware exist for transferring or storing liquids in the laboratory, but there is a big difference in their accuracy and precision.  The tolerance of a piece of glassware is a term that denotes the permissible range from the true value that the glassware can deliver.  In general, beakers < graduated cylinders < volumetric pipets for delivering volumes, and beakers < graduated cylinders < volumetric flasks for containing volumes. The tolerance of glassware varies with the volume being delivered, and the greatest error always arises when trying to transfer small versus large volumes.

Problem 1 (from Analytical Chemistry: A Guided Inquiry Approach, Wiley, 2014)

Tolerance is the permissible deviation from a specified value for a particular piece of glassware.  All glassware has some tolerance for accuracy.  That is, all glassware contains or delivers volumes that can be slightly different from the stated volume that is printed on the glassware.  The tolerance is well-documented for each type and volume of glassware.

Volumetric flasks are calibrated by a manufacturer to contain a specific volume.  Volumetric flasks are marked with “TC” indicating “to contain” that volume at a stated temperature.  The tolerances for KIMAX Brand Volumetric Flasks, Class A, are given in the table below:

Capacity, mL	Tolerance, ± mL	% Relative Tolerance	Minimum Volume	Maximum Volume
10	0.02
25	0.03
50	0.05	0.10
100	0.08	0.08
200	0.10	0.05
250	0.12
500	0.20	0.04
1000	0.30	0.03
2000	0.50

1. Calculate the missing % relative tolerances for the 10, 25, 250, and 2000 mL flasks.
2. Calculate the minimum and maximum volumes that can be contained in all of these flasks.
3. Compare the % relative tolerance for the different size volumetric flasks. What happens to the % relative tolerance as the volume of the flask increases?
4. For optimal accuracy, would you recommend using a larger or smaller sized flask? Explain your reasoning.

Making Solutions

Last class, we saw how there are many more concentrations units than just molarity, and you also determined how to calculate the amount of solute, solvent, and solution and how to interconvert between units.  Today we are going to think more deeply about how you would physically prepare solutions of a specified concentration (called stock solutions), and then how one could make dilutions from stock solutions to prepare a series of working standards (called standard solutions).  You will be doing this almost every laboratory period, so you need to become comfortable doing this. 

Problem 2

Describe how to prepare the following solutions starting from the following reagents:

• 500 mL of 0.20 M NaOH using solid NaOH
• 1 L of 150.0 ppm Cu²⁺ using solid Cu metal
• 2L of 4% v/v acetic acid using concentrated glacial acetic acid (99.8% w/w acetic acid)
• 1 L of 100.0 ppm NaCl solution starting from solid NaCl
• 1 L of 100.0 ppm SO₄^2- solution starting from solid Na₂SO₄

Problem 3

Calculate the molarity of:

• 1 L of 100.0 ppm NaCl solution
• 1 L of 100.0 ppm SO₄^2- solution starting from solid Na₂SO₄

Problem 4

The density of concentrated ammonia, which is 28.0% w/w NH₃, is 0.899 g/mL. What volume of this reagent should you dilute to 1.0 × 10³ mL to make a solution that is 0.036 M in NH₃?

Dilution Calculations

Standard solutions used for making calibration curves are often prepared by diluting a more concentrated stock solution. A known volume of the stock solution is transferred to a new container and brought to a new volume. Since the total amount of solute is the same before and after dilution, we know that:

\[C_o × V_o = C_D × V_D\nonumber\]

where C_o is the stock solution’s concentration, V_o is the volume of stock solution being diluted, C_d is the dilute solution’s concentration, and V_d is the volume of the dilute solution.  The type of glassware used to measure V_o and V_d depends on how precisely we need to know the solution’s concentration

Problem 5

A series of dilute NaCl solutions are prepared starting from a stock solution of 0.100 M NaCl. Solution A is prepared by pipeting 10 mL of the stock solution into a 250-mL volumetric fask and diluting to volume. Solution B is prepared by pipeting 25 mL of solution A into a 100-mL volumetric fask and diluting to volume. Solution C is prepared by pipeting 20 mL of solution B into a 500-mL volumetric flask and diluting to volume. What is the molar concentration of NaCl in solutions A, B and C?

Problem 6

A laboratory procedure calls for 250 mL of an approximately 0.10 M solution of NH₃. Describe how you would prepare this solution using a stock solution of concentrated NH₃ (14.8 M).

Problem 7

A student digests a 4.235 g mass of paint suspected of containing lead in acid and allows the sample to heat overnight to dissolve.  In the morning, the student returns to filter the sample, and the acid solution containing the lead is diluted to the mark in a 100.00 ml volumetric flask.  The student decides to analyze the solution using an external calibration curve and AAS.  She prepares and measures a series of calibration standards and obtains the following graph.  She next measures her sample absorbance and obtains a value of 1.020.  What would her next move be?

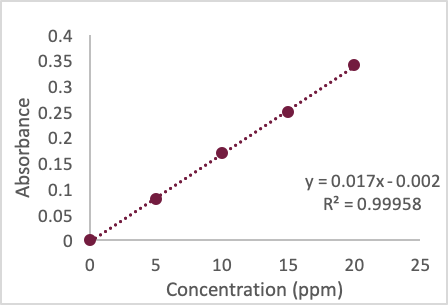
Suppose the student decides to dilute her original sample by a factor of 5 (she dilutes a 5.00-mL aliquot into a 25.00 mL volumetric flask and dilutes to the mark with water) and obtains an absorbance of 0.321.  What is the concentration of Pb in the flask (with units)?

The student wants to relate the diluted concentration of Pb measured in her flask back to the original mass of paint extracted.  How would she do this?  Show your work.

Problem 8

The following graph is an external standard calibration plot for the cold vapor atomic absorption determination of mercury in sea water. The sea water sample was prepared by dilution of the original sample (20.00 mL sea water diluted to 100.0 mL with nanopure water). The dilute sample had an absorbance reading of 0.40. Use the graph to estimate the concentration of Hg in the original sea water sample.

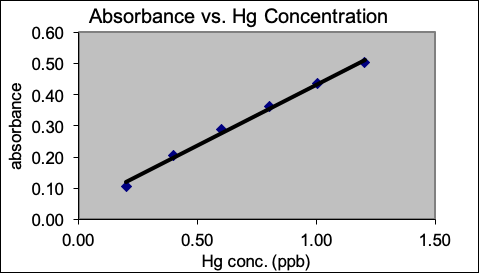
1. ~1 ppb
2. ~5 ppb
3. ~0.2 ppb
4. ~2 ppb
5. Insufficient data

Problem 9

To prepare a standard solution of Zn²⁺ you first dissolve a 1.004 g sample of Zn wire in a minimal amount of HCl and dilute to volume in a 500-mL volumetric flask to make the stock solution. Next, you dilute 2.000 mL of this stock solution to 250.0 mL. What is the concentration of Zn²⁺, in µg/mL, in your standard solution?

Problem 10

A sample of an ore was analyzed for Cu²⁺ as follows. A 1.25 g sample of the ore was dissolved in acid and diluted to volume in a 250-mL volumetric flask. A 20-mL portion of the resulting solution was transferred by pipet to a 50-mL volumetric flask and diluted to volume. An analysis of this solution gives the concentration of Cu²⁺ as 4.62 µg/L. What is the weight percent of Cu in the original ore (in g Cu per g of ore)?

Contributors and Attributions

• Amy Witter, Dickinson College ([e-mail])
• Sourced from the Analytical Sciences Digital Library