Skip to main content
Chemistry LibreTexts

Quantitative Analysis: Nuts and Bolts

  1. Last updated
  2. Save as PDF
  • Page ID
    278755

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    The second unit of this course is built on the foundations of equilibrium. Which will be utilized in titrations, gravimetric, and combustion analysis techniques to quantify an analyte. We must remember that this builds off of the quality controls, statistics, and error minimization from unit one.

    Objectives

    By the end of this students should be able to:

    1. Understand the different forms of quantification techniques presented, including multiple titrations, gravimetric analysis, and combustion analysis.
    2. Perform calculation on all of the aforementioned methods to determine the quantity of an analyte.
    3. Perform all of the quality control and statistical analysis of the presented methods to determine their absolute and relative quality.

    Equilibrium Review

    Reading: Chapter 1 (section 5), Exploring Chemical Analysis 5th ed., D. Harris 

    Memorize the table 8-1 of common strong acids and bases in your book.

    Equilibrium Constant

    \[aA+bB⇆cC+dD\nonumber\]

    \[K= \dfrac{[C]^c [D]^d}{[A]^a [B]^b}\nonumber\]

    • How do you define equilibrium?

     

     

    • What does K tell us?

     

     

    • What is excluded from the K expression?

     

     

    STOP

    • Consider the reaction above. Assume that the value of the equilibrium constant is very large.
      1. Which species predominate at equilibrium, reactants or products?

         

      2. Which reaction has the larger rate constant, the forward or the reverse?

     

     

    STOP

     Types of Titrations. 1: Direct Titration (1 step). Analyte + Titrant → Product. 2: Back Titration (at least 2 steps). Analyte + Reagent 1 → Product + Excess Reagent 1. Excess Reagent 1 + Reagent 2 → Product. 3: Gravimetric Titration. Titrant measured by mass. Concentration given as (moles reagent)/(kg of solution) Why would we use this type of titration?

     

    Titration Basics

    Reading: Chapter 6 (sections 1-3), Exploring Chemical Analysis 5th ed., D. Harris 

    equivalence_vs_endpoint.png

    Discuss as a group the following questions

    • When is the solution clear?

     

     

    • When does the solution turn purple?

     

     

    • What error does this introduce?

     

     

    • State in your own words the diff b/t equivalence point and end point.

     

     

     

    STOP

    To account for the difference between equivalence and end point we can measure a blank titration. The volume required to produce the same noticeable change without the presence of the analyte is subtracted from subsequent titrations.

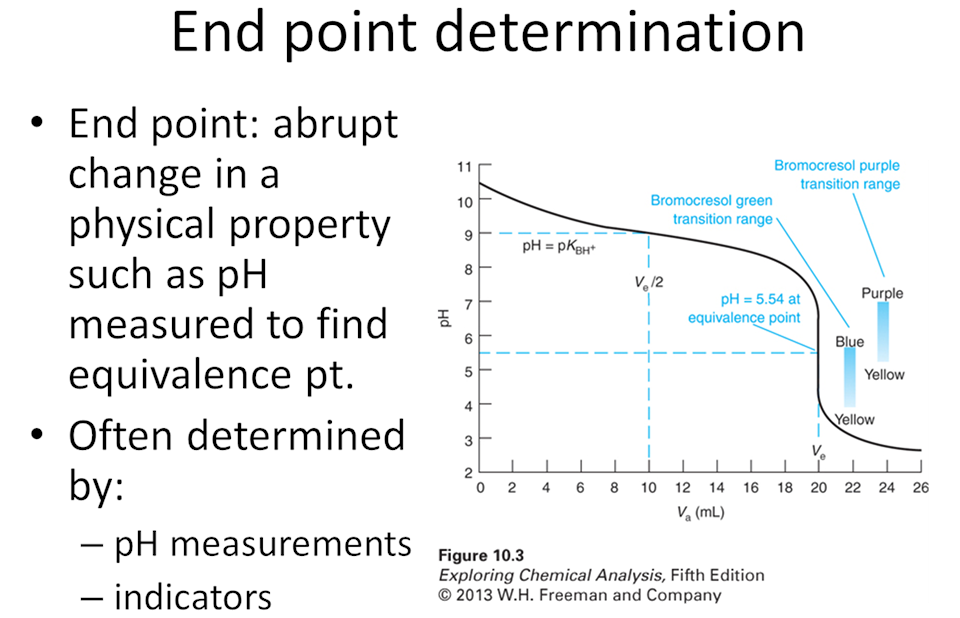
    Fig10.3.png

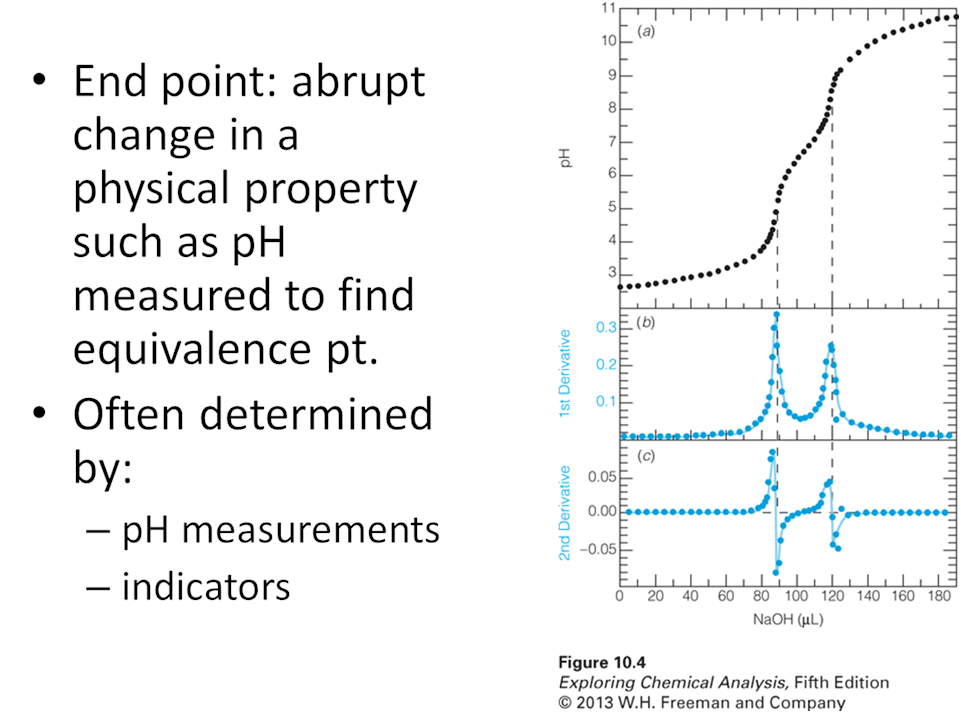
    Fig10.4.png

    • Think back to when you took general chemistry and you learned how to perform an acid base titration. As a group write out the basic steps to determine the concentration of a weak acid from a titration with a weak base.

     

     

     

     

     

     

    STOP

     

    Generic Approach to Quantitative Analysis

    1.  
    2.  
    3.  
    4.  

    *Our known must really be known, how do we get that?

     
    • In the previous unit we learned about primary standards for use in calibration curves, standard addition curves, and internals standards. Can your group think of a way to use a standard to standardize your titrant?

     

     

     

    STOP

    Standards and Standardization. The key to being able to relate titrant to analyte is in knowing the concentration of the titrant. Done via primary standard. i.e. Na2CO3(s) can be made pure enough that weighing it out gives an exact mass that when made in solution only gives random error. Does not decompose and must be stable when dried. Titrant is standardized via a primary standard and then the known concentration of the titrant can be used in the future.

    • Standard oxalate was made by dissolving 3.514g of Na2C2O4 (FM 134.00) in 1.000 L of 1 M H2SO4. A 25.00 mL aliquot required 24.44 mL of KMnO4 for titration, and a blank required 0.03 mL of KMnO4. Find the molarity of KMnO4 so it can then be used as a titrant.

    \[\ce{5C2O4^2- + 2MnO4- +16H+ → 10CO2 + 2Mn^2+ + 8H2O}\nonumber\]

     

     

     

     

     

     

     

     

     

     

    STOP

    • A 20.00 mL aliquot of unknown oxalic acid solution required 17.81 mL of 0.01131 M KMnO4 solution to reach the purple end point. A blank titration of 10 mL of similar solution containing no oxalic acid required 0.02 mL to exhibit detectable color. What is the concentration of the oxalic acid unknown?

       

       

       

       

       

       

       

    STOP

     

    Solubility Product and Common Ion Effect

    Reading: Chapter 6 (sections 4-6), Exploring Chemical Analysis 5th ed., D. Harris

    • As a group decided how would you explain solubility product (Ksp).

     

     

     

    STOP

    • What is the concentration of Pb2+ in a saturated PbI2 solution if you know the Ksp=7.9×10‑9?

     

     

     

     

     

     

     

    • What is the concentration of I- in the same PbI2 solution?

     

     

     

     

     

     

     

     

     

    STOP

    • Which way would the previous reaction for the solubility of PbI2 go if you tried to dissolve PbI2 in a solution NaI? Why?

     

     

     

     

     

     

    STOP

    • Instead of just dissolving PbI2(s) in H2O let's dissolve it in the presence of 0.0300 M NaI(s) which dissociates completely. What is the concentration of Pb2+ in solution? *note sometimes we need to make approximations to neglect small contributors to the value so we can solve eqn.















       

    STOP

    • If I add Ag+ to a mixture of I- and Cl- which should precipitate first? ie. Which salt favors solid formation?

    \[\ce{Ag+ + I- → AgI_{(s)}} \hspace{20px}  \mathrm{K_{sp}=8.3⨯10^{-17}}\nonumber\]

    \[\ce{Ag+ + Cl- → AgCl_{(s)}} \hspace{20px}  \mathrm{K_{sp}=1.8⨯10^{-10}}\nonumber\]

     

     

     

     

     

     

     

     

    STOP

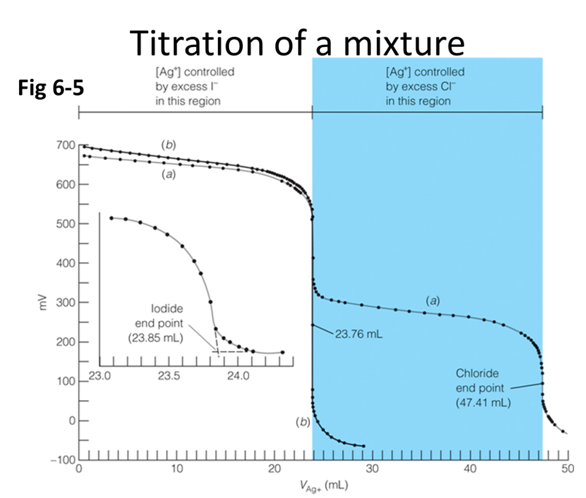
    Fig6-5.png

    • In the titration curve above (Fig 6-5) 40.00 mL of unknown solution containing I- and Cl- were titrated with 0.0915 M Ag+. What is the concentration of both ions?

     

     

     

     

     

     

     

     

     

     

     

     

     

    STOP

    volhard_titration.png

    Contributors and Attributions

    This page titled Quantitative Analysis: Nuts and Bolts is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Contributor via source content that was edited to the style and standards of the LibreTexts platform.