Measurements and Uncertainty
- Page ID
- 279684
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Pre-Class Assignment
Many times in chemistry, we are trying to determine a physical or chemical property through a measurement. Yet each measurement we make could have some error associated with it. Read section 1.6 in your textbook (also posted to Moodle) and read about standard deviation using the following website. Then answer your assigned question as we prepare to learn about different types of errors and uncertainties in scientific measurements.
https://www.mathsisfun.com/data/standard-deviation.html
If your last name starts with A-L, answer question 1 and bring it in to class on Monday.
If your last name starts with M-Z, answer question 2 and bring it to class on Monday.
Question 1:
- What is the definition of the term accuracy?
- What is a systematic error? Give an example.
- How is an average calculated? What mathematical equation is used? Define all the terms that contribute to the average.
Question 2:
- What is the definition of the term precision?
- What is a random error? Give an example.
- How is the sample standard deviation calculated? What mathematical equation is used? Define all the terms that contribute to the standard deviation.
In-Class Assignment*
Groups will work together to answer all questions.
- Discuss the terms accuracy and precision from the reading. Define both terms using your own words.
Accuracy –
Precision –
- Based on your definitions, determine what a dartboard would look like if the dart thrower is both accurate and precise, accurate but not precise, precise but not accurate, and neither accurate nor precise. Assume you have five darts for each board. Draw all four boards on your whiteboard.




- All measurements have some sort of error associated with them. The type of error and the magnitude of that error is extremely important to understanding and trusting the result of your measurement or calculation. Discuss the terms systematic and random error. What is the difference between them? On your white board, give an example of each not given in the text.
Systematic error –
Random error –
Which type of error most affects accuracy in a measurement? Why?
Which type of error most affects precision in a measurement? Why?
- As you should now understand, not all measurements can be done with infinite precision. All measurements will have some error or uncertainty in them. We can represent that error in different ways. First let’s quantitate accuracy and precision using the average and standard deviation. What equations are used to describe average and standard deviation? Make sure your entire group understands each term.
- Bias is a term used to describe the difference between the average calculated result and the true value. Write out a mathematical expression for bias.
- The following graduated cylinders were used to measure the volume of a known quantity of water.* Imagine that each has been filled with 3.420 mL of water. Cylinders A and C have 5 mL capacities and graduation marks at 0.1 mL. Cylinders B and D have 25 mL capacities and graduations at each 1 mL; they are readable to the tenths place. A student makes five independent readings of the volume in each cylinder and tabulates the data. For each flask, calculate the average, range (largest minus smallest), standard deviation, bias (average compared to the true value), and percent error. Each group will be assigned a single cylinder. Report the values for your cylinder on your white board.
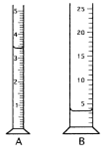
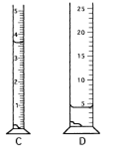
|
Cylinder |
Measured Value (mL) |
Mean (mL) |
Precision |
Accuracy |
||
|---|---|---|---|---|---|---|
|
Range (mL) |
Std Dev (mL) |
Bias (mL) |
Percent Error |
|||
|
A |
3.42 3.43 3.41 3.44 3.41 |
|
|
|
|
|
|
B |
3.5 3.3 3.4 3.3 3.4 |
|
|
|
|
|
|
C |
3.67 3.65 3.64 3.68 3.65 |
|
|
|
|
|
|
D |
4.2 4.1 4.3 4.3 4.1 |
|
|
|
|
|
Focusing on the bias and percent error for each cylinder, comment on which would be better for comparisons.
- Based on your calculations from question 6, determine which graduated cylinder is accurate and precise, accurate but imprecise, precise but inaccurate, and neither accurate nor precise.
Put this table on your whiteboard.Accurate & Precise
Accurate
Precise
Neither
- Using the figures in question 6 and your conclusions from question 7, suggest a reason why two of the flasks are inaccurate and two are imprecise. Write these ideas on your white board.
To finish on your own after class:
- Fill in the blanks in the following sentences using the words and phrases from the word bank.*
Set one:
A measurement is precise if it is in agreement with _____________________________________________. In other words, it is ___________. The extent of the agreement can be expressed as the ______________ ____________________________________________.
A measurement is accurate if it is in agreement with ___________________________________________. In other words, it is ___________. The extent of the agreement can be expressed as the ______________ ____________________________________________.
Set one word bank:
repeated measurements by the same procedure correct range or standard deviation
reproducible the true value absolute error or percent error
Set two:
An error in measurement can occur ________________. In which case, it is classified as _______________ and it causes poor precision. The effect of the error can be reduced by _____________________________ ____________________________________________.
An error in measurement can occur ________________. In which case, it is classified as _______________ and it causes poor accuracy. The effect of the error can be reduced by _____________________________ ____________________________________________.
Set two word bank:
Repeating the measurement and averaging the results systematic random
inconsistently running a standard and applying a correction factor consistently
Contributors and Attributions
- Amber Hupp, College of the Holy Cross (ahupp@holycross.edu)
- *Important note: This worksheet was inspired by “Precision and accuracy in measurements. A tale of four graduated cylinders”. All data and many concepts are derived from: R.S.Treptow. J. Chem. Ed. 75 (1998) 992-995.


