Electrochemistry: Basic Concepts
- Page ID
- 283158
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A REDOX Example
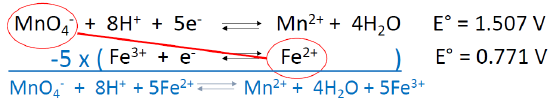
- One would predict a spontaneous reaction between….
- What is the coefficient in front of Fe2+ in the balanced reaction?
- What is E° for the total reaction?
ΔG, E and K Example
Eo for the following reaction (as written) is 0.736 volts. Calculate ΔG and K for the reaction.
\[\ce{MnO4- + 8H+ + 5Fe^2+ ⇌ Mn^2+ + 4H2O + 5Fe^3+}\nonumber\]
Calculating Potential of a Cell (Nernst equations)
Calculate the potential for the following cell:
\[\mathrm{Pt \mid Sn^{2+}(0.400\: M),\: Sn^{4+}(0.500\: M) \mid\mid NO_3^-(0.100\: M),\: H^+(pH=2.00),\: HNO_2(0.400\: M) \mid Pt}\nonumber\]
Potentiometry – Cells (line notation with REF)
Calculate the cell potential of the following cell:
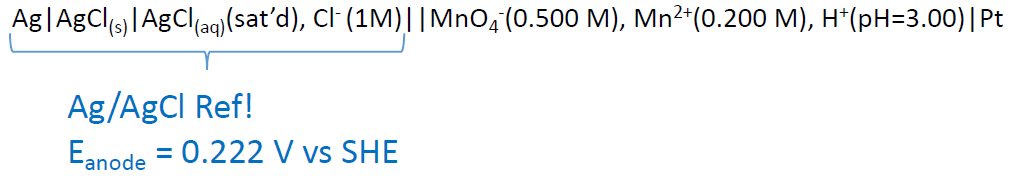
Bringing in Ksp
Think about the previous problem…
Calculate the cell potential of the following cell:
\[\mathrm{Ag \mid AgCl_{(s)} \mid AgCl_{(aq)}(sat’d),\: Cl^- (1.00\: M) \mid\mid \textrm{reduction half cell} \mid Pt}\nonumber\]
Couldn’t one use the Ag+ + e- ⇌ Ag(s) half cell at Eo = 0.799?
“Adding” Reactions
When you “add” chemical reactions, you multiply the K values and/or add the E values.
Given the following Eo values:
\[\ce{Ag+ + e- ⇌ Ag_{(s)}} \textrm{ (0.799 V vs SHE) and}\nonumber\]
\[\ce{AgCl_{(s)} + e- ⇌ Ag_{(s)} + Cl-} \textrm{ (0.222 V vs SHE)}\nonumber\]
Calculate the Ksp for AgCl.
“Mixing” Problems
30.00 mL of 0.120 F NaNO3 is mixed with 20.00 mL of 0.150 F SnCl2 and the solutions is buffered at pH=2.00. (NOTE: no gas or solid is observed)
- Calculate Eo and K for the spontaneous reaction that will occur.
- Calculate the solution potential of the resulting solution.
Potentiometry Problems (mixing, then measuring)
Calculate the cell potential, as measured at a Pt/SCE electrode pair, for a solution prepared by mixing 30.00 mL of 0.120 F NaNO3 and 20.00 mL of 0.150 F SnCl2. The solution is buffered at pH=2.00. (except for SCE, this is the same problem as the previous exercise)
Potentiometry Problems, II (mixing, then measuring, EP)
Calculate the cell potential, as measured at a Pt/SCE electrode pair, for a solution prepared by mixing 25.00 mL of 0.120 F NaNO3 and 20.00 mL of 0.150 F SnCl2. The solution is buffered at pH=2.00.
KEY: Reactant conc’ns are “Not really zero, just really small….AND in a defined ratio” …as indicated by coefficients in balanced eqn!
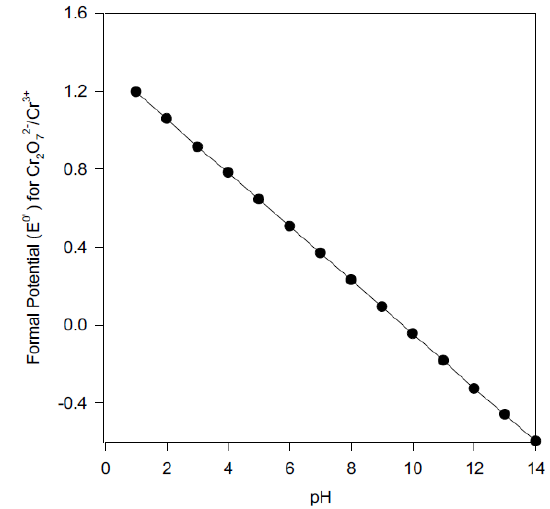
Formal Potential (Eo’)
Derive an equation for the pH-dependent formal potential for the dichromate/ chromium III half reaction, and calculate the Eo’ at pH 7.00.
\[\ce{Cr2O7^2- + 14H+ + 6e- ⇌ 2Cr^3+ + 7H2O} \hspace{30px} \mathrm{E^o} = \textrm{1.33 V vs SHE}\nonumber\]
\[E^{0'}_{Cr_2O_7^{2-}/Cr^{3+}} = E^0_{Cr_2O_7^{2-}/Cr^{3+}} - \dfrac{0.0591}{6} \log\left(\dfrac{1}{[H^+]^{14}}\right)\nonumber\]
\[E^{0'}_{Cr_2O_7^{2-}/Cr^{3+}} = E^0_{Cr_2O_7^{2-}/Cr^{3+}} - \dfrac{0.0591(14)}{6} pH\nonumber\]
\[\mathrm{E^{o’}}\textrm{ at pH 7.00 = 0.365 V vs SHE}\nonumber\]
Redox Titration
Consider the titration of 50.00 mL of 0.100 M Cr2O72- with 0.300 M Fe2+ as monitored with a Pt/SCE electrode pair...calculate the measured cell potential and construct the expected titration plot. The pH is maintained at 0.00.
\[\ce{Cr2O7^2- + 14H+ + 6e- ⇌ 2Cr^3+ + 7H2O} \hspace{30px} \mathrm{E^o} = \textrm{1.33 V vs SHE}\nonumber\]
\[\ce{Fe^3+ + e- ⇌ Fe^2+} \hspace{30px} \mathrm{E^o} = \textrm{0.771 V vs SHE}\nonumber\]
Contributors and Attributions
- Timothy Strein, Bucknell University (strein@bucknell.edu)
- Sourced from the Analytical Sciences Digital Library