Concentration Calibration Procedures

Accurately knowing the amount, in terms of concentration, of a particular substance (analyte)  is important in fundamental research and also in many applied fields of study such as medicine, environmental studies, and the food industry.

In medicine, many drug dosages are effective within a narrow concentration range.  If too little is administered, the benefits of the drug will not be obtained.  However, if too much is administered in a particular time frame, overdose or toxicity can occur.  Therefore, many patients must have their blood tested on a regular basis to determine the amount of such drugs in their system.   Also, many common analytes such a metals are required by the human body at low levels, but are toxic to the cells at high levels.

In environmental studies, it is important to ensure that levels of environmental contaminants are monitored.  In 2010 the BP Oil spill devastated the wildlife on the Gulf Coast of Mexico in the United States.  It was one of the worst environmental accidents in the history of the United States.  Years and vast amounts of money was required to clean up the spill.  The Gulf waters have since been deemed safe to use; however, four years later, scientists still monitor the concentration of oil contaminants to ensure safety of Gulf water for patron use.

The previous examples provide important reasons for knowing the concentration of a particular analyte in a sample (biological fluid, water, food etc.).  The substance that we want to know the amount of in a sample is called the analyte.  In order to determine the concentration of a particular analyte in a sample we must perform a procedure called “concentration calibration”. This module discusses the three most common types of concentration calibration procedures.

Analytes themselves cannot be measured directly; however, specific properties of the analyte can.  Many analysis techniques that we will talk about at the end of the semester provide a response to a solution containing some concentration of an analyte.  Two common ways to get a response for an analyte is to measured light absorbance or an electrochemical property. However, the absorption or electrochemical response of an analyte can rarely be used alone to determine the concentration in the sample.  For example, the absorption or electrochemical measurement might be slightly different from one day to the next for the exact same sample due to a variety of uncontrollable variables including background noise from the instrument.

• If an instrument response to the same concentration of an analyte varies from day-to-day, can you devise a general procedure to determine the concentration of an analyte in a solution despite this issue? Report to your professor when done before moving on.

 

 

 

 

 

General steps of a concentration calibration: 

Finding suitable standard solutions

A primary standard analyte solution is a solution that contains a known amount of the analyte called the standard.  The standard may be a pure analyte, a solution containing the analyte, or a solution containing the analyte along with other solutes; in either case, the analyte concentration is accurately known.  The solution may be a solid, liquid, or gas phase solution and the standard analyte may exist in either of these three phases as well.  Standards are referred to as Standard Reference Materials (SRM) because they have been tested by The National Institute of Standards and Technology (NIST). This agency ensures the analyte concentration in many types of samples is accurate.  The picture below is a SRM for Gulf of Mexico Crude Oil, which may be used to test for crude oil contaminants, for example to monitor the safety of the gulf waters after the BP oil spill.

Figure taken from:  http://www.nist.gov/publication-portal.cfm?defaultSearch=false&researchfield=245

• What are common characteristics of a primary standard such as the one shown above?

 

 

 

• Do you think that standards are available for all analytes? Why or why not? Elaborate.

 

 

 

---

STOP

Calibration Curve

To help you understand the ideas of calibration curve and standard addition curves we are going to use a cartoon example, but it translates directly into any chemistry scenario where the dependent variable (y) varies linearly with the independent variable (x).

• Imagine that you have 5 containers as shown below and assume that each ball gives an instrument response of 3. Determine the instrument response for each of the containers, plot the instrument response (dependent variable) vs. number of balls (independent variable), and determine using the graph how many balls are present if the instrument response is 26. Be sure to label the graph.

---

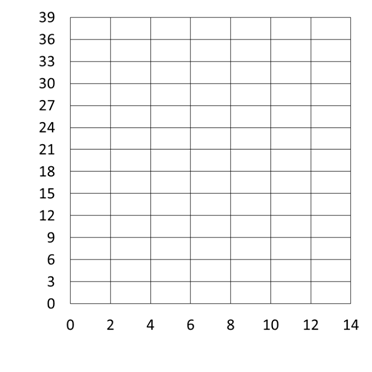
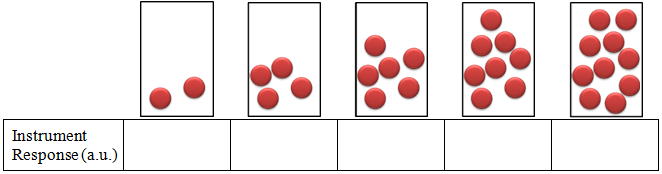
STOP

As a group work through this real lab problem on using calibration. This is very similar to what you will do in Quantitative Analysis Laboratory and EXAMS for this class.

• Using a Calibration Curve

  Below is a calibration curve for the determination of vitamin C (ascorbic acid [AA]) via voltammetry. This allows us to plot the current as a function of concentration. Four standards have been made (4.00, 8.00, 12.00, and 16.00 μM) and run to create the calibration curve. Then three fruit juice samples with an unknown amount of vitamin C are run and the current is recorded (Fruit Juice).

• The table above is readily available from Excel whenever you create a calibration curve and use the LINEST function. You will learn how to create this table in CHEM 316, but you need to know how to use the data in it for this class. Therefore, label all variables in the tables above so you will be able to readily use them. *Note: standard deviation is always given as “s” with a subscript denoting what it is the standard deviation of.
• What is the average concentration of vitamin C in the 3 samples?

 

 

 

 

 

 

 

• Draw a horizontal line on the plot from the average measured current for the diluted sample to the calibration curve. Then draw a vertical line from the curve to the appropriate concentration on the x-axis.  This provides a graphical check of your math.  Does your graphical check confirm your math?

 

• Determine the uncertainty, s_x, of the sample concentration.

 

 

 

 

 

 

 

 

 

 

 

• Calculate the confidence interval and write the complete confidence interval (e.g. XX±YY μM) with the correct number of significant figures.

 

 

 

 

 

 

 

 

 

 

• If the detection limit is 0.20 µM, what is the quantitation limit? (come back to after we learn LOD, LOQ, and sensitivity)

 

 

 

 

 

 

• The y-intercept is non-zero. What could this be indicative of?        

 

 

---

STOP

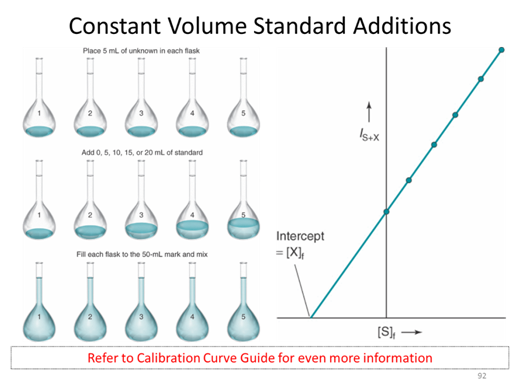
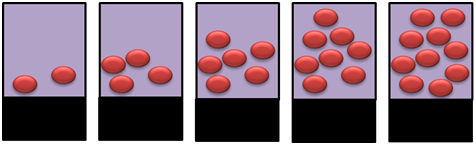
Assuming that we have to take the measurement in the presence of the purple solution which is very hard to make or may not have a standard solution. We start with some unknown amount of balls that I am covering up with a black box so you can’t see them. We put 2 additional balls in and collect an instrument response. We repeat this spiking procedure 4 more times. This is referred to as a constant volume standard addition, for which the initial concentration is given by the absolute value of the x-intercept. (The derivation of this fact is in section 5-3 if you are interested)

• Given the standard addition graph below determine the initial concentration of the solution that has been spiked.

---

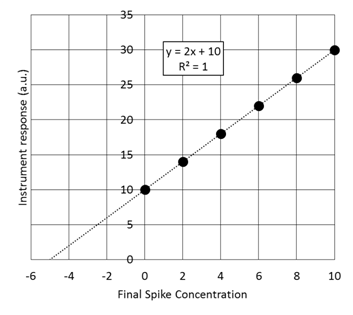
STOP

• Using a Standard Addition Curve

  Brilliant Blue G (BBG) dye was recently discovered as promising dye to analyze the extent of spinal cord injury.  In this experiment, standard addition was used to minimize the matrix effect in determining concentration of BBG in a sample of spinal fluid.  

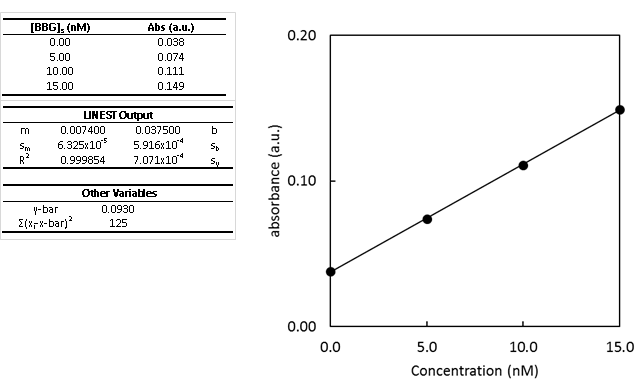
• Determine the concentration of BBG in the unspiked sample using the standard addition curve.

 

 

 

 

 

• Second, determine the uncertainty in the concentration of BBG.

 

 

 

 

 

 

 

• Calculate and write the complete confidence interval with the correct number of significant figures.

 

 

 

 

 

 

 

• The y-intercept is non-zero. What could this be indicative of?        

 

 

---

STOP

Internal Standard Activity

Suppose you wanted to measure the quercetin concentration in a plant food such as Prunus serotina.  Before performing the measurement, you would first need to remove quercetin from the plant sample because the plant itself will not be compatible with the measurement technique.  For example, most measurement techniques require the sample in liquid form.  A likely procedure for removing the quercetin from the plant is to use an extraction process.  A sample of the plant might be mixed with a suitable solvent in a blender, homogenized, and filtered.  One concern in this process is whether all of the quercetin has been extracted from the plant.  If a lesser amount is extracted, the concentration of quercetin in Prunus serotina will be underestimated using an external standard curve.

• Can your group think of a way to determine the extraction efficiency of an analyte such as quercetin?

 

 

 

 

---

STOP

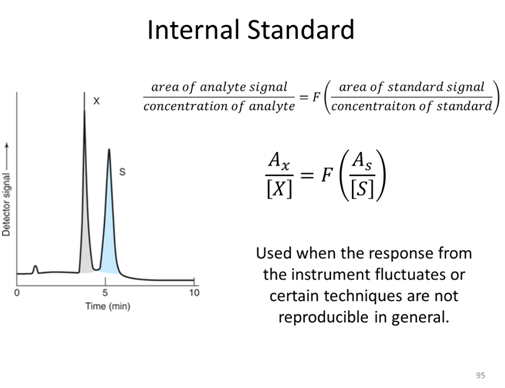
• A standard solution containing 75 ppm of quercetin and 60 ppm of internal standard kaempferol gave peak areas of 300 and 200, respectively. A plant sample is spiked such that the extract to be analyzed should have 60 ppm of kaempferol.  Analysis of the sample gives a peak area for the kaempferol of 163.  The quercetin peak in the same extract has an area of 407.  What is the concentration of quercetin in the extract?

 

 

 

 

 

 

 

 

---

STOP

• What are the LOD, LOQ, and sensitivity for the calibration curve made for [Cu²⁺] via AA?

  \(
  \:\:\textrm{LOD Data (a.u.)}\\
  \begin{array}{|c|c|}
  \hline
  &\textrm{AA} \\
  \hline
  1& 0.025 \\
  \hline
  2& 0.026 \\
  \hline
  3& 0.025 \\
  \hline
  4& 0.026 \\
  \hline
  5& 0.026 \\
  \hline
  6& 0.03 \\
  \hline
  7& 0.027 \\
  \hline
  8& 0.028 \\
  \hline
  9& 0.027 \\
  \hline
  10& 0.028 \\
  \hline
  \textrm{std dev} & 0.00154  \\
  \hline
  \textrm{m} & 5170.55 \\
  \hline
  \end{array}
  \nonumber\)

   

   

   

   

---

STOP

From a previous exam:

• Trace elements, such as Sr, in teeth of archeological specimens provide anthropologists with clues about diet and diseases of ancient people. Atomic absorption spectroscopy measurements were collected to determine the amount of Sr in a tooth specimen. Use the data to answer the following questions a-f.

  

   

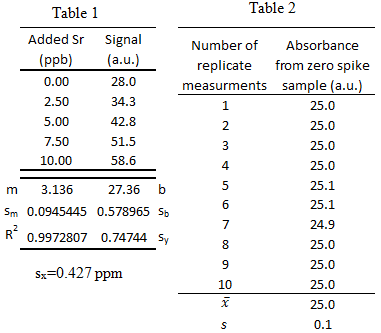
  1. What is the 95% confidence interval for unknown Sr concentration? Write the confidence interval in this form: XX ± YY.

      

      

      

      

      

      

      

      

      

      

      

      

      

      

      

      

      

      

  2. What is the limit of detection for the calibration curve?

      

      

      

      

      

  3. What is the limit of quantification for the calibration curve?

      

      

      

      

      

  4. What is the sensitivity for the calibration curve?

      

      

      

      

      

      

  5. Could the concentration 0.2 ppb be measured via this method? \(\dfrac{yes\: or\: no}{circle\: one}\)

      

      

      

  6. Could the concentration 0.2 ppb be quantified via this method? \(\dfrac{yes\: or\: no}{circle\: one}\)

      

      

      

      

      

      

From a previous exam:

• Standard solutions of a blue protein were made and their absorbance was measured at 508 nm using UV-vis spectroscopy. The standard calibration curve and LINEST output are shown below in Table 1. A unknown sample was also measured and the 3 replicate measurements are listed in Table 1. The measurements of the lowest concentration sample, 1.6670 µg/mL, was measured 10 times and the resulting absorbance values are listed in Table 2.

  

  

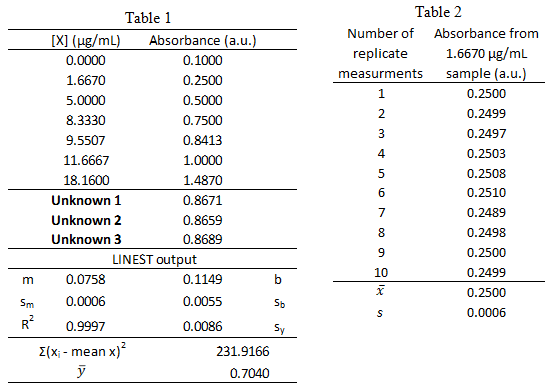
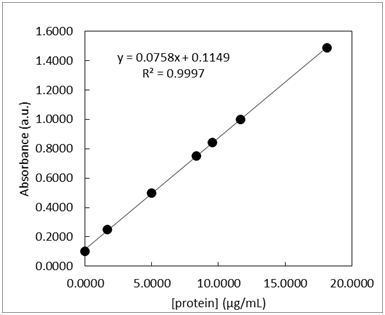
  1. What is the 95% confidence interval for unknown protein concentration? Write the confidence interval in this form: XX ± YY.

      

      

      

      

      

      

      

      

      

      

      

      

      

      

      

      

  2. What is the limit of detection for the calibration curve?

      

      

      

      

      

  3. What is the limit of quantification for the calibration curve?

      

      

      

      

      

  4. What is the sensitivity for the calibration curve?

      

      

      

      

      

      

  5. Could the concentration 0.06 µg/mL be measured via this method? \(\dfrac{yes\: or\: no}{circle\: one}\)

      

  6. Could the concentration 0.06 µg/mL be quantified via this method? \(\dfrac{yes\: or\: no}{circle\: one}\)

      

      

Contributors and Attributions

• Allyson Fry-Petit, California State University Fullerton ([e-mail])
• NOTE:  This exercise is a modification of a module on the Active Learning site on Concentration Calibration written by Sandra Barnes.  http://community.asdlib.org/activelearningmaterials/files/2014/08/CC_In_Class_Modular_Unit2.pdf
  • Available on LibreTexts: In-Class Modular Unit
• Sourced from the Analytical Sciences Digital Library