Buret Calibration and Stardardization of NaOH Solution
- Page ID
- 281938
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Exercise Learning Objectives:
- Use basic output from an analytical tool (buret) to calibrate that tool.
- Use data to perform error analysis (identify the presence of random and/or systematic errors).
- Standardize a sodium hydroxide (NaOH) solution using titration of potassium hydrogen phthalate (KHP) using a calibrated buret.
- Report the determined concentration of the standardized NaOH solution.
- Communicate (oral and written) scientific concepts related to calibration and standardization.
In Class Exercise:
- Work in groups of 3 or 4 students.
- Develop a consensus for the questions in the exercise
- Where appropriate use Excel
Introduction: Class A burets are a common type of volumetric glassware that is used to deliver variable volumes of a solution. Burets are commonly used when performing titration reactions. A 50 mL class A buret has a tolerance of ±0.05 mL. Like most tools used to make quantitative determinations in the laboratory volumetric glassware can and should be calibrated to improve accuracy.

Accurately determining the amount of an analyte (unknown), in terms of concentration, is largely dependent on the quality (accuracy) to which standards are known and the quality of the tools (sensitivity and calibration accuracy) used to make the determination. This is critical in successfully conducting both fundamental and applied research as well as quality control measures in various industries.
Acid and base titrations are an extremely common approach to using stoichiometry to quantitatively measure the concentration of an analyte in solution. In this exercise you will be using the data provided to determine the concentration of a NaOH solution that is prepared by dissolving NaOH(s) in DI water. While properly calibrated analytical balances are one of the most accurate laboratory tools, accurately determining the mass of NaOH(s) is difficult. This is because NaOH is very hygroscopic. This means that NaOH will absorb water in the atmosphere, and as a result when you measure the mass of NaOH on a balance you are likely measuring NaOH plus some amount of water. Therefore, the mass of NaOH should be treated as an approximate value. Titration of a standard acid, such as KHP, with the NaOH solution can be used to accurately determine the concentration of the NaOH solution.
KHP is commonly used as a primary standard because it is a solid at room temperature, is stable in air, and is not hygroscopic, which makes it possible to accurately determine the mass of KHP using a balance. A primary standard is characterized as a reagent of higher purity and is typically a stable solid such that a measurement of mass accurately representative of the number of moles of the standard. Secondary standards are those that are prepared in reference to a primary standard (i.e. standardized against a primary standard). In the context of this exercise the NaOH solution is a secondary standard that is standardized against the primary standard (KHP) using laboratory titration.
Question 1: Explain in layman terms what is meant by the term “concentration” and give examples of common units for concentration in analytical measurements?
Question 2: Why might mass measurements using an analytical balance to measure about 25 g of water be considered more accurate than a volume measurements of 25 mL with volumetric glassware, such as burets or transfer pipets? (Hint: consider significant figures, physicochemical properties, physical process, etc.)
Part 1: Buret Calibration
Using the data provided (Table 1) to calibrate the 50 mL volumetric pipet that will be used to standardize the NaOH solution. In carrying out this exercise it is recommended that you utilize Microsoft Excel to manipulate data and perform the necessary mathematical operations. The measurements for the calibration data include reading the volume level of DI water in a buret as successive volumes of DI water are delivered into a flask. After each volume of DI water is delivered the flask the mass of the flask + water is rapidly measured using an analytical balance. This process is performed three times. The temperature in the lab at the time of the measurements was 23.0 °C. Note that the first measurement for each trial is the starting volume of water in the buret and prior to delivering any water to the flask.
Table 1: Buret Calibration Data (Buret volume and mass of water dispensed)
|
Calibration Trial |
Buret Reading (mL) |
Mass of Flask + Contents (g) |
|---|---|---|
|
Trial 1 |
0.01 |
50.2205 |
|
5.02 |
55.1947 |
|
|
9.99 |
60.1388 |
|
|
15.01 |
65.1599 |
|
|
19.96 |
70.0444 |
|
|
25.03 |
75.1065 |
|
|
30.05 |
80.0997 |
|
|
34.97 |
85.0292 |
|
|
40.02 |
90.0117 |
|
|
45.01 |
95.0031 |
|
|
50.00 |
99.9614 |
|
|
Trial 2 |
0.02 |
50.2225 |
|
5.00 |
55.1847 |
|
|
10.01 |
60.1488 |
|
|
15.01 |
65.1499 |
|
|
20.05 |
70.1044 |
|
|
25.02 |
75.0865 |
|
|
29.99 |
80.0511 |
|
|
34.99 |
85.0169 |
|
|
40.02 |
90.0003 |
|
|
45.00 |
94.9733 |
|
|
49.98 |
99.9209 |
|
|
Trial 3 |
0.00 |
50.4185 |
|
5.01 |
55.3577 |
|
|
9.98 |
60.3397 |
|
|
15.03 |
65.4102 |
|
|
19.99 |
70.2814 |
|
|
25.01 |
75.3165 |
|
|
30.01 |
80.2807 |
|
|
34.99 |
85.2182 |
|
|
40.03 |
90.2217 |
|
|
44.99 |
95.1931 |
|
|
49.98 |
100.1114 |
Use the data in Table 1 to calibrate the buret. Please describe the outcome of the calibration process (consider using text, a table and/or a figure to describe the outcome).
Question 3: Does the class A buret accurately deliver the measured volume? Explain.
Question 4: What evidence exists for the presence of random and systematic errors?
Question 5: If random or systematic errors are observed, hypothesize a source of the error(s).
Part 2: Standardization of NaOH solution
You will be using the buret calibrated in Part 1 of this exercise and the data provided in Table 2 report the standardized concentration of the NaOH solution. The NaOH solution is standardized using the titration of a primary standard of KHP (Figure 2). The titration reaction of KHP with NaOH is as follows:
\[\ce{C8H5KO4 (aq) + NaOH (aq) → H2O + C8H4NaKO4 (aq)}\nonumber\]
The NaOH solution is prepared by measuring out about 25 g of NaOH(s), which is then transferred to a 1 L volumetric flask. The NaOH is dissolved by filling the volumetric flask to the mark. To perform each titration approximately 2.5 g of KHP is transferred into a 100 mL beaker. The KHP is then dissolved with about 25 mL of water. The KHP is then titrated by delivering the NaOH solution from the calibrated buret from part 1. This process is repeated 5 times.
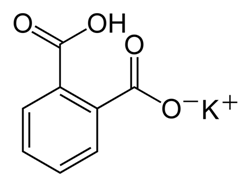
C8H5KO4
204.22 g mol-1
pKa = 5.4
water solubility 80 g L-1 (20 °C)
Figure 2: Chemical structure for potassium hydrogen phthalate (KHP) and properties.
The progress of the titration reaction is monitored using a color indicator (phenolphthalein). As the titration reaction progresses the endpoint is marked by the solution going from clear to pink.
Table 2: NaOH standardization by titration of KHP
|
Trial |
Mass of KHP (g) |
Starting Buret Reading (mL) |
Final Buret Reading (mL) |
|---|---|---|---|
|
1 |
2.5191 |
0.04 |
19.26 |
|
2 |
2.4875 |
0.02 |
19.21 |
|
3 |
2.5503 |
0.03 |
19.48 |
|
4 |
2.5106 |
1.14 |
23.93 |
|
5 |
2.4611 |
0.25 |
19.32 |
Use the buret calibrated in Part 1 and the data in Table 2 to standardize the NaOH solution described in Part 2. Report the concentration in molarity (M). As with Part 1, it is recommended that you utilize Microsoft Excel to manipulate data and perform the necessary mathematical operations.
Question 6: How should the concentration of NaOH be reported?
Question 7: How was the conclusion(s) in Part 1 used while completing Part 2 of this exercise?
Summary: Prepare a single PowerPoint slide or Word document that summarizes the key results or points from this exercise. Email this document to the instructor.
Contributors and Attributions
- Chad Kinney, University of Colorado Pueblo (chad.kinney@csupueblo.edu)
- Sourced from the Analytical Sciences Digital Library


