Skip to main content
Chemistry LibreTexts

Acids and Bases

  1. Last updated
  2. Save as PDF
  • Page ID
    282034

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Acids and Bases

    Acid and Bases: Arrhenius. The Arrhenius equation defines acid as a compound that increases the concentration of H+ (or H3O+) in solution, and base as a compound that increases the concentration of OH- in solution. As a group write out generic expressions for acid dissociation and base hydrolysis. How do the expressions change if you denote the acid or base as strong or weak?

    Reading and Homework: separated by type below

    • As a group write out generic expressions for acid dissociation and base hydrolysis including the appropriate equilibrium expression




     

    • How do the expressions change if you denote the acid or base as strong or weak?





     

    STOP

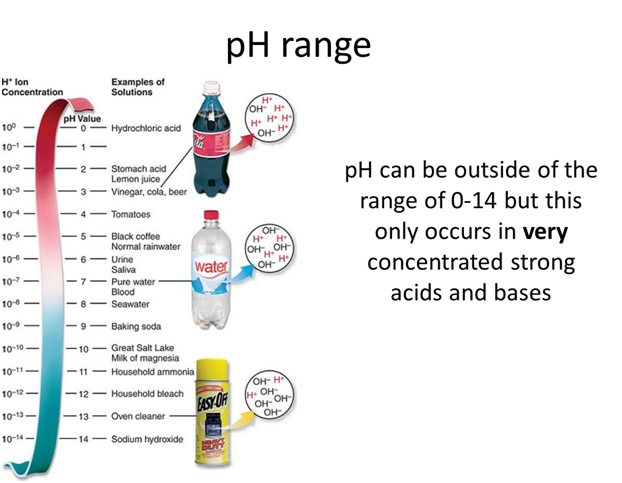
    pH_Range.png

    SigFigs_LogAntilog.png

     

    Strong Acid or Strong Base

    Reading: Chapter 8 (sections 1-4), Chapter 10 (sections 1, 4), Exploring Chemical Analysis 5th ed., D. Harris 

    • What is the pH of concentrated (11.6 M) hydrochloric acid?







     

    STOP

    Through the rest of this unit we are going to use an online tool to help us remember what we know about acid-base titrations and expand our understanding to more complex systems. It is important that one person in the group brings a laptop or tablet capable of running the website.


     

    • Click on Investigation 1
    • Uncheck the [titrant] = initial [analyte] box under Titrant before proceeding
    • Monitor the change in the titration curve of a strong acid with a strong base and explain the effect of changing the following variables with the slider on the curve. Remember that you should only change one variable at a time.
      • Initial analyte concentration (M)

         

         

         

      • Titrant concentration (M)

         

         

      • Initial volume (mL)

         

         

         

    • Which indicators are suitable for the titration of a strong acid with a strong base?

     

     

     

    • How does the titration curve change if the analyte is changed from a strong acid to a strong base?

     

     

    STOP

    • Use the website first to determine the answer to the following questions and then prove them mathematically. Be sure to write the relevant rxn for each of the 3 regions of the titration curve.
      • How many mL of 0.05 M NaOH are needed to reach equivalence of the titration of 20 mL 0.01 M HCl?

        \(\begin{array}{c}
        &\textrm{website}\\
        &\begin{array}{|c|}
        \hline
        \hspace{150px} \\ \\ \\
        \hline\end{array}
        \end{array}\)




         

      • What pH would be observed at the equivalence point and what is the rxn occurring in the flask?

        \(\begin{array}{c}
        &\textrm{website}\\
        &\begin{array}{|c|}
        \hline
        \hspace{150px} \\ \\ \\
        \hline\end{array}
        \end{array}\)





         

      • What is the pH at 2 mL of NaOH added and what is the rxn occurring in the flask?

        \(\begin{array}{c}
        &\textrm{website}\\
        &\begin{array}{|c|}
        \hline
        \hspace{150px} \\ \\ \\
        \hline\end{array}
        \end{array}\)







         

      • What is the pH at 6 mL of NaOH added and what is the rxn occurring in the flask?

        \(\begin{array}{c}
        &\textrm{website}\\
        &\begin{array}{|c|}
        \hline
        \hspace{150px} \\ \\ \\
        \hline\end{array}
        \end{array}\)






         

        STOP

      • Draw the titration curve

        Axes_TitrationCurve.png

      • Which indicator would be suitable for this titration?

     

     

     

     

    • What is the pH of water (by calc. not memory)?

    \[H_2O ⇌ H^+ + OH^- \hspace{20px} K_a=1.0 × 10^{-14}\nonumber\]

     

     

     


    STOP

    Titration_StrongBase,StrongAcid.png

     

    Weak Acid or Weak Base

    Reading: Chapter 8 (sections 5-7)
    Homework: Chapter 8: 10, 11, 14-16, 19-23, 25, 28, 30, 32, 33

    WeakAcids,Bases.png

    Quadratic formula. Do I always have to do the quadratic formula? NO if it follows the 1% rule then the x in the denominator can be neglected. K/F < 10^-4

    • What is the pH of 0.100 M formic acid solution, Ka= 1.80×10-4?













     

    STOP

    Relation of K_a, K_b, and K_w: K_a × K_b = K_w. You should know how to derive this relationship (next slide). Important because if we know that K_a or K_b of an acid or a base we can determine the K_b of K_a of its conjugate respectively. Appendix B (and most tables of dissociation constants) only list K_a.

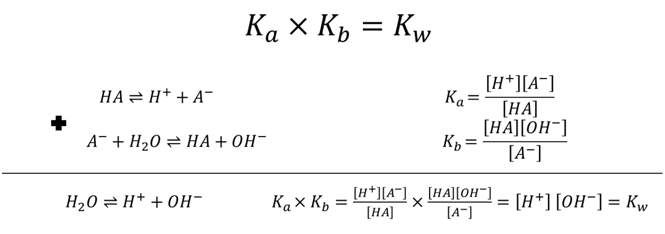
    Ka,Kb,Kw_Equations.png

    • NH4+ Ka=5.7×10-10 what is Kb for NH3?

     

     

     

     

    STOP

    pKa,pKb.png

     
    • Which acid is stronger dichloroacetic, Ka=8.00x10-2, or chloroacetic, Ka=1.36x10-3? How does Ka and pKa relate to strength?








     

    STOP

    • Find pKa of a weak acid 0.063 M hydrobenzene with a pH=5.60.

     

     

     

     

     

    Prediction of acidic and basic solutions formed by salts. Salts: solid that results from an acid-base neutralization reaction. Most are strong electrolytes and therefore dissociate completely in H2O. Metal ions with a charge ≥ 2 are acidic. Is the aqueous solution of the salt CH3NH3Cl acidic or basic?

    STOP

     

    Buffers

    Reading: Chapter 9 (sections 1-6), Exploring Chemical Analysis 5th ed., D. Harris

    • How would your group define a buffer?

     

     

     

     

     

    Buffer,LeChatelier.png

    Henderson-HasselbalchEqn.png

    Henderson-HasselbalchEqnDerivation.png

    • What ratio of [A-]/[HA] will create an acetic acid (Ka=1.75x10-5) buffer with a pH=5.0?

     




     

    STOP

    • A buffer is made with 2.402 g of acetic acid (Ka=1.75x10-5, FW: 60.05) and 3.247 g of its conjugate, acetate ion (FW: 59.04), in 5L H2O what is the pH?

     

     

     

     

     

     

     

    STOP

    Using a buffer: application of L.C.P.

    • What happens if a strong acid is added to a buffer soln.?

    \[HA ⇌ H^+ + A^- \nonumber\]

     

     

    • What happens if a strong base is added to a buffer soln.?

    \[B + H_2O ⇌ BH^+ + OH^- \nonumber\]

     

    STOP

     
    • Add 1.276 g HCl (FW: 36.4609) to the acetic acid buffer example on the previous page and calculate the new pH. (*hint: ice table)
















     

    • How does this relate to the pH before strong acid is added? What would the pH be if 1.276 g HCl was added to water without the buffer solution?




















     

    STOP

     

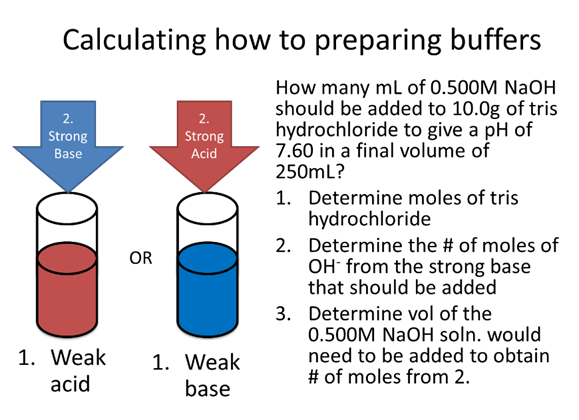
    BufferPreparationCalculation.png

    • How many mL of 0.500M NaOH should be added to 10.0g of tris hydrochloride (pKa=8.07, FW=157.60g/mol) to give a pH of 7.60 in a final volume of 250mL?

     

     

     

     

     

     

     

     

     

     

    STOP

     

    Buffers_PreparingInRealLife.png

    BufferCapacity.png

     

    Acid-BaseIndicators.png

    • Yellow @ pH=3.7
      • What is [B-]:[Y] when first yellow?

     

     

     

     

    • Blue @ pH=5.7
      • What is [B-]:[Y] when first blue?

     

     

     

     

    STOP

     

    Quantitative Analysis: Titrations

    The rest of this unit will focus on the use of titrations to determine the quantity of an analyte. That will include acid-base with one equivalence point (monoprotic), acid-base with several equivalence points (polyprotic), and EDTA titrations. Along the way we will also consider how equilibrium can be affected by the presence of different ions.

    Learning Objectives

    By the end of this students should be able to:

    1. Perform calculations to determine the quantity of an analyte via the following types of titrations: acid-base monoprotic and polyprotic and EDTA.
    2. Determine the fractional composition of a system and be able to display that understanding in a principle species diagram.
    3. Explain the concept of activities and the effect on equilibrium.
    4. Calculate the activity of ions.

    Monoprotic Titrations

    Reading: Chapter 10 (sections 1-5), Exploring Chemical Analysis 5th ed., D. Harris 

    We are going to combine everything we reviewed in the last few chapters on acids, bases, and buffers to determine the quantity of an unknown acid or base. For some of you this chapter will seem so familiar the tendency will be to not practice. However, we are going to do polyprotic titration in the next chapter so you need to be rock solid on this material! So practice practice practice!

    We are going to generate a titration curve for each type of titration

    • Weak acid with strong base
    • Weak base with strong acid

    Titration of Weak Acid w/ Strong Base (pg 210-213)






     

     
    • Click on Investigation 2
    • Uncheck the [titrant] = initial [analyte] box under Titrant before proceeding
    • Monitor the change in the titration curve of a weak acid with a strong base and explain the effect of changing the following variables with the slider on the curve. Remember that you should only change one variable at a time.
      • ­pKa

         

         

      • Initial analyte concentration (M)

         

         

      • Titrant concentration (M)

         

         

      • Initial volume (mL)

     

     

    • Why was pKa considered a variable for a weak-strong titration but not a strong-strong?

     

     

    • How does the titration curve change if the analyte is changed from a weak acid to a weak base?

     

     

    STOP

     
    • Use the website first to determine the answer to the following questions and then prove them mathematically. Be sure to write the relevant rxn for each of the 3 regions of the titration curve.
    • Generate the titration curve for the titration of 25.00 mL of 0.20 M HF (Ka = 6.6×10-4) with 0.15 M NaOH.
      • How many mL of 0.15 M NaOH are needed to reach equivalence of the titration of 25.00 mL 0.20 M HF?

        \(\begin{array}{c}
        &\textrm{website}\\
        &\begin{array}{|c|}
        \hline
        \hspace{150px} \\ \\ \\
        \hline\end{array}
        \end{array}\)




         

      • What pH would be observed at the equivalence point and what is the rxn occurring in the flask?

        \(\begin{array}{c}
        &\textrm{website}\\
        &\begin{array}{|c|}
        \hline
        \hspace{150px} \\ \\ \\
        \hline\end{array}
        \end{array}\)





         

      • What is the pH at 20 mL of NaOH added and what is the rxn occurring in the flask?

        \(\begin{array}{c}
        &\textrm{website}\\
        &\begin{array}{|c|}
        \hline
        \hspace{150px} \\ \\ \\
        \hline\end{array}
        \end{array}\)






         

      • What is the pH at 60 mL of NaOH added and what is the rxn occurring in the flask?

        \(\begin{array}{c}
        &\textrm{website}\\
        &\begin{array}{|c|}
        \hline
        \hspace{150px} \\ \\ \\
        \hline\end{array}
        \end{array}\)

         



         

        STOP

      • Draw the titration curve

        Axes_TitrationCurve.png

      • Which indicator would be suitable for this titration?

         

         

         

        STOP

         

      • Fill out table
    Region pH defining species and type of rxn
    Before any titrant  
    Before eq. pt.  
    At eq. pt.  
    After eq. pt.  

     

     

    Titration of Weak Base w/ Strong Acid (pg 214-215)

    Axes_Va,pH.png

    Region pH defining species and type of rxn
    Before any titrant  
    Before eq. pt.  
    At eq. pt.  
    After eq. pt.  
    • Based on what we just learned can we predict the 4 regions and draw the curve?

     

     

     

     

    Polyprotic Titrations

    TitrationReferenceSheet.png

    Reading: Chapter 11 (sections 1,2, 4), Exploring Chemical Analysis 5th ed., D. Harris 

     

    Many molecules have many proton donor or acceptor sites (such as amino acids and thus proteins!). Therefore, we need to know how they react, what can we know about concentrations when we know pH, and what would a titration look like. Often in biochemistry you will not look at the full titration only a piece, but you can’t understand a part unless you understand the whole!

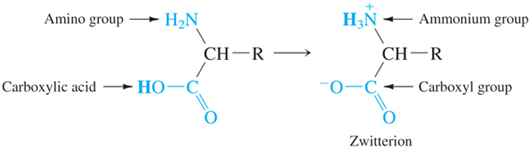
    AminoAcid.png

    • There is a pKa for both groups on the molecule (amino acid in this case), which group is going to act more like and acid and therefore which should have a lower pKa?

     

     


    STOP

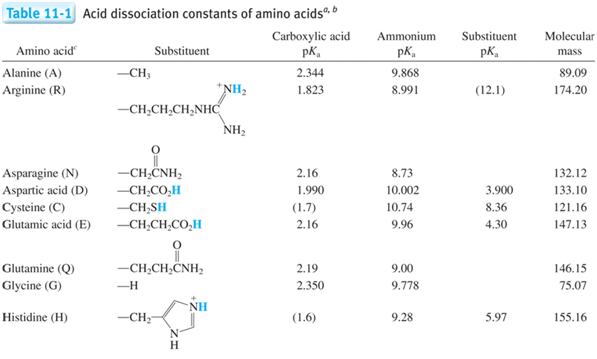
    Table11-1_AcidDissociationConstants_AminoAcids.png

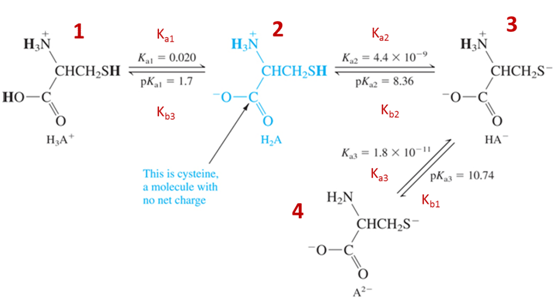
    Cysteine_EquilibriumConstants.png

    • Which species above is the strongest acid? \(\underset{\textrm{circle one}}{\underline{\textrm{1, 2, 3, or 4}}}\)
    • Which species above is the strongest base? \(\underset{\textrm{circle one}}{\underline{\textrm{1, 2, 3, or 4}}}\)
    • What is the corresponding relation when you have multiple Ka and Kb such as polyprotic systems?
      • Derive the relation between K1a, K3b, and Kw.
















     

    STOP

     
    • Click on Investigation 3
    • Uncheck the [titrant] = initial [analyte] box under Titrant before proceeding
    • Monitor the change in the titration curve of a diprotic weak acid with a strong base and explain the effect of changing the following variables with the slider on the curve. Remember that you should only change one variable at a time.
      • ­pKa1

         

         

      • ­pKa2

         

         

      • Initial analyte concentration (M)

         

         

      • Titrant concentration (M)

         

         

      • Initial volume (mL)

         

         

    • Why do we need to consider more than 1 pKa for a polyprotic titration?

     

     

     

     

    • How does the titration curve change if the analyte is changed from a weak acid to a weak base?

     


     

    STOP

     
    • Draw a generic titration curve H2A+ with a strong base

      Regions where we will identify the pH and the volume:

      1. Initial
      2. @ all equivalence points
      3. @ ½ each equivalence point
      4. Any point in a buffer region
      5. After the last equivalence point

    Axes_pH,Vb.png

    • Use the website first to determine the answer to the following questions and then prove them mathematically. Be sure to write the relevant rxn for each region of the titration curve.
    • Generate the titration curve for the titration of 10 mL of 0.200 M alanine (pKa1 = 2.344, pKa2 = 9.868) with 0.100 M NaOH by walking through the following questions.
      • What is the pH before any base is added?

        Initially (before any base added) the pH defining rxn is

        \(\begin{array}{c}
        &\textrm{website}\\
        &\begin{array}{|c|}
        \hline
        \hspace{150px} \\ \\ \\
        \hline\end{array}
        \end{array}\)



         

      • What is the volume to the 1st and 2nd equivalence?

        \(\begin{array}{c}
        &\textrm{website}\\
        &\begin{array}{|c|}
        \hline
        \hspace{150px} \\ \\ \\
        \hline\end{array}
        \end{array}\)





         

      • What is the pH at the first equivalence point?

        At the first equivalence point the pH is defined by \(\underset{fill\: in}{\underline{\hspace{200px}}}\) and the approximation \(\underset{fill\: in}{\underline{\hspace{200px}}}\).

        \(\begin{array}{c}
        &\textrm{website}\\
        &\begin{array}{|c|}
        \hline
        \hspace{150px} \\ \\ \\
        \hline\end{array}
        \end{array}\)



         

      • What is the pH at the last equivalence point?

        At the last equivalence points the pH is defined by  \(\underset{fill\: in}{\underline{\hspace{200px}}}\).

        \(\begin{array}{c}
        &\textrm{website}\\
        &\begin{array}{|c|}
        \hline
        \hspace{150px} \\ \\ \\
        \hline\end{array}
        \end{array}\)

         

         

         

         

         

         

      • What is the pH at halfway to each equivalence point?

        ½ way to each equivalence point the pH is defined by \(\underset{fill\: in}{\underline{\hspace{200px}}}\) and the approximation \(\underset{fill\: in}{\underline{\hspace{200px}}}\).

        \(\begin{array}{c}
        &\textrm{website}\\
        &\begin{array}{|c|}
        \hline
        \hspace{150px} \\ \\ \\
        \hline\end{array}
        \end{array}\)







         

         
      • What is the pH after 23.00 mL of NaOH has been added?

        Any point before an equivalence point the pH is defined by \(\underset{fill\: in}{\underline{\hspace{200px}}}\).

        \(\begin{array}{c}
        &\textrm{website}\\
        &\begin{array}{|c|}
        \hline
        \hspace{150px} \\ \\ \\
        \hline\end{array}
        \end{array}\)













         

         
      • What is the pH after \(\underset{insert\: volume}{\underline{\hspace{100px} mL}}\) of NaOH has been added?

        Any point after the last equivalence point the pH is defined by \(\underset{fill\: in}{\underline{\hspace{200px}}}\).

        \(\begin{array}{c}
        &\textrm{website}\\
        &\begin{array}{|c|}
        \hline
        \hspace{150px} \\ \\ \\
        \hline\end{array}
        \end{array}\)












         

     

    From last semester’s second exam; worth 25% of the exam

    Titration of 12.00 mL of fumaric acid requires 26.00 mL of 0.0300 M potassium hydroxide to reach the first equivalence point. 

    Disregard significant figures and give all pH and volumes values with 2 decimal places.

    Fill in the empty boxes on the titration curve and show the work in the space provided on this page and the next with the corresponding letter. A value provided without sufficient work shown will receive no credit.

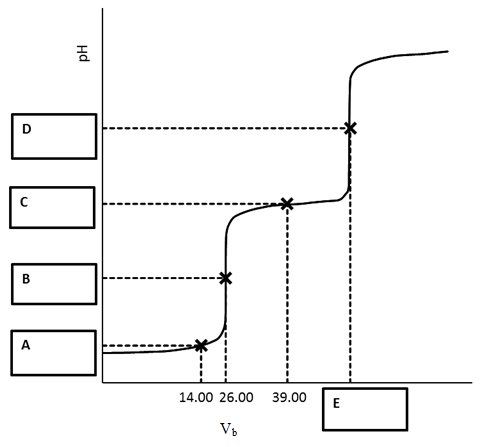
    TitrationCurve.png

    1. pH at A







     

    1. pH at B







     

    1. pH at C








     

    1. pH at D
















     

    1. Volume at E

     

     

     

     

    Contributors and Attributions

    This page titled Acids and Bases is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Contributor via source content that was edited to the style and standards of the LibreTexts platform.