Problem 3
- Page ID
- 302053
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Calculate the pH of a solution that is 0.147 M in pyridine and 0.189 M in pyridinium chloride.
The first step in any equilibrium problem is to determine a reaction that describes the system. This system has appreciable quantities of both pyridine (Py) and pyridinium chloride. The structure of pyridine is shown below and is a base.
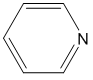
As a base it could undergo the following reaction (note that this is the Kb reaction).
\[\ce{Py + H2O \leftrightarrow PyH+ + OH-}\nonumber\]
The structure of pyridinium chloride is shown below. It is important to realize that when added to water, the pyridinium and chloride ions will separate from each other such that the ions will be solvated by water (the pyridinium ion will have the negative oxygen atoms directed toward it, the chloride ion will have the positive hydrogen atoms of the water directed toward it)
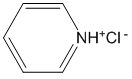
We can write potential reactions for both the pyridinium and chloride ions reacting with water as follows.
\[\ce{PyH+ + H2O \leftrightarrow Py + H3O+}\nonumber\]
Note that this is the Ka reaction for pyridinium. Looking in the table of values shows a pKa of 5.22. This means that pyridinium is a weak acid.
\[\ce{Cl- + H2O \leftrightarrow HCl + OH-}\nonumber\]
Note that this is the Kb reaction for chloride. Chloride is the conjugate base of hydrochloric acid. Looking up hydrochloric acid in the table shows that hydrochloric acid is a strong acid, meaning that it reacts essentially 100% in water to produce Cl– and H3O+. Because of this, the reaction above of chloride with water to produce HCl and hydroxide ion will not occur and can be ignored.
At this point it seems we have two reactions (the Kb reaction for pyridine producing pyridinium and hydroxide being one, the Ka reaction for pyridinium producing pyridine and hydronium being the other) that describe the system. As a test, let's do the calculation using both possible reactions.
Using pyridine acting as a base (pKb = 8.78, Kb = 1.66\(\times\)10-9):
\[\begin{align}
& &&\ce{Py}\hspace{25px} +\hspace{25px} \ce{H2O} \hspace{25px}\leftrightarrow &&\ce{PyH+} \hspace{25px} + &&\ce{OH-} \nonumber \\
&\ce{Initial} &&0.147 &&0.189 &&0 \nonumber \\
&\ce{Equilibrium} &&0.147 - \ce{x} &&0.189+\ce{x} && \ce{x} \nonumber \\
&\ce{Approximation} &&0.147 &&0.189 &&\ce{x} \nonumber
\end{align}\nonumber\]
Note that the initial amount of hydroxide, which is set at 0, assumes that the amount that will be produced is significant compared to 10-7 M. Also, the approximations can be attempted since the value of Kb is small.
The approximations can now be plugged into the Kb expression and x evaluated.
\[\mathrm{K_b = \dfrac{[PyH^+][OH^-]}{[Py]} = \dfrac{(0.189)(x)}{0.147} = 1.66\times10^{-9}}\nonumber\]
\[\mathrm{x = [OH^-] = 1.29\times10^{-9}}\nonumber\]
However, we must first check the approximation before calculating the pH.
\[\dfrac{1.29\times10^{-9}}{0.147} \times 100 = 8.77 \times 10^{-7}\% \hspace{60px} \dfrac{1.29\times10^{-9}}{0.189} \times 100 = 6.83 \times 10^{-7}\%\nonumber\]
These approximations are both valid. However, if you consider that we ignored the initial amount of hydroxide present from the autoprotolysis of water (10-7 M), this would seem to be in error because of the low level of hydroxide (1.29\(\times\)10-9 M). For the moment, let’s just move ahead assuming it was okay to ignore the autoprotolysis of water, and more will be said later about the appropriateness of this decision. The concentration of hydronium ion and pH can be calculated.
\[\mathrm{[H_3O^+] = 7.75 \times 10^{-6} \qquad pH = 5.11}\nonumber\]
Using pyridinium acting as an acid (pKa = 5.22, Ka = 6.03\(\times\)10-6):
\[\begin{align}
& &&\ce{PyH+}\hspace{25px} +\hspace{25px} \ce{H2O} \hspace{25px}\leftrightarrow &&\ce{Py} \hspace{25px} + &&\ce{H3O+} \nonumber \\
&\ce{Initial} &&0.189 &&0.147 &&0 \nonumber \\
&\ce{Equilibrium} &&0.189 - \ce{x} &&0.147+\ce{x} && \ce{x} \nonumber \\
&\ce{Approximation} &&0.189 &&0.147 &&\ce{x} \nonumber
\end{align}\nonumber\]
The approximations can now be plugged into the Ka expression and x evaluated.
\[\mathrm{K_a = \dfrac{[Py][H_3O^+]}{[PyH^+]} = \dfrac{(0.147)(x)}{0.189} = 6.03 \times 10^{-6}}\nonumber\]
\[\mathrm{x = [H_3O^+] = 7.75\times10^{-6}}\nonumber\]
However, we must first check the approximation before calculating the pH.
\[\dfrac{7.75\times10^{-6}}{0.147} \times 100 = 0.00527\% \hspace{60px} \dfrac{7.75\times10^{-6}}{0.189} \times 100 = 0.00410\%\nonumber\]
In this case, we can also examine whether it was appropriate to ignore the hydronium ion concentration from the autoprotolysis of water.
\[\dfrac{1.0\times10^{-7}}{7.75\times10^{-6}} \times 100 = 1.29\%\nonumber\]
In this case (unlike with the pyridine acting as a base), ignoring the autoprotolysis of water is appropriate.
Since all of the approximations are valid, we can use the hydronium ion concentration to calculate the pH.
\[\mathrm{[H_3O^+] = 7.75 \times 10^{-6} \qquad pH = 5.11}\nonumber\]
What is important to realize that we get the same pH (5.11) using either the Ka or Kb equation. These two answers are reassuring but also problematic. The reassuring part is that a solution can only have one pH. If either of the two reactions can be used to describe the system, then both ought to give the same answer for the pH. But one reaction has pyridine acting as a base, another pyridinium acting as an acid. Which one is actually correct? The way to assess that is to examine the relative values of Ka for the conjugate acid and Kb for the conjugate base. In this case, the Ka for the acid is about 1,000 times larger than the Kb for the base. Because of that, a small amount of the acid would dissociate to the base. And note, we did get a pH that was acidic for the answer in each case. But it really does not matter since the amount of change is so small that it can be ignored.
However, there is something very important to realize about this system. A solution with appreciable concentrations of both members of a conjugate pair is known as a buffer. Buffers are solutions that resist changes in pH. This resistance is created by having both members of the conjugate pair.
If acid is added, the base component of the conjugate pair reacts to form the conjugate acid.
If base is added, the acid component of the conjugate pair reacts to form the conjugate base.
As long as the concentration of the buffer components are not excessively dilute (on the order of 10-6 M or lower), a buffer controls the pH of the system and in buffer solutions we can always ignore the initial concentration of hydronium or hydroxide ion from the autoprotolysis of water. A convenient way to calculate the pH of a buffer is to use what is known as the Henderson-Hasselbalch equation. This equation can be derived from the Ka expression.
Ka expression:
\[\mathrm{K_a = \dfrac{[Py][H_3O^+]}{[PyH^+]}}\nonumber\]
Take the negative logarithm of both sides:
\[\mathrm{-\log K_a = -\log \left(\dfrac{[Py][H_3O^+]}{[PyH^+]} \right )}\nonumber\]
Rearrange the right hand side using the properties of logs:
\[\mathrm{-\log K_a = -\log \left(\dfrac{[Py]}{[PyH^+]} \right ) - \log[H_3O^+]}\nonumber\]
Remember that:
\[\mathrm{-\log(K_a) = pK_a}\nonumber\]
\[\mathrm{-\log[H_3O^+] = pH}\nonumber\]
Substituting these in gives:
\[\mathrm{pK_a = -\log \left(\dfrac{[Py]}{[PyH^+]} \right ) + pH}\nonumber\]
Rearranging gives the final form of the Henderson-Hasselbalch equation:
\[\mathrm{pH = pK_a + \log \left(\dfrac{[Py]}{[PyH^+]} \right )}\nonumber\]
If we substitute in the values for this problem (and note, with a buffer we will be able to ignore any redistribution of the appreciable amount of the two species), we get:
\[\mathrm{pH = pK_a + \log \left(\dfrac{[Py]}{[PyH^+]} \right ) = 5.22 + \log\left(\dfrac{0.147}{0.189} \right ) = 5.11}\nonumber\]
This is the same answer we got using either the Ka or Kb expressions.
We can also write two generalized forms of the Henderson-Hasselbalch equation for the two generalized types of weak acid/weak base buffer solutions (the generalized formulas for a weak acid, HA and BH+).
\[\ce{HA + H2O \leftrightarrow A- + H3O+}\nonumber\]
\[\mathrm{pH = pK_a + \log\left(\dfrac{[A^-]}{[HA]} \right )}\nonumber\]
\[\ce{BH+ + H2O \leftrightarrow B + H3O+}\nonumber\]
\[\mathrm{pH = pK_a + \log\left(\dfrac{[B]}{[BH^+]} \right )}\nonumber\]
Earlier we said that a buffer is effective at controlling the pH because the acid form of the conjugate pair can neutralize bases and the base form can neutralize acids. Examining the Henderson-Hasselbalch equation also allows us to appreciate from a quantitative sense how buffers are able to control the pH of a solution. If you look at this equation, you notice that the pH is expressed as a constant (pKa) that then varies by the log of a ratio. One thing to note about log terms is that they change rather slowly. Someone who offers you the log of a million dollars is not being very generous with their money. It takes a very large change in the ratio of the two concentrations to make a large difference in the log term. This large change will only occur when one of the two components of the buffer gets used up by virtue of the acid or base that is being added.
Contributors and Attributions
- Thomas Wenzel, Bates College (twenzel@bates.edu)
- Sourced from the Analytical Sciences Digital Library


