Tanabe-Sugano Diagrams

Introduction

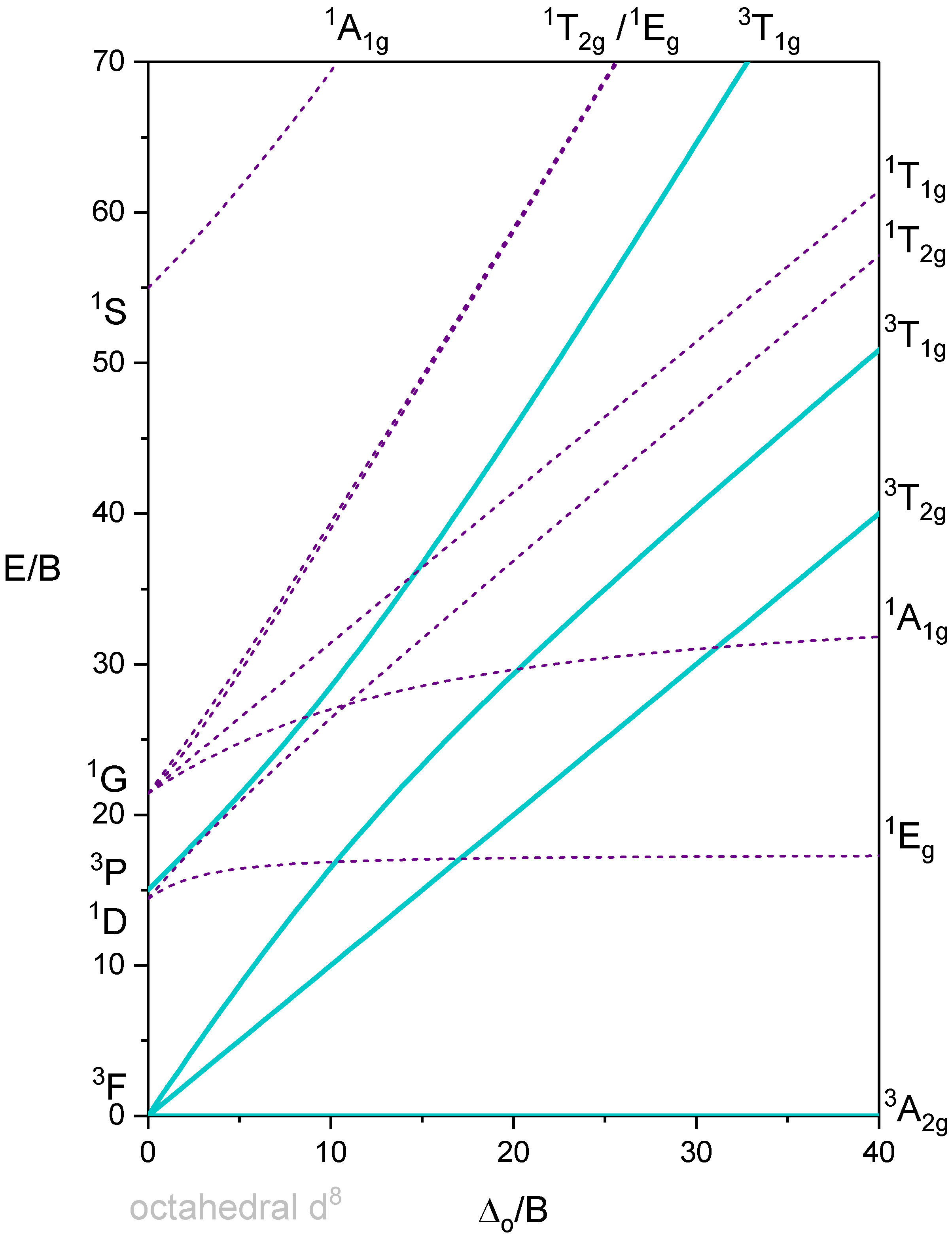
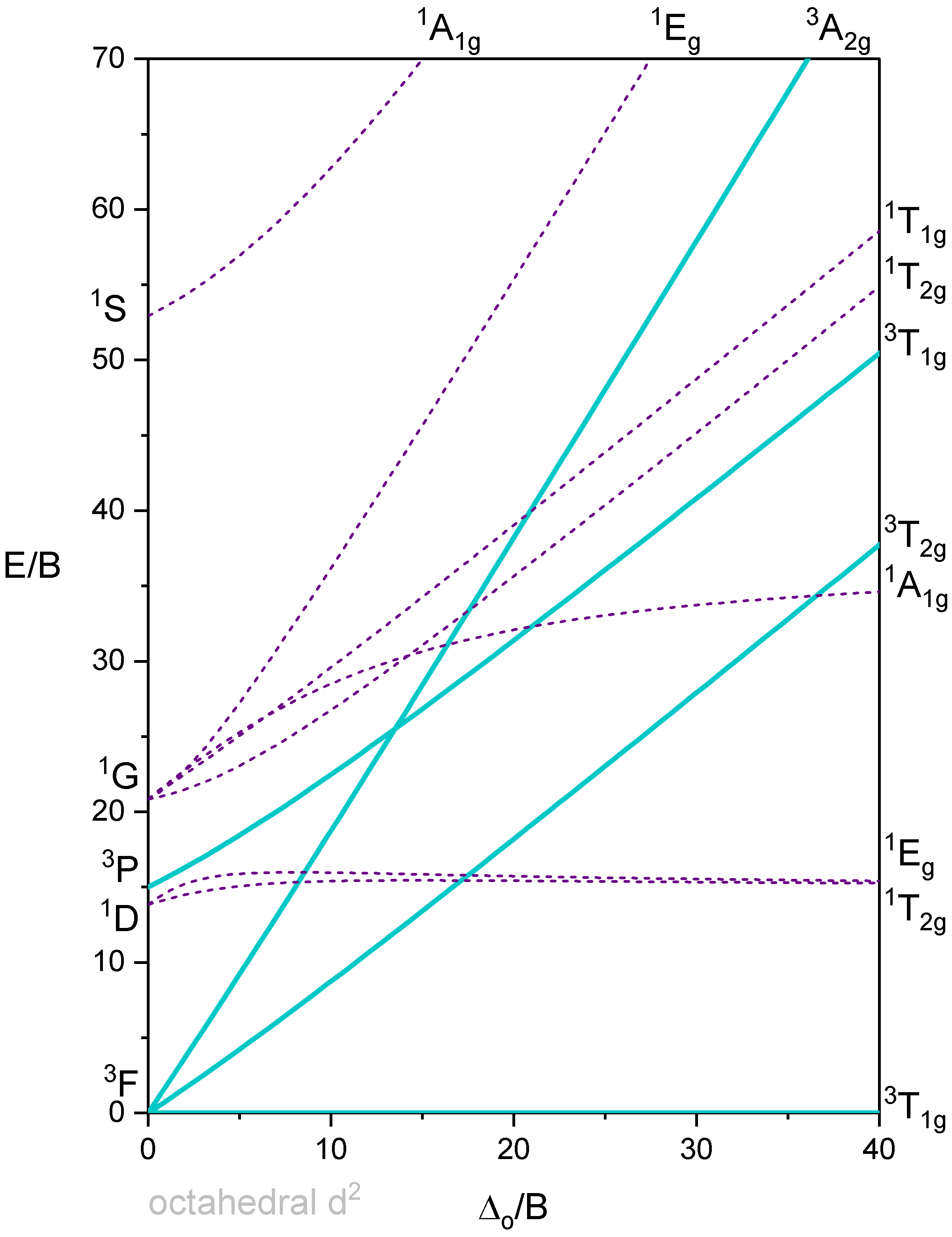
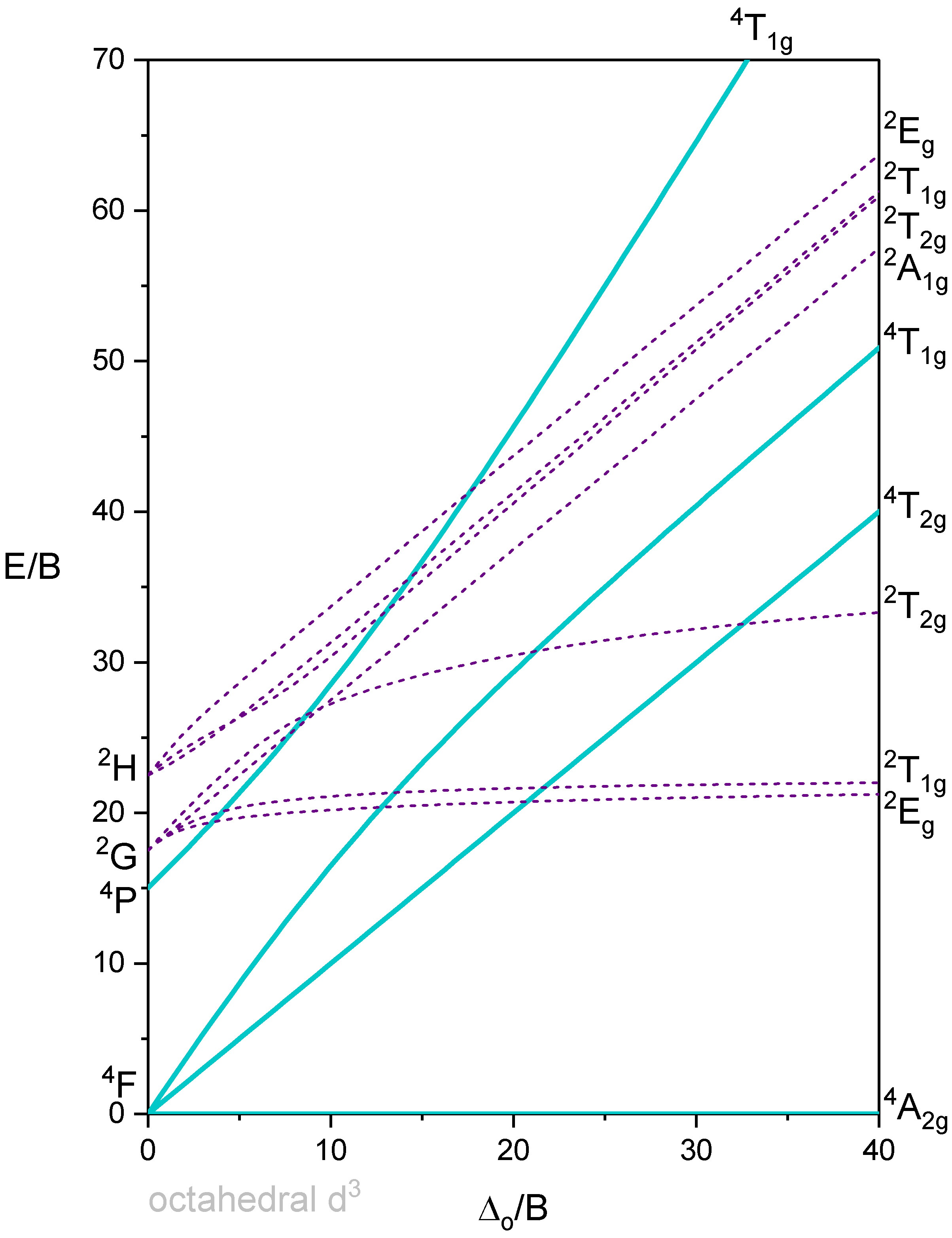
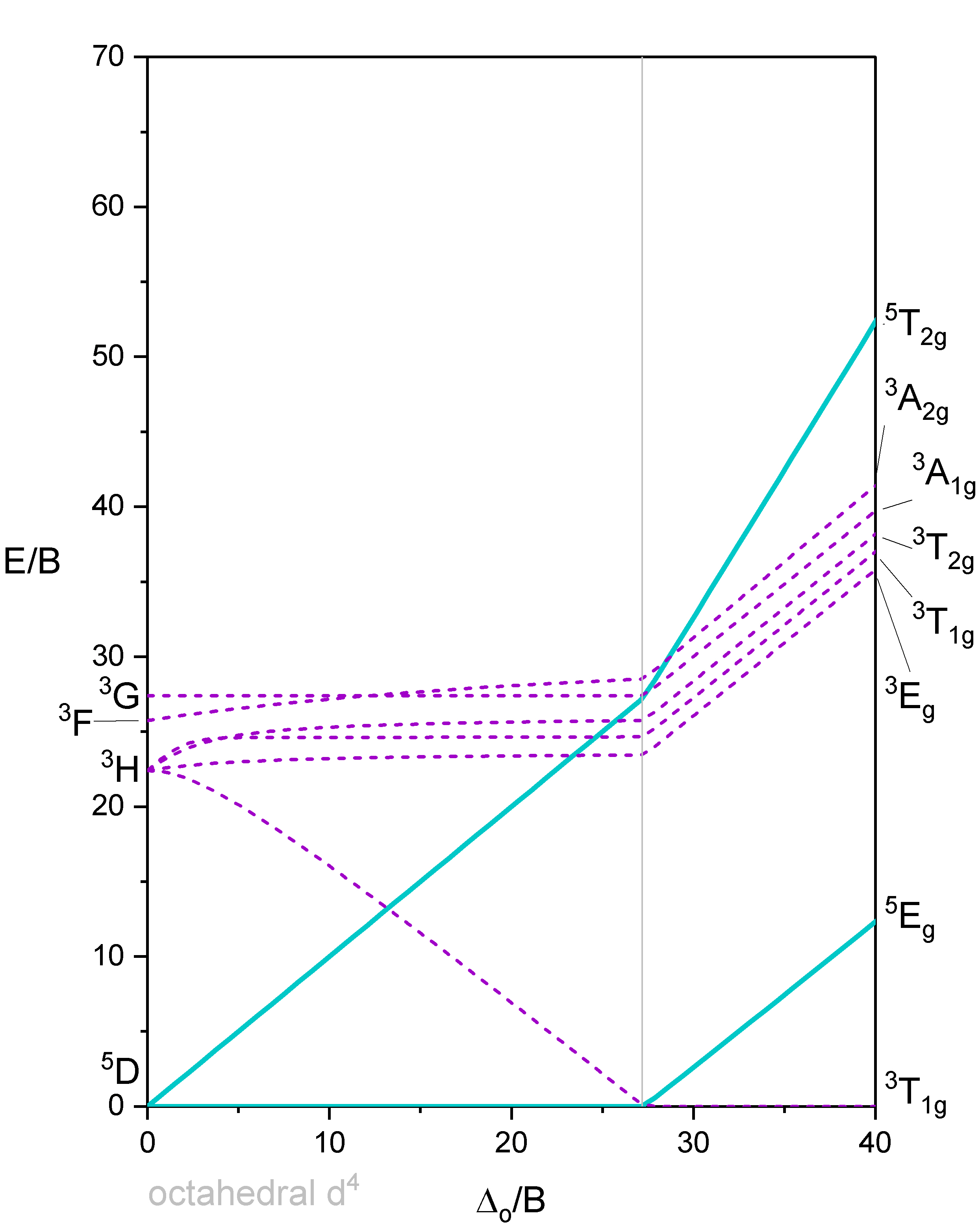
Tanabe-Sugano Diagrams are a form of correlation diagrams. These diagrams show relative energies of terms (eg. electronic microstates) by plotting the splitting energy and the field strength in terms of the Racah Parameter, B (plotted as \(\frac{E}{B}\) vs \(\frac{\Delta}{B}\)). The Racah parameter accounts for \(d\)-electron-electron repulsions that affect the energies of the terms (and thus the transition energy). These diagrams are useful for interpreting electronic spectra. Specifically, the diagrams can be used to qualitatively predict the number of spin-allowed and spin-forbidden transitions, the relative intensities of these transitions, and their relative energies. The diagrams can also be used to estimate the \(d\)-orbital splitting energy (\( \Delta\) or \(10 D_q \)) and the strength of field necessary to cause transition between high- and low-spin.

The Tanabe-Sugano diagrams shown below can be used to interpret the spectra of octahedral complexes of a given electron configuration. The diagrams for octahedral complexes for \(d^2, \; d^3, \; d^4, \; d^5, \;  d^6,  \; d^7\) and \(d^8\) are given below. The Tanabe-Sugano diagrams for \(d^0,  \; d^1,  \; d^9\) and \(d^{10}\) are unnecessary. In the case of \(d^0\) and \(d^{10}\), there are no possible \(d-d\) transitions because the \(d\)-orbitals are either completely empty or completely full. In the case of \(d^1\), there is only one free ion term (\(^2D\)) that is split into a ground state \(^2T_{2g}\) and excited state \(^2E_g\). There are no electron-electron repulsions to consider, and there is only one possible transition, so the Tanabe-Sugano diagram is unnecessary for \(d^1\). The case of \(d^9\) is similar and related to \(d^1\) by the "positive hole" concept. In the case of \(d^9\), the lone \(^2D\) free ion term is split into a ground state \(^2E_g\) term and an excited state \(^2T_{2g}\) term. There is just one transition possible and so the Tanabe-Sugano diagram for \(d^9\) is also unnecessary. In some cases, there are two versions given; a complete version and a simplified version. All diagrams are shown in full-page size.

These diagrams can also be used to interpret the electronic spectra of tetrahedral complexes. For a tetrahedral complex with \(d^m\), use the diagram given below for \(d^{10-m}\). All "\(g\)" subscripts on the terms are irrelevant for tetrahedrons.

 

Octahedron with 2 d-electrons

Figure \(\PageIndex{2}\): \(d^2\): Tanabe-Sugano Diagram for octahedral metal complex with two \(d\) electrons. For convenience, terms that can accommodate spin-allowed transitions from the ground state are indicated by solid lines. Terms that have different multiplicity than the ground state are shown in dashed lines.  (CC-BY-SA; Kathryn Haas)

 

 

Octahedron with 3 d-electrons

Figure \(\PageIndex{2}\): \(d^3\): Tanabe-Sugano Diagram for octahedral metal complex with three \(d\) electrons. For convenience, terms that can accommodate spin-allowed transitions from the ground state are indicated by solid lines. Terms that have different multiplicity than the ground state are shown in dashed lines.  (CC-BY-SA; Kathryn Haas) 

 

Octahedron with 4 d-electrons

Figure 3 shows a Tanabe-Sugano diagram that includes all terms. A simplified version of the \(d^4\) Tanabe-Sugano Diagram is shown below in Figure 4.

Figure \(\PageIndex{3}\): \(d^4\), full: Tanabe-Sugano Diagram for octahedral metal complex with four\(d\) electrons. A grey vertical line at 27.2 \(\frac{\Delta_o}{B}\) divides high spin from low spin cases. For convenience, terms that can accommodate spin-allowed transitions from the pentet ground state in high spin (left of grey line) are indicated by heavy solid lines. Terms that can accommodate spin-allowed transitions from the low spin triplet ground state are shown in heavy dashed lines. Terms that have different multiplicity than either pentet or triplet ground states are shown in lighter dotted lines.  For a simplified version of the \(d^4\) diagram, see Figure \(\PageIndex{4}\).  (CC-BY-SA; Kathryn Haas)

 

Figure \(\PageIndex{4}\): \(d^4\), simplified: Tanabe-Sugano Diagram for octahedral metal complex with four\(d\) electrons. A grey vertical line at 27.2 \(\frac{\Delta_o}{B}\) divides high spin from low spin cases. For convenience, terms that can accommodate spin-allowed transitions from the pentet ground state in high spin (left of grey line) are indicated by heavy solid lines. Terms that can accommodate spin-allowed transitions from the low spin triplet ground state are shown in heavy dashed lines. This version of the \(d^4\) Tanabe Sugano Diagram is abbreviated in that it shows only the spin-alloed terms that are most relevant for interpreting UV-visible spectra. For the full version of a \(d^4\) diagram, see Figure \(\PageIndex{3}\). (CC-BY-SA; Kathryn Haas)

 

Octahedron with 5 d-electrons

Figure 5 shows a Tanabe-Sugano diagram that includes all terms. A simplified version of the \(d^5\) Tanabe-Sugano Diagram is shown below in Figure 6.

Figure \(\PageIndex{5}\): \(d^5\), full: Tanabe-Sugano Diagram for octahedral metal complex with five \(d\) electrons. A grey vertical line at 27.3 \(\frac{\Delta_o}{B}\) divides high spin from low spin cases. For convenience, terms that can accommodate spin-allowed transitions from the sextet ground state in high spin (left of grey line) are indicated by heavy solid lines. Terms that can accommodate spin-allowed transitions from the low spin doublet ground state are shown in heavy dashed lines. Terms that have different multiplicity than ground states are shown in lighter dotted lines.   For a simplified version of the \(d^5\) diagram, see Figure \(\PageIndex{6}\).  (CC-BY-SA; Kathryn Haas)

 

Figure \(\PageIndex{6}\): \(d^5\), simple: Tanabe-Sugano Diagram for octahedral metal complex with five \(d\) electrons. A grey vertical line at 27.3 \(\frac{\Delta_o}{B}\) divides high spin from low spin cases. For convenience, terms that can accommodate spin-allowed transitions from the sextet ground state in high spin (left of grey line) are indicated by heavy solid lines. Terms that can accommodate spin-allowed transitions from the low spin doublet ground state are shown in heavy dashed lines. Terms that have different multiplicity than ground states are shown in lighter dotted lines. This version of the \(d^5\) Tanabe Sugano Diagram is abbreviated for simplicity and for the purpose of interpreting UV-visible spectra. For the full version of a \(d^5\) diagram, see Figure \(\PageIndex{5}\)  (CC-BY-SA; Kathryn Haas)

 

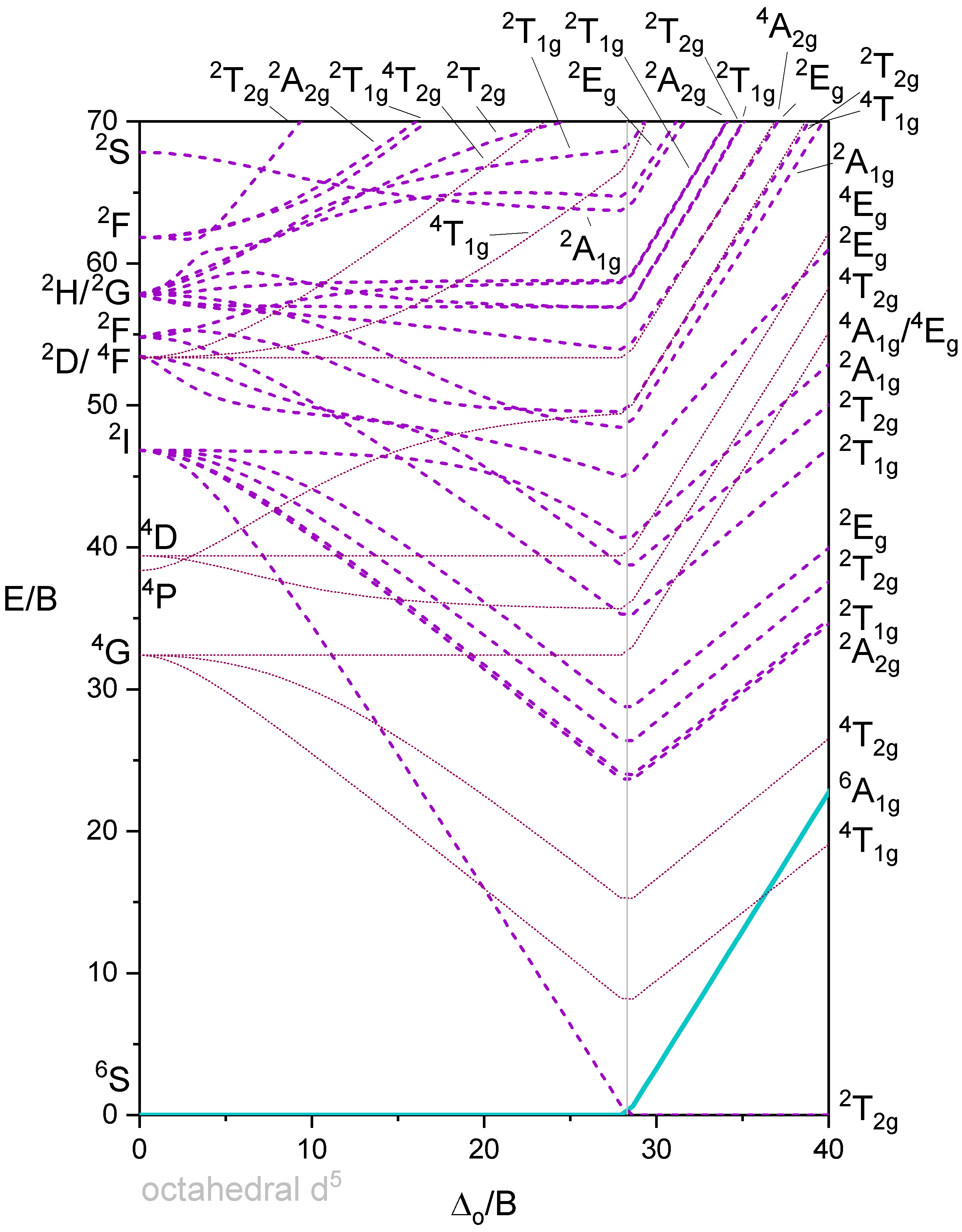
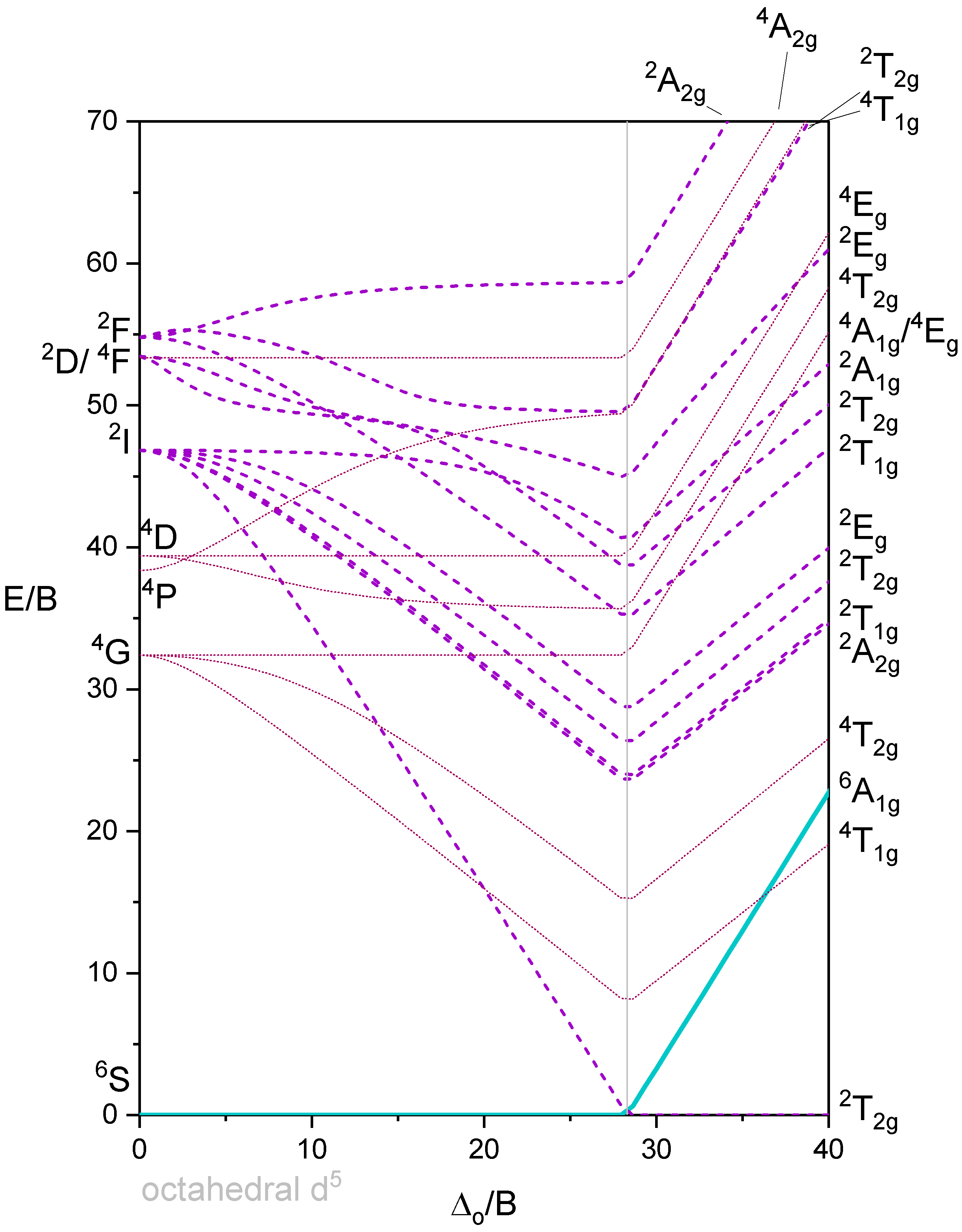
Octahedron with 6 d-electrons

Figure \(\PageIndex{7}\): \(d^6\): Tanabe-Sugano Diagram for octahedral metal complex with six \(d\) electrons. A grey vertical line at 18.5 \(\frac{\Delta_o}{B}\) divides high spin from low spin cases. For convenience, terms that can accommodate spin-allowed transitions from the pentet ground state in high spin (left of grey line) are indicated by heavy solid lines. Terms that can accommodate spin-allowed transitions from the low spin singlet ground state are shown in heavy dashed lines. Terms that have different multiplicity than ground states are shown in lighter dotted lines.  (CC-BY-SA; Kathryn Haas)

 

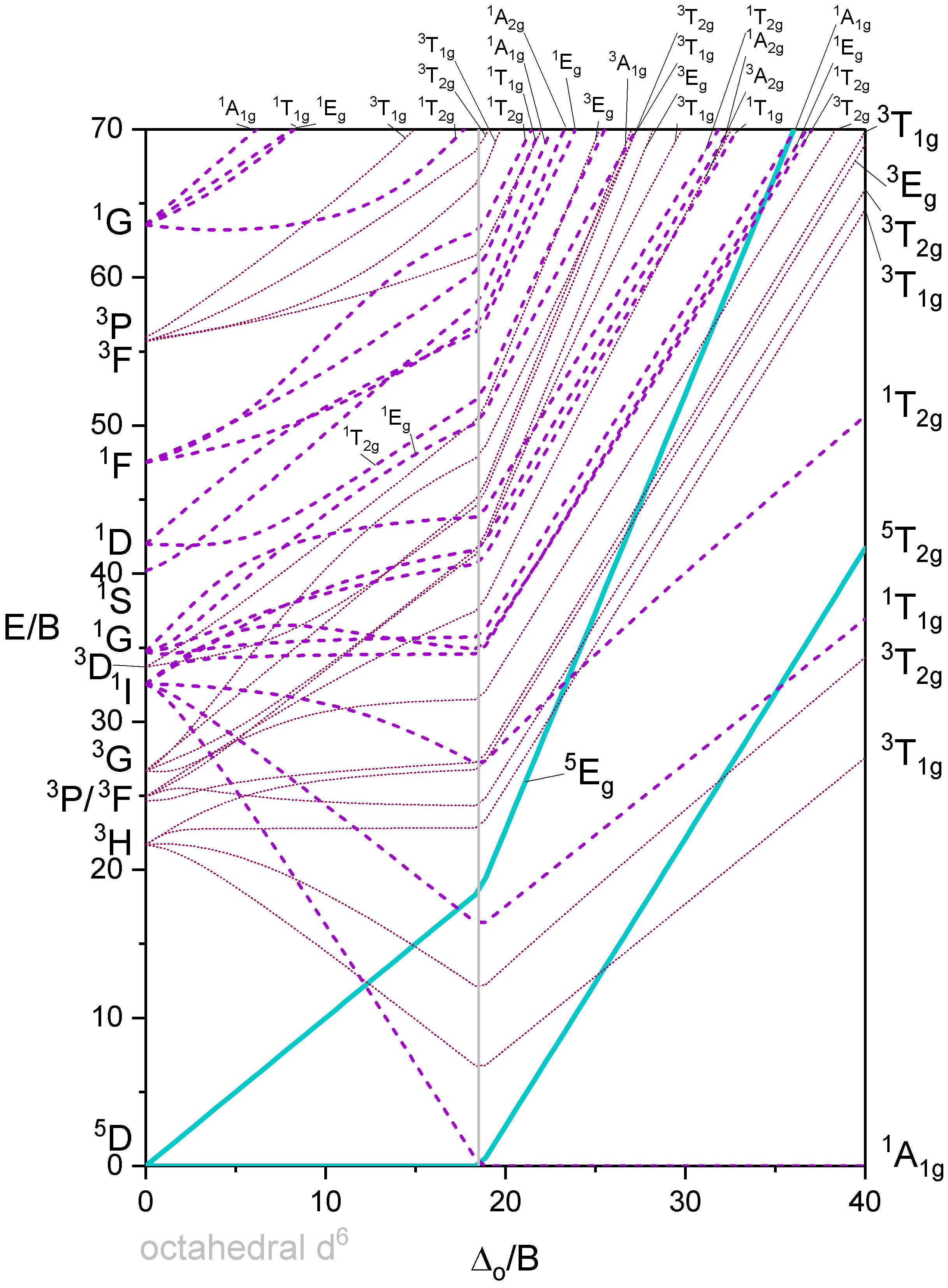
 Octahedron with 7 d-electrons

Figure \(\PageIndex{8}\): \(d^7\): Tanabe-Sugano Diagram for octahedral metal complex with seven \(d\) electrons. A grey vertical line at 21.7 \(\frac{\Delta_o}{B}\) divides high spin from low spin cases. For convenience, terms that can accommodate spin-allowed transitions from the quartet ground state in high spin (left of grey line) are indicated by heavy solid lines. Terms that can accommodate spin-allowed transitions from the low spin doublet ground state are shown in heavy dashed lines.  (CC-BY-SA; Kathryn Haas)

 

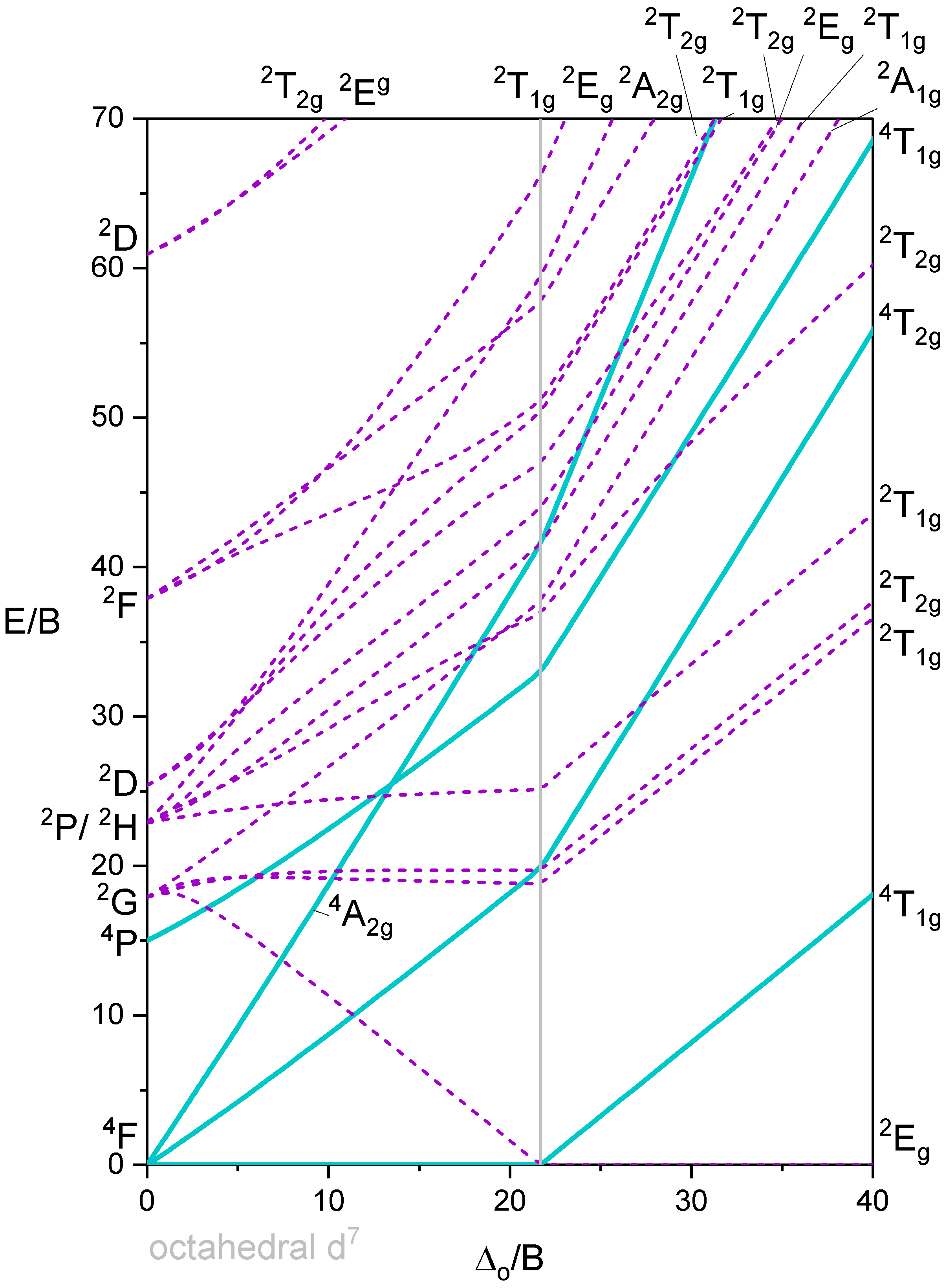
 Octahedron with 8 d-electrons

Figure \(\PageIndex{9}\): \(d^8\): Tanabe-Sugano Diagram for octahedral metal complex with eight\(d\) electrons. For convenience, terms that can accommodate spin-allowed transitions from the ground state are indicated by solid lines. Terms that have different multiplicity than the ground state are shown in dashed lines.  (CC-BY-SA; Kathryn Haas)