8: Reaction Stoichiometry and the Formation of a Metal Ion Complex (Experiment)
- Page ID
- 95877
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To use the method of continuous variation to determine the reaction stoichiometry for the formation of a metal ion complex between iron(II) cations and 1,10-phenanthroline.
- To learn the technique of absorption spectroscopy in order to monitor the relative concentration of a colored metal ion complex in solution.
The net result of a reaction can be summarized by a chemical equation. In order to write a chemical equation, a chemist must identify the reactants and products, as well as the ratios in which these species react and are produced, i.e., the stoichiometry of the reaction.
When two or more reactants are mixed together, it is possible to determine whether a reaction occurs by observing whether any property of the mixture changes. Further, by investigating how the change in an observed property varies when different ratios of reactants are mixed, the stoichiometry of the reaction can be determined.
Consider the study of a reaction where solutions of reactants \(A\) and \(B\) are mixed and product \(P\) is formed:
\[xA+yB \ce{->} zP\]
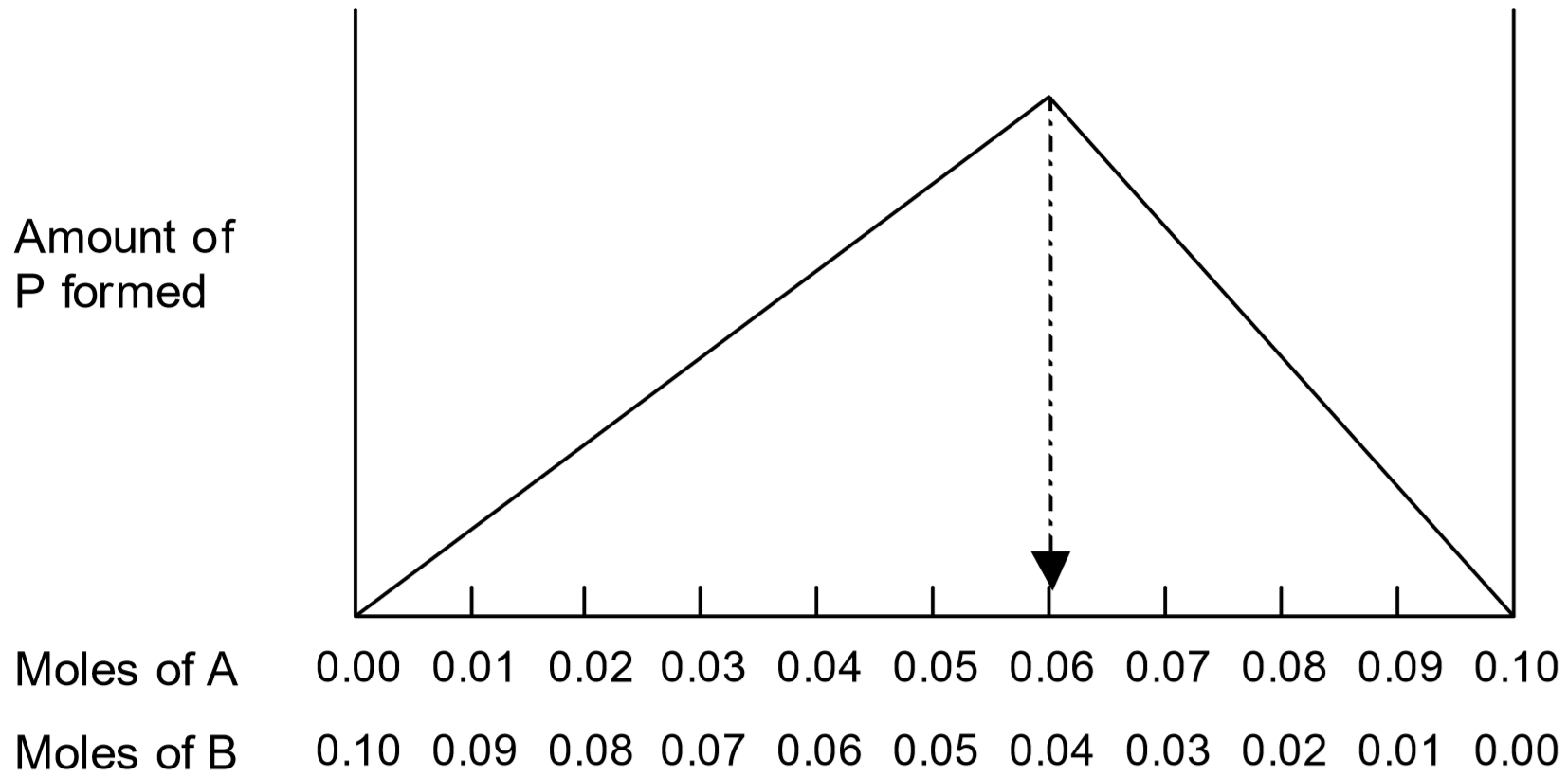
The reactant mixtures are carefully chosen so that sum of the moles of \(A\) and \(B\) are constant, and the amount of product that forms for each mixture is measured. This is known as the method of continuous variation. If either \(A\) or \(B\) is in excess, the excess will remain in solution rather than be used to form product. The maximum amount of \(P\) is formed when \(A\) and \(B\) are mixed in the correct stoichiometric amounts, when there is just enough of each to react with nothing left over.
Suppose for example that \(x = 3\) and \(y = 2\), and that total number of moles of \(A\) and \(B\) is kept fixed at 0.10 moles. The amount of product formed will be at a maximum when the ratio \(A:B\) is 3:2, that is when \(A = 0.06\) moles and \(B = 0.04\) moles:
Note that to the left of the maximum on the plot (\(A < 0.06\) moles), there is not enough of \(A\) to react with all the \(B\) present. Thus, less than the maximum amount of product will be generated. To the right of the maximum (\(B < 0.04\) moles), there is not enough of \(B\) to react with all the \(A\) present. So once again, less than the maximum amount of product will be generated. As long as the total amount of \(A + B\) is constant, the maximum amount of product forms when the \(A:B\) ratio is the stoichiometric ratio for that reaction.
The reaction to be studied in this lab involves the formation of a metal ion complex. Metal ions, especially transition metal ions, possess the ability to form complexes with both organic and inorganic molecules called ligands. These complexes are produced when lone pair electrons from the ligand are donated into empty orbitals of the metal ion (resulting in a coordinate covalent bond). Here, iron(II) cations will be mixed with the ligand 1,10-phenanthroline to produce an iron(II)-phenanthroline complex:
\[x \ce{Fe^{2+}} + y \text{phen} \ce{-> Fe}_x(\text{phen})_{y}^{2+} \]
Where phen = 1,10-phenanthroline =
Using the method of continuous variation as outlined earlier, several reactant solutions are prepared in which the mole quantities of the metal ion and the ligand are varied but the sum of the mole quantities is kept constant. The amount of complex produced will be measured, the maximum indicating when the correct stoichiometric ratio of \(\ce{Fe^{2+}}:\text{phen}\) is used.
In this experiment, both the \(\ce{Fe^{2+}}\) and phenanthroline solutions will have the same molarity concentration. Mixtures prepared with the same total number of moles will therefore have the same total volume (recall that moles of solute can be calculated by multiplying the solution volume by its molarity). As an additional consequence, in each prepared mixture the volume ratio of reactants used will be identical to the mole ratio of reactants used:
\[n_{\ce{Fe}} = M_{\ce{Fe}} \times V_{\ce{Fe}} \]
\[\text{and} \quad n_{\text{phen}} = M_{\text{phen}} \times V_{\text{phen}} \]
\[\text{if} \quad M_{\ce{Fe}} = M_{\text{phen}}\]
\[ \text{then} \quad n_{\ce{Fe}}:n_{\text{phen}} ≡ V_{\ce{Fe}}:V_{\text{phen}}\]
Thus it will be more convenient to analyze the amount of complex product formed as a function of reactant volumes, rather than as a function of reactant moles.
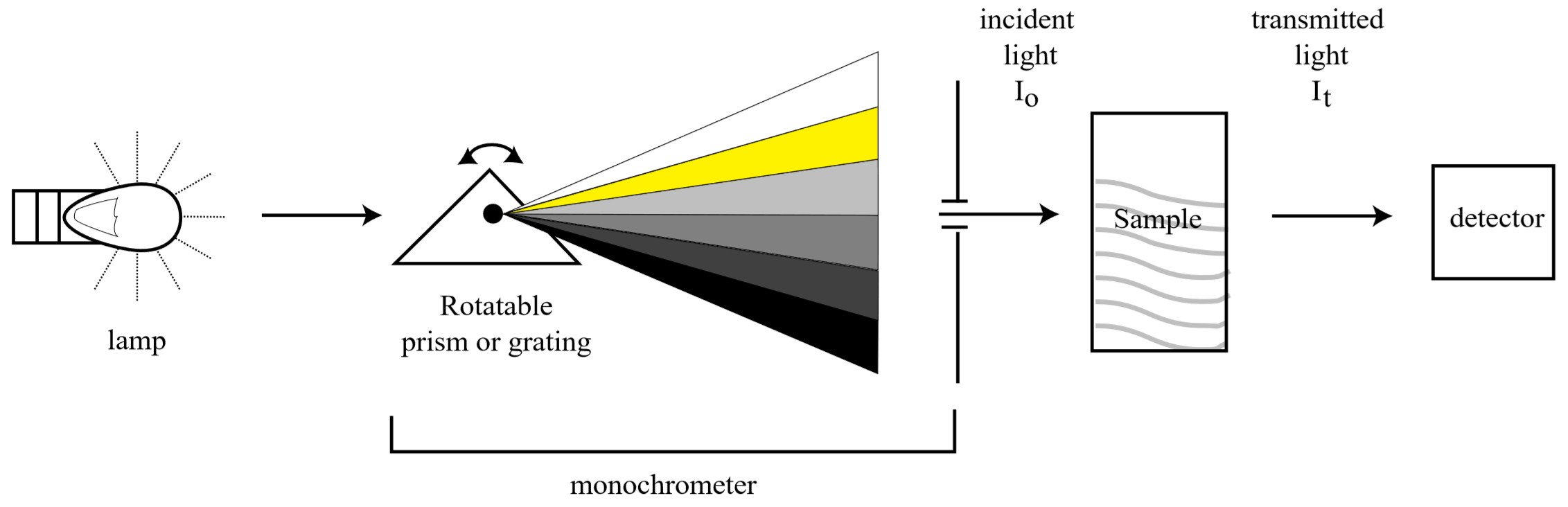
The real challenge in this experiment is choosing an appropriate technique to measure the amount of complex formed. Since the complex is a red-orange color (while both reactants are colorless) the technique of Absorption Spectroscopy will be used. When visible light is directed at a colored compound in solution, the compound will absorb some wavelengths of the light while transmitting other wavelengths. The higher the concentration of the colored compound, the more light it will absorb.
Consider, for example, a blue compound in solution. When visible light is directed at this solution, the compound will predominantly absorb wavelengths in the orange region of the color spectrum, while predominantly transmitting wavelengths in the blue region of the spectrum (note that orange and blue are complementary colors). The transmitted light gives rise to the solution color that we see. Since the iron(II)-phenanthroline complex is a red-orange color, it is expected to absorb blue-green wavelengths, between 460 and 550 nm.
A UV-Visible spectrophotometer is the device used to measure how much light of a specific wavelength is absorbed by a colored species in solution. A schematic diagram of a typical spectrophotometer is shown below:
Where the light absorbed, \(A\), is given by
\[A= \log \frac{I_o}{I_t}\]
Beer’s Law quantitatively describes the relationship between the light absorbed (\(A\)) and the concentration of the colored species in solution (\(c\)) as:
\[A=\varepsilon \times l \times c\]
where \(\varepsilon\) is the molar extinction coefficient (a constant that depends characteristics of the compound analyzed and the wavelength used for analysis) and \(l\) is the path length, or the distance traveled by light through the sample (a constant of 1.0 cm in this experiment). The important thing to note is that concentration and Absorbance are directly proportional. Absorbance can thus be used as a direct measure of the amount of complex produced in each reactant mixture analyzed.
Procedure
Materials and Equipment
50-mL buret, buret stand, two cuvettes for spectrophotometer*, spectrophotometer, eleven small test tubes, two 50-mL beakers, wash bottle filled with distilled water, Parafilm® (or a small stopper), KimWipes®, \(2.50 \times 10^{-4}\) M \(\ce{Fe^{2+}}\) solution and \(2.5 \times 10^{-4}\) M 1,10-phenanthroline solution.
*Items with an asterisk must be checked out from the stockroom.
Both reactant solutions are prepared in an acidic buffer. In addition, 1,10-phenanthroline is a mild irritant. If any of these solutions comes into contact with your skin or eyes, rinse with copious amounts of water for 15 minutes, and inform your instructor.
Experiment Instructions
There will be 4-8 spectrophotometers set out in the lab for student use. Your instructor will provide directions on how to use them correctly at the beginning of the lab session. Students should use the same spectrophotometer to collect all of their data.
Preparing Mixtures of Reactant Solutions
- Obtain approximately 30-mL of \(2.50 \times 10^{-4}\) M \(\ce{Fe^{2+}}\) and 40-mL of \(2.5 \times 10^{-4}\) M phenanthroline in each of your small beakers. Then use your buret to prepare the following solution mixtures in your small test tubes.
- First rinse the buret with distilled water, then with a small amount of the iron(II) solution.
- Drain the appropriate quantities of the iron(II) solution from the buret into each of the eleven test tubes.
- Now rinse the buret with distilled water, then with a small amount of the phenanthroline solution.
- Finally, drain the appropriate amount of phenanthroline from the buret into each test tube.
|
Tube |
iron(II) |
phen |
|---|---|---|
|
1 |
4.50 mL |
0.50 mL |
|
2 |
4.00 mL |
1.00 mL |
|
3 |
3.50 mL |
1.50 mL |
|
4 |
3.00 mL |
2.00 mL |
|
5 |
2.50 mL |
2.50 mL |
|
6 |
2.00 mL |
3.00 mL |
|
7 |
1.50 mL |
3.50 mL |
|
8 |
1.00 mL |
4.00 mL |
|
9 |
0.75 mL |
4.25 mL |
|
10 |
0.50 mL |
4.50 mL |
|
11 |
0.25 mL |
4.75 mL |
- Mix each solution well by covering the tube with Parafilm (or a small stopper) and inverting it many times. The red-orange color of the iron(II)-phenanthroline complex should fully develop about ten minutes after mixing.
Determining \(\lambda_{max}\) of the Complex
- Rinse the two cuvettes with distilled water and dry them carefully with a KimWipe tissue. Fill the first cuvette to the mark with phenanthroline only. This solution will be used as your calibration blank. Then fill the second cuvette to the mark with the solution mixture in tube #5 (containing equal volumes of \(\ce{Fe^{2+}}\) and phenanthroline). This mixture will be used to determine the wavelength of maximum absorption of the complex product.
- Adjust the Absorbance reading on the spectrophotometer to zero using the phenanthroline blank in the sample holder. Then measure the absorbance of reactant mixture #5 between 460 nm and 550 nm at 10 nm intervals. Note that each time the wavelength is changed the instrument must be recalibrated to zero with the blank. Record this data on your report form, and identify the wavelength of maximum absorbance of the complex (\(\lambda_{max}\)).
- Return reaction mixture #5 in the second cuvette into its original test tube. Then rinse this cuvette with distilled water and carefully dry it. You will use this cuvette for all subsequent absorbance measurements.
Measuring the Absorbance of the Solutions with Different Mole/Volume Ratios
- Set the wavelength of the spectrophotometer to \(\lambda_{max}\) and again recalibrate it to zero using the blank. Since all remaining measurements will be taken at this wavelength only, no further recalibration is required.
- Measure the absorbance of each of the eleven prepared solution mixtures. Record this data on your report form.
- Fill the clean, empty cuvette to the mark with the solution mixture in tube #1. Place it in the sample holder and measure the solution absorbance.
- Return the solution mixture into its original test tube. Rinse this cuvette with distilled water and carefully dry it.
- Repeat this process with all other solution mixtures in tubes #2-11.
- When completely finished, dispose of your chemical waste as directed by your instructor.
Data Analysis
Using Microsoft Excel©, graph your absorbance data as a function of the volume of ligand used. You will need to graph this data as two data sets with overlay. Treat ascending and descending values as two separate data sets, plotting them both on the same set of axes. If necessary, review the instructions provided for the Excel Exercise performed at the beginning of the semester.
Add best-fit trendlines to both data sets, and obtain the equations of these trendlines. Then solve for the point of intersection of these lines using your two equations in a simultaneous equations calculation.
From the point of intersection you can determine the volume mixture of reactants used to obtain the maximum absorbance (hence the maximum amount of complex formed). Finally, using this volume mixture, you can determine the simplest whole number volume ratio of \(\ce{Fe^{2+}}:\text{Ph}\) (identical to the mole ratio), which is the stoichiometric ratio for this reaction.
Prelab Assignment: Reaction Stoichiometry and the Formation of a Metal Ion Complex
- The method of continuous variation was used to determine the stoichiometry for:
\[xA(aq) + yB(aq) \ce{->} zP(aq)\]
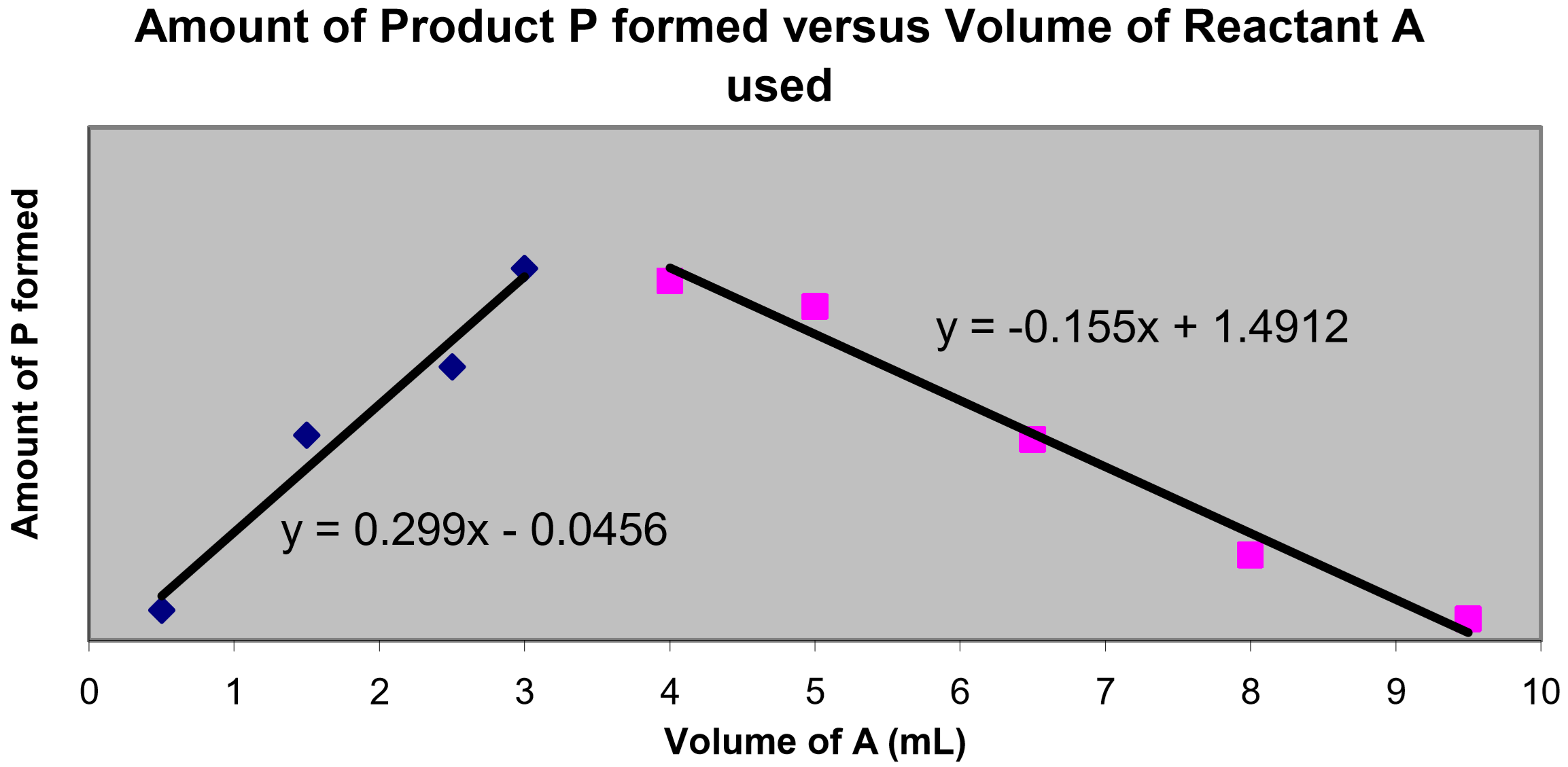
In this experiment, the molarity concentrations of reactants \(A\) and \(B\) are both \(1.50 \times 10^{-3}\) M. The amount of product was measured for a variety of mixtures of \(A\) and \(B\), where the total mixture volume was always kept constant at 10.0 mL. The following plot was generated:
- Using the equations of the trendlines, perform a simultaneous equations calculation to determine the volume of \(A\) used to obtain the maximum amount of product (= the value of \(x\) at the point of intersection of the lines).
- Determine the volume of \(B\) used to obtain the maximum amount of product (hint – what was the total volume of the mixture of \(A\) and \(B\)?).
- Using these two volumes, determine the simplest whole number volume ratio of reactants (\(\text{volume } A : \text{volume } B\)) used to obtain the maximum amount of product. Note that this ratio yields the reaction stoichiometry, i.e., \(\text{volume } A : \text{volume } B ≡ x : y\).
- In the experiment to be performed in this lab, what is the unbalanced reaction that will be studied?
- What technique will be used in this experiment to determine the amount of product produced?
- What special feature of the product makes this a good technique to use?
Lab Report: Reaction Stoichiometry and the Formation of a Metal Ion Complex
Experimental Data
Determination of \(\lambda_{max}\) of the Iron(II)-Phenanthroline Complex
Using Solution Mixture 5:
|
Wavelength (nm) |
Absorbance (unitless) |
Wavelength (nm) |
Absorbance (unitless) |
|---|---|---|---|
|
460 |
510 |
||
|
470 |
520 |
||
|
480 |
530 |
||
|
490 |
540 |
||
|
500 |
550 |
- Wavelength of Maximum Absorbance of the metal ion-ligand complex, \(\lambda_{max}\) = nm
Absorbance of Reactant Solution Mixtures
Molarity of Iron(II):
Molarity of Phenanthroline:
|
Mixture |
Volumes of Reactants Mixed (mL) |
Absorbance (unitless) |
|
|---|---|---|---|
| -- |
Iron(II) |
Phenanthroline |
-- |
|
1 |
4.50 |
0.50 |
|
|
2 |
4.00 |
1.00 |
|
|
3 |
3.50 |
1.50 |
|
|
4 |
3.00 |
2.00 |
|
|
5 |
2.50 |
2.50 |
|
|
6 |
2.00 |
3.00 |
|
|
7 |
1.50 |
3.50 |
|
|
8 |
1.00 |
4.00 |
|
|
9 |
0.75 |
4.25 |
|
|
10 |
0.50 |
4.50 |
|
|
11 |
0.25 |
4.75 |
|
Data Analysis
- Using Microsoft Excel©, create a graph of “Absorbance versus Volume of Phenanthroline used”. Plot this data as two data sets with overlay. Treat ascending and descending values as two separate data sets, plotting them both on the same set of axes (if needed, review the instructions provided for the Excel Exercise performed at the beginning of the semester). Add best-fit trendlines to both data sets, and obtain the equations of these trendlines. Attach this graph to your report form.
- Ascending data trendline equation:
- Descending data trendline equation:
- Using the equations of the trendlines, perform a simultaneous equations calculation to determine the volume of phenanthroline used to achieve the maximum product absorbance (= the value of \(x\) at the point of intersection of the lines). Show your work below.
- Determine the volume of iron(II) used to achieve the maximum product absorbance (hint, what was the total volume of the iron(II)–phenanthroline mixture?).
- Using these two reactant volumes (at the maximum absorbance) determine the simplest whole number volume ratio of \(\ce{Fe^{2+}}:\text{phen}\), which is the stoichiometric ratio for this reaction.
- Write the balanced equation for the reaction studied in this lab.
- Since the two reactant solutions in this experiment have the same molarity, the volume ratio at maximum absorbance will be the same as the mole ratio at maximum absorbance. Perform appropriate calculations to prove that this is indeed the case.