10: Experimental Determination of the Gas Constant (Experiment)

Last updated
Save as PDF

Page ID: 93994

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objectives

To experimentally determine the value of the Gas Constant, \(R\)
To practice using the Gas Laws to solve a variety of problems.

A gas is the state of matter that is characterized by having neither a fixed shape nor a fixed volume. Gases exert pressure, are compressible, have low densities and diffuse rapidly when mixed with other gases. On a microscopic level, the molecules (or atoms) in a gas are separated by large distances and are in constant, random motion.

Four measurable properties can be used to describe a gas quantitatively: pressure (\(P\)), volume (\(V\)), temperature (\(T\)) and mole quantity (\(n\)). The relationships among these properties are summarized by the Gas Laws, as shown in the table below.

Charles’s Law	\(V \propto T\)	\(P\) and \(n\) are held constant As gas temperature increases, gas volume increases.	\(\displaystyle \frac{V_1}{T_1}=\frac{V_2}{T_2}\)
Boyle’s Law	\(V \propto \frac{1}{P}\)	\(T\) and \(n\) are held constant As gas pressure increases, gas volume decreases.	\(\displaystyle P_1V_1=P_2V_2\)
Avogadro’s Law	\(V \propto n\)	\(P\) and \(T\) are held constant As the number of moles of gas increase, gas volume increases.	\(\displaystyle \frac{V_1}{n_1}=\frac{V_2}{n_2}\)
Combined Law	\(V \propto \frac{T}{P}\)	\(n\) is held constant Obtained by combining Boyle’s Law and Charles’s Law.	\(\displaystyle \frac{P_1V_1}{T_1}=\frac{P_2V_2}{T_2}\)

A closer look at the Combined Law reveals that the volume of a gas depends on both the pressure and temperature. Thus, if the volumes of two gases are to be compared, they must be under the same \(P\) and \(T\). A commonly used set of \(P\) and \(T\) reference conditions is known as Standard Temperature and Pressure, or STP. Standard temperature is defined as exactly 0 °C (273 K) and standard pressure is defined as exactly 1 atm (760 mmHg).

The Ideal Gas Law is obtained by combining Boyle’s Law, Charles’s Law and Avogadro’s Law together:

\[PV = nRT\]

Here, \(P\) represents as the gas pressure (in atmospheres); \(V\) is the gas volume (in Liters); \(n\) is the number of moles of gas in the sample; \(T\) is the gas temperature (in Kelvins). \(R\) is a proportionality constant called the Gas Constant, and has a theoretical value of 0.08206 \(\frac{L \cdot atm}{mol \cdot K}\). Note that the units of \(R\) will allow the units of \(P\), \(V\), \(n\) and \(T\) in the Ideal Gas Law to cancel correctly.

In this lab, students will measure various properties of a sample of hydrogen gas in order to experimentally determine the value of the Gas Constant, \(R\). The single displacement reaction between magnesium metal and hydrochloric acid will be used to generate the hydrogen gas:

\[\ce{Mg(s) + 2HCl(aq) -> MgCl2 (aq) + H2 (g)}\]

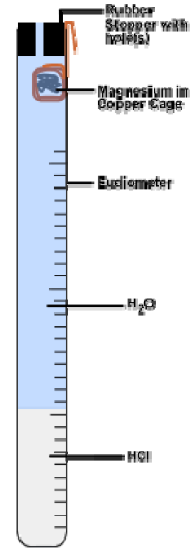
The hydrogen gas will be collected in a eudiometer, a tube closed at one end and marked in milliliter volume units. The gas will be collected in the closed end of the tube over a water bath via the technique of water displacement (see figures below)

Students will then obtain the following values for the collected sample of hydrogen gas: (1) Volume, (2) Temperature, (3) Moles, and (4) Pressure. The hydrogen volume will be directly measured from the eudiometer scale. The hydrogen temperature will also be directly measured using a thermometer. However, the mole quantity and pressure of the hydrogen gas must be determined indirectly. The mole quantity of the collected hydrogen can be easily calculated from the measured mass of the magnesium reactant using stoichiometry. But the hydrogen pressure is a little more difficult to obtain. Since hydrogen is collected over a water bath, a small amount of water vapor is mixed with the hydrogen in the eudiometer. The combined pressure of the \(\ce{H2}\) and \(\ce{H2O}\) gases will be equal (after adjustments) to the external atmospheric pressure:

\[P_{atm} = P_{hydrogen} + P_{water vapor}\]

\(P_{atm}\) (atmospheric pressure) will be measured using a barometer. \(P_{water vapor}\) (the partial pressure of water vapor) depends on the temperature of the water bath, and can be obtained from the table supplied below. By substituting these values in the above equation, the pressure of hydrogen \(P_{hydrogen}\)) will be determined.

Temperature (°C)	\(P_{\text{water vapor}}\) (mmHg)
16	13.5
17	14.5
18	15.5
19	16.5
20	17.5
21	18.7
22	19.3
23	21.1
24	22.4
25	23.8
26	25.2
27	26.7
28	28.3
29	30.0

Finally, to determine the value of the Gas Constant (\(R\)), the quantities \(V\), \(T\), \(n\) and \(P\) obtained for the hydrogen gas must simply be substituted into the Ideal Gas Equation. Students can then evaluate their accuracy in this experiment by comparing their experimental result to the true theoretical value of \(R\), and by calculating their percent error.

Procedure

Materials and Equipment

4.0-cm ribbon of magnesium, length of copper wire (reusable), 6 M \(\ce{HCl}\) (aq), 50-mL eudiometer*, eudiometer stopper with hole(s)*, burette stand, large beaker, thermometer, small funnel, small graduated cylinder, barometer, large tub of water, electronic balance and sandpaper.

Safety

Concentrated \(\ce{HCl}\) is dangerous! Handle it with extreme care as demonstrated by your instructor. If any spills occur, inform your instructor immediately. Wash under running water (sink or shower) and use the neutralizing sodium bicarbonate solution supplied at the sinks if necessary. Also note that hydrogen gas is flammable, so be sure to have no open flames nearby when you perform this experiment.

Experimental Procedure

Magnesium Ribbon

Obtain a 4.0-cm ribbon of magnesium (\(\ce{Mg}\)), a piece of sandpaper, and a length of copper wire.
Carefully sand the outside of the \(\ce{Mg}\) ribbon to remove any oxide coating. Do not sand on the bench top! Place the \(\ce{Mg}\) ribbon on a paper towel while sanding. Weigh the cleaned \(\ce{Mg}\) ribbon and record this mass on your report form. Note that this mass should be less than 0.040 grams. If it is heavier, your \(\ce{Mg}\) ribbon will have to be “trimmed” by your instructor.
Wrap the \(\ce{Mg}\) around the end of the copper wire. Do this in a tight ball with only a small gap between layers. Then wrap the copper wire to form a cage around the \(\ce{Mg}\) ball. The cage must be tight enough to keep the \(\ce{Mg}\) inside, but loose enough to allow water to easily flow around the wire. Roughly 3-cm of copper wire should be left over as a “handle” (see Figure 1).

Eudiometer Set Up and Reaction

Obtain a eudiometer tube and stopper (with holes) from the stockroom. Use the burette clamp to hold it in place, open end up.
Add ~10-mL of 6 M \(\ce{HCl}\) (aq) to the eudiometer tube using a small funnel. Then add tap water to the eudiometer carefully until it is filled to the brim (see Figure 1).
Hang the \(\ce{Mg}\) ball inside the open end of the eudiometer, ~2-cm down from the top. Then insert the stopper into this end, and, while holding it in place, quickly invert the entire tube into your largest beaker 3⁄4 filled with water. Clamp the tube in the water in the upside down position (see Figure 2).
The reaction will occur as soon as the acid diffuses down the tube and reaches the \(\ce{Mg}\) ribbon. As hydrogen gas is generated it will fill the eudiometer by forcing the water out of the tube and into the beaker via water displacement (see Figure 2). Allow the reaction to proceed until no \(\ce{Mg}\) is left and no further gas is formed. This should take 3-5 minutes.

Pressure Equalization

To ensure that the pressure of hydrogen (and water vapor) in the eudiometer is equal to atmospheric pressure, the level of the water inside the tube must be the same as the level of water outside the tube. To achieve this, transfer both the tube and the beaker of water into the large bucket of water in the sink. Then raise or lower the tube until the internal and external water levels are equal.

Measurements

After equalizing the water levels, record the following measurements:

The volume of hydrogen gas collected (read directly from the eudiometer scale), in mL
The temperature of the hydrogen gas collected, in °C. This can be measured by first removing the stopper then placing the thermometer directly in the eudiometer (keep the tube inverted so the gas does not readily escape). It is also acceptable to assume that the temperature of the hydrogen gas is the same as the temperature of the water bath, especially if you wait a while before making your measurements.
The atmospheric pressure (use the lab barometer), in mmHg
The temperature of the water in the plastic tub (use the thermometer), in °C
The vapor pressure of water at the above temperature (obtain from Table on page 2), in mmHg

When finished, repeat this entire procedure a second time with a fresh piece of magnesium ribbon.

Figure 1: Before Inverting

Figure 2: After Inverting

Pre-laboratory Assignment: Experimental Determination of the Gas Constant

What is the name of the gas that will be collected and studied in this lab? Write the balanced equation for the reaction used to generate this gas.

You will perform several measurements on your collected gas sample in order to experimentally determine the value of the Gas Constant (\(R\)).

What is the theoretical value of \(R\), and what are its units?
The Gas Constant is found in the Ideal Gas Law. Write the equation for this law.

The magnesium ribbon used in this reaction must be carefully handled.

What must you avoid doing with the magnesium ribbon at the lab bench (hint, see Procedure #2)?
What mass of the magnesium ribbon should be used

What is the name of the specialized "tube" that your gas is collected in?

This tube not only collects the gas, it also allows you to directly measure the gas (circle one): pressure / temperature / volume

Consider some of the other equipment you will use in this lab.

What device will you use to measure atmospheric pressure?
What TWO temperatures will you measure with your thermometer?

Part of the procedure for this experiment involves ensuring that the total pressure of gases collected inside the specialized tube is equal to atmospheric pressure. How is this achieved (hint, see Procedure #8)?

Lab Report: Experimental Determination of the Gas Constant

Experimental Data

	Trial 1	Trial 2
Mass of Magnesium metal used
Volume of \(\ce{H2}\) gas collected
Temperature of \(\ce{H2}\) gas collected
Atmospheric Pressure
Temperature of Water in bath (bucket)
Vapor Pressure of Water at above temperature

Data Analysis

Using your experimental data, determine the value of \(R\), the gas constant. Show all your conversions and calculations for each step clearly in the table below. Pay attention to units and significant figures.

	Trial 1	Trial 2
Volume of \(\ce{H2}\) gas (in L)
Temperature of \(\ce{H2}\) gas (in K)
Moles of \(\ce{H2}\) gas
Pressure of \(\ce{H2}\) gas (in atm)
Experimental value of \(R\) (include units)

Average value of \(R\) (include units):
Percent Error between your average value and the theoretical value of \(R\) (show work):

Questions

The hydrogen generated in this lab was a product of the reaction between magnesium and hydrochloric acid. Which of these reactants was the limiting reactant? Provide experimental evidence to support your choice.

Suppose when you inverted the eudiometer, a bubble of air became trapped inside it. Would this make your experimental value of \(R\) larger, smaller, or have no effect? Briefly explain your response.

In Santa Monica, a sample of dry hydrogen gas inflates a balloon to 43.0 mL at 761 torr (sea-level). If the temperature remains unchanged, what is the balloon’s volume (in mL) in Denver, where the pressure is 12.2 psi (5000 ft elevation)? Assume that no gas has been added or removed.

Another balloon is inflated to a volume of 1.250 L with dry hydrogen gas, at 28.0 °C. The balloon is then cooled, and its volume drops to 964 mL. If the pressure is unchanged, what is the hydrogen gas temperature (in °C) in the cooled balloon? Assume that no gas has been added or removed.

Yet another balloon is inflated to a volume of 434 cm ³ using 0.141 moles of dry hydrogen gas. An additional 0.129 grams of hydrogen is then injected into the balloon at constant pressure and temperature. Calculate the new volume of the balloon (in cm ³).

Hydrogen gas can be generated from the reaction between aluminum metal and hydrochloric acid:

\[\ce{2Al (s) + 6HCl (aq) -> 2AlCl3 (aq) + 3H2 (g)}\]

Suppose that 3.00 grams of \(\ce{Al}\) are mixed with excess acid. If the hydrogen gas produced is directly collected into a 850. mL glass flask at 24.0 °C, what is the pressure inside the flask (in atm)?

This hydrogen gas is then completely transferred from the flask to a balloon. To what volume (in L) will the balloon inflate under STP conditions?

Suppose the balloon is released and rises up to an altitude where the temperature is 11.2 °C and the pressure is 438 mmHg. What is the new volume of the balloon (in L)?