Insoluble Salts
- Page ID
- 36265
- Define Ksp, the solubility product.
- Explain solid/solution equilibria using \(K_{sp}\) and Qsp.
- Calculate molarity of saturated solution from Ksp.
- Calculate \(K_{sp}\) from molarity of saturated solution.
Phase transitions such as sublimation, deposition, melting, solidification, vaporization, and condensation are heterogeneous equilibria; so are the formation of crystals from a saturated solution, because a solid and its solution are separated phases. The picture shown here is the formation of solid from a gaseous solution. The equilibrium constants for saturated solution and solid formation (precipitate) are called solubility product, Ksp. For unsaturated and supersaturated solutions, the system is not at equilibrium, and ion products, Qsp, which have the same expression as Ksp, are used.
An oversaturated solution becomes a saturated solution by forming a solid to reduce the dissolved material. The crystals formed are called a precipitate. Often, however, a precipitate is formed when two clear solutions are mixed. For example, when a silver nitrate solution and sodium chloride solution are mixed, silver chloride crystals \(\ce{AgCl_{\large{(s)}}}\) (a precipitate) are formed. \(\ce{Na+}\)and \(\mathrm{\sideset{ }{_{3}^{-}}{NO}}\) are spectator ions.
\[\mathrm{Ag^+_{\large{(aq)}} + \sideset{ }{_{\large{(aq)}}^{-}}{Cl} \rightarrow AgCl_{\large{(s)}}} \hspace{10px} \ce{(precipitate)}\]
Silver chloride is one of the few chlorides that has a limited solubility. A precipitate is also formed when sodium carbonate is added to a sample of hard water,
\[\mathrm{Ca^{2+}_{\large{(aq)}} + CO^{2-}_{3\large{(aq)}} \rightarrow CaCO_{3\large{(s)}}} \hspace{10px} \ce{(precipitate)}\]
When a solid dissolves, we have the reverse reaction:
\[\mathrm{AgCl_{\large{(s)}} \rightarrow Ag^+_{\large{(aq)}} + \sideset{ }{_{\large{(aq)}}^{-}}{Cl}} \hspace{10px} \ce{(dissolving)}\]
\[\ce{CaCO_{3\large{(s)}} \rightarrow Ca^2+_{\large{(aq)}} + CO^{2-}_{3\large{(aq)}}} \hspace{10px} \ce{(dissolving)}\]
Solubility Products, Ksp, and Ion Products Qsp
Formations of precipitates are chemical equilibria phenomena, and we usually write these heterogeneous equilibrium in the following manner, and call the equilibrium constants solubility products, Ksp:
| Equilibrium | Expression for \(K_{sp}\) and Qsp |
|---|---|
| \(\ce{AgCl_{\large{(s)}} \rightleftharpoons Ag+_{\large{(aq)}} + Cl^{-}_{\large{(aq)}}}\) | \(\ce{[Ag+] [Cl- ]}\) |
| \(\ce{CaCO_{3\large{(s)}} \rightleftharpoons Ca^2+_{\large{(aq)}} + CO^{2-}_{3\large{(aq)}}}\) | \(\ce{[Ca^2+] [CO3- ]}\) |
| \(\ce{Li2CO_{3\large{(s)}} \rightleftharpoons 2 Li+_{\large{(aq)}} + CO^{2-}_{3\large{(aq)}}}\) | \(\ce{[Li+]^2 [CO3- ]}\) |
The solubility product, Ksp, is a special type of equilibrium constant given to a solution containing sparingly soluble salts. The symbols (aq) indicate that these ions are surrounded by water molecules; these ions are in the solution. Note the expression for the solubility product given above, please. These are special equilibrium constants, because the solid present has a constant tendency of being dissolved. Therefore, their role in \(K_{sp}\) is a constant. They do not appear in the \(K_{sp}\) expression. If the solution is not saturated, no precipitate will form. In this case, the product is called the ion product, Qsp, which is the product of the concentrations of the ions at any moment in time. and is equal to the solubility product for the salt when at equilibrium.
The Table of solubility product is given as Salt, \(K_{sp}\) in the Handbook Section. In this table, the salts are divided into
- Carbonates, salts of \(\ce{CO3^2-}\)
- Chromates, salts of \(\ce{CrO4^2-}\)
- Halides, salts of \(\ce{Cl-}\), \(\ce{Br-}\), and \(\ce{I-}\)
- Hydroxides, salts of \(\ce{OH-}\)
- Oxalates, salts of \(\ce{C2O4^2-}\)
- Sulfates, salts of \(\ce{SO4^2-}\)
- Sulfides, salts of \(\ce{S^2-}\)
Qsp, \(K_{sp}\) and Saturation
For some substances, formation of a solid or crystallization does not occur automatically whenever a solution is saturated. These substances have a tendency to form oversaturated solutions. For example, syrup and honey are oversaturated sugar solutions, containing other substances such as citric acids. For oversatureated solutions, Qsp is greater than Ksp. When a seed crystal is provided or formed, a precipitate will form immediately due to equilibrium of requiring Qsp to approach Ksp.
Sodium acetate trihydrate, \(\ce{NaCH3COO\cdot 3H2O}\), when heated to 370 K will become a liquid. The sodium acetate is said to be dissolved in its own water of crystallization. The substance stays as a liquid when cooled to room temperature or even below 273 K. As soon as a seed crystal is present, crystallization occurs rapidly. In such a process, heat is released, and the liquid feels warm. Thus, the relationship among Qsp, \(K_{sp}\) and saturation is given below:
| Qsp < Ksp | Unsaturated solution |
|---|---|
| Qsp = Ksp | Saturated solution |
| Qsp > Ksp | Oversaturated solution |
Molar Solubilities and Solubility Products
Solubility products, Ksp, of salts are indirect indications of their solubilities expressed in mol/L (called molar solubility). However, the solubility products are more useful than molar solubility. The molar solubilities are affected when there are common ions present in the solution. We need to employ the solubility products to estimate the molar solubilities in these cases. When a salt is dissolved in pure water, solubility products and molar solubilities are related. This is illustrated using calcium carbonate. If x is the concentration of \(\ce{Ca^2+}\) (= \(\ce{[CO3^2-]}\)) in the saturated solution, then
\[K_{\ce{sp}} = x^2\]
In this case, x is also called the molar solubility of \(\ce{CaCO3}\). The following examples illustrate the relationship between solubility products, Ksp, and molar solubilities.
The \(K_{sp}\) for \(\ce{AgCl}\) is 1.8e-10 M2. What is the molar solubility of \(\ce{AgCl}\) in pure water?
Solution
Let x be the molar solubility, then
\(\begin{array}{ccccc}
\ce{AgCl &\rightleftharpoons &Ag+ &+ &Cl-}\\
&&x &&x
\end{array}\)
\(\begin{align}
x &= (\textrm{1.8e-10 M}^2)^{1/2}\\
&= \textrm{1.3e-5 M}
\end{align}\)
 DISCUSSION
DISCUSSION
The solubility product, \(K_{sp}\) is a better indicator than the usual solubility specification of g per 100 mL of solvent or moles per unit volume of solvent.
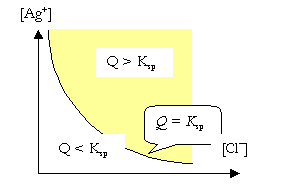
For the \(\ce{AgCl}\) case, when the cation concentration is not the same as the anion concentration (\(\ce{[Ag+] \neq [Cl- ]}\)), solubility of \(\ce{AgCl}\) can not be defined in terms of moles per L. In this case, the system can be divided into three zones. The condition \(\ce{[Ag+] [Cl- ]} = K_{\ce{sp}}\), is represented by a line which divides the plane into two zones.
When \(\ce{[Ag+] [Cl- ]} < K_{\ce{sp}}\), no precipitate will be formed.
When \(\ce{[Ag+] [Cl- ]} > K_{\ce{sp}}\), a precipitate will be formed.
When \(\ce{AgCl}\) and \(\ce{NaCl}\) dissolve in a solution, both salts give \(\ce{Cl-}\) ions. The effect of \(\ce{[Cl- ]}\) on the solubility of \(\ce{AgCl}\) is called the Common Ion Effect.
The \(K_{sp}\) for \(\ce{Ag2CrO4}\) is 9e-12 M3. What is the molar solubility of \(\ce{Ag2CrO4}\) in pure water?
Solution
Let x be the molar solubility of \(\ce{Ag2CrO4}\), then
\(\begin{array}{ccccc}
\ce{Ag2CrO4 &\rightleftharpoons &2 Ag+ &+ &CrO4^2-}\\
&&2 x &&x
\end{array}\)
\((2 x)^2 (x) = K_{\ce{sp}}\)
\(\begin{align}
x &= \left (\dfrac{\textrm{9e-12}}{4} \right )^{1/3}\\
&= \textrm{1.3e-4 M}
\end{align}\)
\(\ce{[Ag+]} = \textrm{2.6e-4 M}\)
and the molar solubility is 1.3e-4 M.
DISCUSSION
A similar diagram to the one given for \(\ce{AgCl}\) can be drawn, but the shape of the curve representing the \(K_{sp}\) is different.
The \(K_{sp}\) for \(\ce{Cr(OH)3}\) is 1.2e-15 M4. What is the molar solubility of \(\ce{Cr(OH)3}\) in pure water?
Solution
Let x be the molar solubility of \(\ce{Cr(OH)3}\), then you have
\(\begin{array}{ccccc}
\ce{Cr(OH)3 &\rightleftharpoons &Cr^3+ &+ &3 OH-}\\
&&x &&3 x
\end{array}\)
Thus,
\(\begin{align}
x (3 x)^3 &= \textrm{1.2e-15}\\
x &= \left (\dfrac{\textrm{1.2e-15}}{27} \right )^{1/4}\\
&= \textrm{8.2e-5 M}
\end{align}\)
Very careful experiment indicates that the molar solubility of \(\ce{Bi2S3}\) is 1.8e-15 M; what value of \(K_{sp}\) does this compound have?
Solution
If the molar solubility of \(\ce{Bi2S3}\) is 1.8e-15, then
\(\begin{array}{ccccc}
\ce{Bi2S3 &\rightleftharpoons &2 Bi^3+ &+ &3 S^2-}\\
&&\textrm{3.6e-15} &&\textrm{5.4e-15}
\end{array}\)
\(\begin{align}
K_{\ce{sp}} &= (\textrm{3.6e-15})^2 (\textrm{5.4e-15})^3\\
&= \textrm{2.0e-72 M}^5
\end{align}\)
DISCUSSION
You should be able to calculate the \(K_{sp}\) if you know the molar solubility.
Review of skills
- Be able to write the \(K_{sp}\) expression for the ionization of any salts, and calculate \(K_{sp}\) from molar solubility.
- Calculate \(K_{sp}\) from molar solubility and vice versa. Pay attention to the stoichiometry of the salt. You may have to understand what the salt really is in order to know how they ionize in the solution. You have learned the method to calculate molar solubility from Ksp.
- Perform calculations and be able to tell if a precipitate will form. The calculation is an important part of chemistry.
Questions
- Experiment shows that the molar solubility of \(\ce{CuCl}\) is \(1.1 \times 10^{-3}\). What is its solubility product, Ksp?
- The \(K_{sp}\) for \(\ce{Hg2I2}\) is \(4.5 \times 10^{-29}\). What is its molar solubility in pure water? Remember \(\ce{Hg2^2+}\) is a stable ion in solution.
- What is the pH in a saturated solution of \(\ce{Ca(OH)2}\)?\(K_{sp} = 5.5 \times 10^{-6}\) for \(\ce{Ca(OH)2}\).
- Chemical analysis gave \(\ce{[Pb^2+]} = \textrm{0.012 M}\), and \(\ce{[Br- ]} = \textrm{0.024 M}\) in a solution. From a table, you find \(K_{sp}\) for \(\ce{PbBr2}\) has a value of \(4 \times 10^{-5}\). Is the solution saturated, oversaturated or unsaturated?
Solutions
- Answer 1.2e-6
Hint...
The equilibrium equation and concentrations x are shown below\(\begin{array}{cccccc}
\ce{CuCl &\rightleftharpoons &Cu+ &+ &Cl- &}\\
&&x &&x &\hspace{10px}(x = \textrm{1.1e-3})
\end{array}\)\(K_{\ce{sp}} = \ce{[Cu+][Cl- ]} = (\textrm{1.1e-3})^2 =\: ?\: \ce M^2\)
If \(\ce{CuCl2}\) is used, you would have \(\ce{CuCl2 \rightleftharpoons Cu^2+ + 2 Cl-}\). - Answer 2.2e-10
Hint...
Let x be the molar solubility, then \(\ce{[Hg2^2+]} = x\); and \(\ce{[I- ]} = 2 x\);\(\begin{array}{ccccc}
\ce{Hg2I2 &\rightleftharpoons &Hg2^2+ &+ &2 I-}\\
x &&x &&2 x
\end{array}\)Molar solubility = \(\ce{[Hg2^2+]}\).
\(\ce{[I- ]} = \ce{2 [Hg2^2+]}\).
\(K_{\ce{sp}} = x\, (2 x)^2 = \textrm{4.5e-29}\); \(x =\: ?\)
- Answer 12.35
Hint...
Let \(\ce{[Ca^2+]} = x\), then \(\ce{[OH- ]} = 2 x\). The equilibrium and concentration are represented below:\(\begin{array}{ccccc}
\ce{Ca(OH)2 &\rightleftharpoons &Ca^2+ &+ &2 OH-}\\
&&x &&2 x
\end{array}\)\(x = \left (\dfrac{\textrm{5.5e-6}}{4} \right )^{1/3}\)
\(\ce{[OH- ]} = 2 x\).
Note the stoichiometry of equilibrium. - Answer unsaturated
Hint...
[0.012] [0.024]2 = 6.9e-6 < 4e-5 (Ksp).
This question deals with the concept of ion product, Qsp.
If \(Q_{\ce{sp}} = \ce{[Pb^2+][Br- ]^2} < K_{\ce{sp}}\) the solution is unsaturated.
Contributors and Attributions
Chung (Peter) Chieh (Professor Emeritus, Chemistry @ University of Waterloo)

