3.2.1: Elementary Reactions

An elementary reaction is a single step reaction with a single transition state and no intermediates.

Introduction

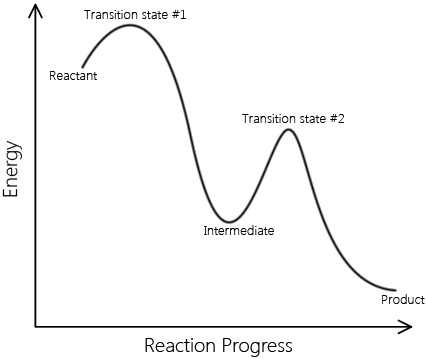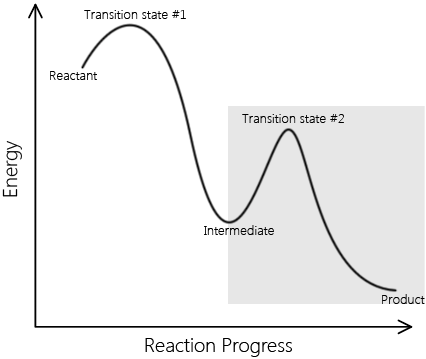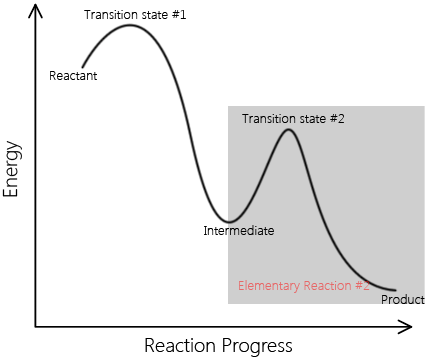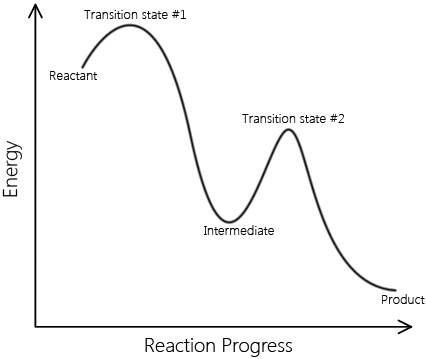
Elementary reactions add up to complex reactions; non-elementary reactions can be described by multiple elementary reaction steps. A set of elementary reactions comprises a reaction mechanism, which predicts the elementary steps involved in a complex reaction. Below are two reaction coordinates of two reactions. One describes an elementary reaction, and the other describes a non-elementary reaction.

Elementary Reaction (one step)	Two Step Reaction
\[ \text{Reactants} \rightarrow \text{Products} \nonumber \] This is a sample reaction coordinate of an elementary reaction. Note that there is one transition state and no intermediate. Elementary steps cannot be broken down into simpler reactions.	\[ \text{Reactants} \rightarrow \text{Intermediates} \rightarrow \text{Products} \nonumber \] This is a sample reaction coordinate of a complex reaction. Note that it involves an intermediate and multiple transition A complex reaction can be explained in terms of elementary reactions.

Types of Elementary Reactions

The molecularity of a reaction refers to the number of reactant particles involved in the reaction. Because there can only be discrete numbers of particles, the molecularity must take an integer value. Molecularity can be described as unimolecular, bimolecular, or termolecular. There are no known elementary reactions involving four or more molecules.¹

Unimolecular Reaction	Bimolecular Reaction	Termolecular Reaction

Unimolecular Reaction

A unimolecular reaction occurs when a molecule rearranges itself to produce one or more products. An example of this is radioactive decay, in which particles are emitted from an atom. Other examples include cis-trans isomerization, thermal decomposition, ring opening, and racemization. The rate at which a substance decomposes is dependent on its concentration. Unimolecular reactions are often first-order reactions as explained by Frederick Alexander Lindemann, which is referred to as the Lindemann mechanism.

Bimolecular Reaction

A bimolecular reaction involves the collision of two particles. Bimolecular reactions are common in organic reactions such as nucleophilic substitution. The rate of reaction depends on the product of the concentrations of both species involved, which makes bimolecular reactions second-order reactions.

Termolecular Reaction

A termolecular reaction requires the collision of three particles at the same place and time. This type of reaction is very uncommon because all three reactants must simultaneously collide with each other, with sufficient energy and correct orientation, to produce a reaction. There are three ways termolecular reactions can react, and all are third order.

Table 1: The three known types of elementary reactions:

Molecularity	Elementary Step	Rate Law	Example
Unimolecular	\(A \rightarrow Products\)	\(rate = k[A]\)	\(N_2O_{4(g)} \rightarrow 2NO_{2(g)}\)
Bimolecular	\(A + A \rightarrow Products\)	\(rate = k[A]^2\)	\(2NOCl \rightarrow 2NO_{(g)} + Cl_{2(g)}\)
	\(A + B \rightarrow Products\)	\(rate = k[A][B]\)	\(CO_{(g)} + NO_{3(g)} \rightarrow NO_{2(g)} + CO_{2(g)}\)
Termolecular	\(A + A +A \rightarrow Products\)	\(rate = k[A]^3\)
	\(A + A + B \rightarrow Products\)	\(rate = k[A]^2[B]\)	\(2NO_{(g)} + O_{2(g)} \rightarrow 2NO_{2(g)}\) ^2
	\(A + B + C \rightarrow Products\)	\(rate = k[A][B][C]\)	\(H + O_{2(g)} + M \rightarrow HO_{2(g)} + M\) ^3

Practice Problems

1. How are non-elementary steps and elementary steps related? 2. Choose the correct statements.

a. An elementary step has 0 intermediates.

b. An elementary step has 1 intermediate.

c. An elementary step has 2 intermediates.

d. An elementary step has 0 transition states.

e. An elementary step has 1 transition state.

f. An elementary step has 2 transition states.

3. Which of the following elementrary reactions is a termolecular reaction?

a. \(A + 2B + C \rightarrow D\)

b. \(A + B + B \rightarrow C\)

c. all of the above

d. \(2A + 2B + 2C \rightarrow 2D\)

e. b and d

f. none of the above

4. Which rate law corresponds to a bimolecular reaction?

a. \(rate = k[A][A]^2\)

b. \(rate = k[A][B]\)

c. all of the above

d. \(rate = k[A]^2\)

e. b and d

f. none of the above

5. Give an example of a reaction with a molecularity of 1/2. 6. True or False: Given species A and B inside a container, instruments detect that three (3) collisions occured before product was formed. That is, we know a reaction occured after detecting three collisions in a box. We can conclude that the reaction is a termolecular reaction (as the reaction could have been produced from A+A+B or A+B+B).

Solutions

1. Non-elementary steps, or complex reactions, are sets of elementary reactions. The addition of elementary steps produces complex, non-elementary reactions.

2. The correct statements are "a" and "e". By definition of elementary reactions they have 0 intermediates because they cannot be broken down. Again by definition of an elementary reaction, a single-step reaction will have 1 transition state. There is no reaction with 0 transition states. Having 2 transition states implies having 1 intermediate, making the reaction non-elementary.

3. "e" is the answer.

"a" is not a termolecular reaction because it involves A + B + B + C, or 4 molecules

"b" is a termolecular reaction because it involves 3 particles: A + B + B

"c" is incorrect because "a" is incorrect

"d" is a termolecular reaction, simplifying to the reaction: \(A + B + C \rightarrow D\), which involves 3 particles (A + B + C)

"e" is the correct answer because "b" and "d" are correct

4. "e" is the answer.

"a" is incorrect because the rate law describes a third-order reaction, which is true for termolecular reactions

"b" is a possible rate law for the bimolecular reaction: \(A + B \rightarrow Products\)

"c" is incorrect because "a" is incorrect

"d" is a possible rate law for the bimolecular reaction: \(A + A \rightarrow Products\)

"e" is the correct answer because "b" and "d" are correct

5. Impossible. The molecularity of a reaction MUST be an integer because there cannot be a "half particle" producing a reaction.

6. False; nothing can be concluded. Although a termolecular reaction requires the collision of three particles, the reverse logic is not necessarily true. That is, having three collisions is not sufficient for a termolecular reaction.

1. For example, particles A + A + B collide with each other at the same place and time. However, particle B was in the wrong orientation, so no reaction occurred. Instead, the two A particles were in the correct orientation and produced a reaction, which is a bimolecular reaction.

2. Consider a second example: two collisions between particles A + A + B occurred, but there was not enough energy to produce a reaction. Instead, a third collision between A and B had the sufficient energy and correct orientation to produce a reaction. Such a reaction is, again, only bimolecular.

3. A last example: particle A collides twice with a wall, and then once with B to produce a reaction. Such a reaction involving three collisions at different places and different time is only a bimolecular reaction.

References

1. Chang, Raymond. "Chemical Kinetics." Physical Chemistry for the Biosciences. Sansalito, CA: University Science, 2005. 325-328. Print.
2. Olbregts, J. (1985), Termolecular reaction of nitrogen monoxide and oxygen: A still unsolved problem. International Journal of Chemical Kinetics, 17: 835–848. doi: 10.1002/kin.550170805.
3. Kerr, James Alistair. "Notes on the Tables." CRC Handbook of bimolecular and termolelucar gas reactions . Boca Raton, Florida: CRC Press, 1987. 2. Print.
4. Baer, Tomas, and William L. Hase. "Introduction." Unimolecular reaction dynamics: theory and experiments. New York: Oxford University Press, 1996. 4-5. Print.

Contributors and Attributions

• Tho Nguyen (UCD), Minh Ngo (UCD)