Stereoisomers: Ring Conformations

Ring Conformations

Although the customary line drawings of simple cycloalkanes are geometrical polygons, the actual shape of these compounds in most cases is very different.

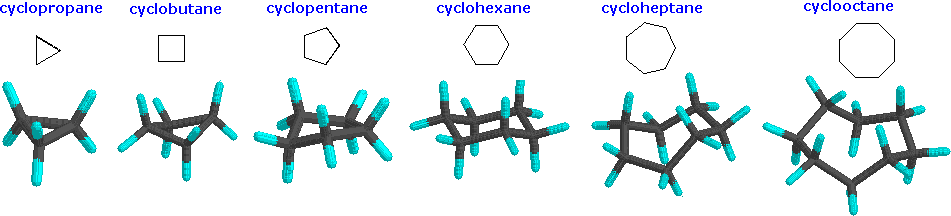
Cyclopropane is necessarily planar (flat), with the carbon atoms at the corners of an equilateral triangle. The 60º bond angles are much smaller than the optimum 109.5º angles of a normal tetrahedral carbon atom, and the resulting angle strain dramatically influences the chemical behavior of this cycloalkane. Cyclopropane also suffers substantial eclipsing strain, since all the carbon-carbon bonds are fully eclipsed. Cyclobutane reduces some bond-eclipsing strain by folding (the out-of-plane dihedral angle is about 25º), but the total eclipsing and angle strain remains high. Cyclopentane has very little angle strain (the angles of a pentagon are 108º), but its eclipsing strain would be large (about 10 kcal/mol) if it remained planar. Consequently, the five-membered ring adopts non-planar puckered conformations whenever possible. Rings larger than cyclopentane would have angle strain if they were planar. However, this strain, together with the eclipsing strain inherent in a planar structure, can be relieved by puckering the ring. Cyclohexane is a good example of a carbocyclic system that virtually eliminates eclipsing and angle strain by adopting non-planar conformations, such as those shown below. Cycloheptane and cyclooctane have greater strain than cyclohexane, in large part due to transannular crowding (steric hindrance by groups on opposite sides of the ring).

Some Conformations of Cyclohexane Rings

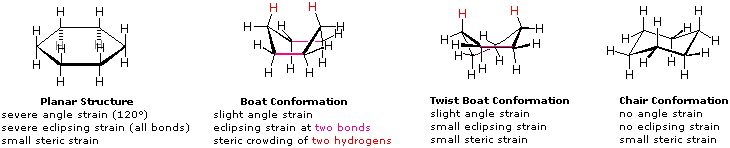
A planar structure for cyclohexane is clearly improbable. The bond angles would necessarily be 120º, 10.5º larger than the ideal tetrahedral angle. Also, every carbon-carbon bond in such a structure would be eclipsed. The resulting angle and eclipsing strains would severely destabilize this structure. If two carbon atoms on opposite sides of the six-membered ring are lifted out of the plane of the ring, much of the angle strain can be eliminated. This boat structure still has two eclipsed bonds (colored magenta in the drawing) and severe steric crowding of two hydrogen atoms on the "bow" and "stern" of the boat. Thissteric crowding is often called steric hindrance. By twisting the boat conformation, the steric hindrance can be partially relieved, but the twist-boat conformer still retains some of the strains that characterize the boat conformer. Finally, by lifting one carbon above the ring plane and the other below the plane, a relatively strain-free chair conformer is formed. This is the predominant structure adopted by molecules of cyclohexane.

An energy diagram for these conformational interconversions is drawn below. The activation energy for the chair-chair conversion is due chiefly to a high energy twist-chair form (TC), in which significant angle and eclipsing strain are present. A facile twist-boat (TB)-boat (B) equilibrium intervenes as one chair conformer (C) changes to the other.

Conformational Energy Profile of Cyclohexane
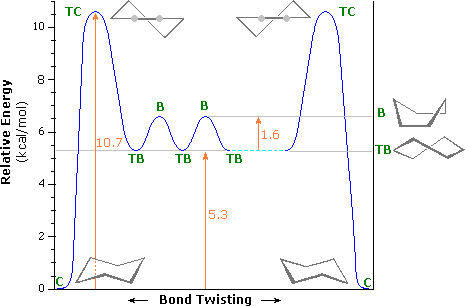		TC = twist chair
		B = boat
		TB = twist boat
		C = chair

These conformations may be examined as interactive models by .

Investigations concerning the conformations of cyclohexane were initiated by H. Sachse (1890) and E. Mohr (1918), but it was not until 1950 that a full treatment of the manifold consequences of interconverting chair conformers and the different orientations of pendent bonds was elucidated by D. H. R. Barton (Nobel Prize 1969 together with O. Hassel). The following discussion presents some of the essential features of this conformational analysis.

On careful examination of a chair conformation of cyclohexane, we find that the twelve hydrogens are not structurally equivalent. Six of them are located about the periphery of the carbon ring, and are termedequatorial. The other six are oriented above and below the approximate plane of the ring (three in each location), and are termed axial because they are aligned parallel to the symmetry axis of the ring. In the stick model shown on the left below, the equatorial hydrogens are colored blue, and the axial hydrogens are red. Since there are two equivalent chair conformations of cyclohexane in rapid equilibrium, all twelve hydrogens have 50% equatorial and 50% axial character.

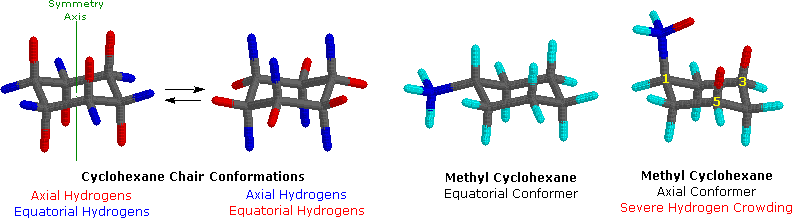
Because axial bonds are parallel to each other, substituents larger than hydrogen generally suffer greater steric crowding when they are oriented axial rather than equatorial. Consequently, substituted cyclohexanes will preferentially adopt conformations in which large substituents assume equatorial orientation. In the two methylcyclohexane conformers shown above, the methyl carbon is colored blue. When the methyl group occupies an axial position it suffers steric crowding by the two axial hydrogens located on the same side of the ring. This crowding or steric hindrance is associated with the red-colored hydrogens in the structure. A careful examination of the axial conformer shows that this steric hindrance is due to two gauche-like orientations of the methyl group with ring carbons #3 and #5. The use of models is particularly helpful in recognizing and evaluating these relationships.

These conformations may be examined as interactive models by

To view an animation of the interconversion of cyclohexane chair conformers

The relative steric hindrance experienced by different substituent groups oriented in an axial versus equatorial location on cyclohexane may be determined by the conformational equilibrium of the compound. The corresponding equilibrium constant is related to the energy difference between the conformers, and collecting such data allows us to evaluate the relative tendency of substituents to exist in an equatorial or axial location. A table of these free energy values (sometimes referred to as A values) may be examined by .

Clearly the apparent "size" of a substituent is influenced by its width and bond length to cyclohexane, as evidenced by the fact that an axial vinyl group is less hindered than ethyl, and iodine slightly less than chlorine.

Contributors

• William Reusch, Professor Emeritus (Michigan State U.), Virtual Textbook of Organic Chemistry