Alkanes Background

This is an introductory page about alkanes, such as methane, ethane, propane, butane and the remainder of the common alkanes. This page addresses their formulae and isomerism, their physical properties, and an introduction to their chemical reactivity.

Molecular Formulas

Alkanes are the simplest family of hydrocarbons - compounds containing carbon and hydrogen only. Alkanes only contain carbon-hydrogen bonds and carbon-carbon single bonds. The formula of any of the alkanes follow the general formula \(C_nH_{2n+2}\) _. The first six alkanes are tabulated below:

Table 1: The first six alkanes are as follows:

name	Formula
methane	CH4
ethane	C2H6
propane	C3H8
butane	C4H10
pentane	C5H12
hexane	C6H14

Isomerism

All of the alkanes containing 4 or more carbon atoms show structural isomerism, meaning that there are two or more different structural formulae that you can draw for each molecular formula.

Example 1: Butane or MethylPropane

C₄H₁₀ could be either of these two different molecules:

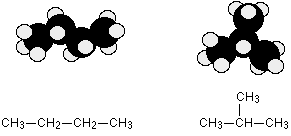
These are named butane and 2-methylpropane, respectively.

Cycloalkanes

Cycloalkanes also only contain carbon-hydrogen bonds and carbon-carbon single bonds, but the carbon atoms are joined in a ring. The smallest cycloalkane is cyclopropane.

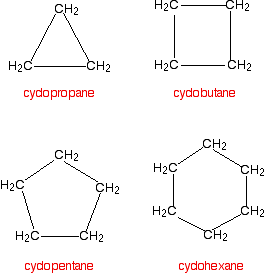
If you count the carbons and the hydrogens, you will see that they no longer adhere to the general formula C_nH_2n+2. By joining the carbon atoms in a ring, two hydrogen atoms are lost. The general formula for a cycloalkane is C_nH_2n and these are non-planar molecules (with the exception of cyclopentane) and exist as "puckered rings".

Example 2: Cyclohexane Conformation

Cyclohexane has a ring structure that looks like this:

This is known as the "chair" form of cyclohexane because of its shape, which vaguely resembles a chair. Cyclohexane also has a boat configuration (not shown).

Physical Properties

Boiling Points

The boiling points shown are for the "straight chain" isomers in which there are more than one (Figure 1). Notice that the first four alkanes are gases at room temperature, and solids do not start to appear until about C₁₇H₃₆.

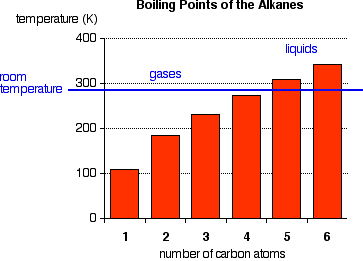
Figure 1:Normal boiling points of first four alkanes

The temperatures cannot be more precise than those given in this chart because each isomer has a different melting and boiling point. By the time you get 17 carbons into an alkane, there are unbelievable numbers of isomers! Cycloalkanes have boiling points that are approximately 10 - 20 K higher than the corresponding straight chain alkane.

There electronegativity difference between carbon and hydrogen (2.1 vs. 1.9) is small; therefore, there is only a slight bond polarity, meaning that the only attractions between one molecule and its neighbors will be Van der Waals dispersion forces. These forces will be very small for a molecule like methane but will increase as the size of the molecules increase. Therefore, the boiling points of the alkanes increase with the molecular size.

Regarding isomers, the more branched the chain, the lower the boiling point tends to be. Van der Waals dispersion forces are smaller for shorter molecules and only operate over very short distances between one molecule and its neighbors. It is more difficult for short, bulky molecules (with substantial amounts of branching) to lie close together (compact) compared with long, thin molecules.

Example 3

The boiling points of the three isomers of C₅H₁₂ are as follows:

• pentane (309.2 K)
• 2-methylbutane (301.0 K)
• 2,2-dimethylpropane (282.6 K)

The slightly higher boiling points for the cycloalkanes are presumably because the molecules can get closer together because the ring structure makes them tidier and less "wriggly"!

Solubility

Alkanes (both normal and cycloalkanes) are virtually insoluble in water but dissolve in organic solvents. The liquid alkanes are good solvents for many other covalent compounds. When a molecular substance dissolves in water, the following must occur:

• breaking of the intermolecular forces within the substance. In the case of the alkanes, these are the Van der Waals dispersion forces.
• breaking of the intermolecular forces in the water so that the substance can fit between the water molecules. In water, the primary intermolecular attractions are hydrogen bonds.

Breaking either of these attractions requires energy, although the amount of energy required to break the Van der Waals dispersion forces in a compound, such as methane, is relatively negligible; this is not true of the hydrogen bonds in water.

To simplify, a substance will dissolve if sufficient energy is released when the new bonds are formed between the substance and the water to make up for the energy required to break the original attractions. The only new attractions between the alkane and the water molecules are the Van der Waals forces. These forces to do not release a sufficient amount of energy to compensate for the energy required to break the hydrogen bonds in water. Therefore, the alkane does not dissolve.

Solubility in organic solvents

In most organic solvents, the primary forces of attraction between the solvent molecules are the Van der Waals forces composed of either dispersion forces or dipole-dipole attractions. Therefore, when an alkane dissolves in an organic solvent, the Van der Waals forces are broken and are replaced by new Van der Waals forces. The two processes more or less cancel each other out energetically; thus, there is no barrier to solubility.

Chemical Reactivity

Alkanes contain strong carbon-carbon single bonds and strong carbon-hydrogen bonds. The carbon-hydrogen bonds are only very slightly polar. Therefore, there is no portion of the molecule that carries any significant amount of positive or negative charge, which is required for other molecules to be attracted to it. For example, many organic reactions start because an ion or a polar molecule is attracted to a portion of an organic molecule, which carries some positive or negative charge. This attraction does not occur with alkanes because alkane molecules do not have this separation of charge. The net effect is that alkanes have a fairly restricted set of reactions, including the following:

• burn them - destroying the entire molecule;
• react them with some of the halogens, breaking the carbon-hydrogen bonds;
• crack them, breaking carbon-carbon bonds.

These reactions are covered in separate pages.

Cycloalkanes are very similar to the alkanes in reactivity, except for the very small cycloalkanes, especially cyclopropane. Cyclopropane is much more reactive than what is expected because of the bond angles in the ring. Normally, when carbon forms four single bonds, the bond angles are approximately 109.5°.

Example 4: Cyclopropane

In cyclopropane, the bond angles are 60°.

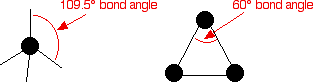
With the electron pairs this close together, there is a significant amount of repulsion between the bonding pairs joining the carbon atoms, making the bonds easier to break.

Conformational Analysis of Alkanes

A conformational analysis is a study of the energetics of different spatial arrangements of atoms relative to rotations about bonds. Conformational analyses are assisted greatly by a representation of molecules in a manner different to skeletal structures. A representation of a molecule in which the atoms and bonds are viewed along the axis about which rotation occurs is called a Newman projection (Figure 2).

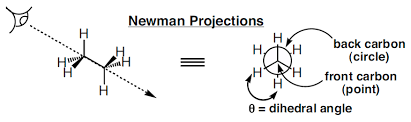
Figure 2: Newman projection of ethane

In a Newman projection, the molecule is viewed along an axis containing two atoms bonded to each other and the bond between them, about which the molecule can rotate. In a Newman projection, the "substituents" of each atom composing the bond, be they hydrogens or functional groups, can then be viewed both in front of and behind the carbon-carbon bond. Specifically, one can observe the angle between a substituent on the front atom and a substituent on the back atom in the Newman projection, which is called the dihedral angle or torsion angle.

In ethane specifically, we can imagine two possible "extreme" conformations. In one case, the dihedral angle is 0° and the hydrogens on the first carbon line up with or eclipse the hydrogens on the second carbon. When the dihedral angle is 0° and the hydrogens line up perfectly, ethane has adopted the eclipsed conformation (Figure 3). The other extreme occurs when the hydrogens on the first carbon are as far away as possible from those on the second carbon; this occurs at a dihedral angle of 60° and is called the staggered conformation (Figure 3).

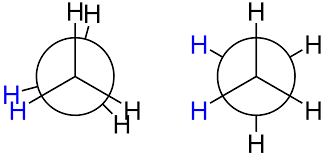
Figure 3: Conformations of ethane - staggered and eclipsed

The staggered conformation of ethane is a more stable, lower energy conformation than the eclipsed conformation because the eclipsed conformation involves unfavorable interactions between hydrogen atoms. Specifically, the negatively charged electrons in the bonds repel each other most when the bonds line up. Thus, ethane spends most of its time in the more stable staggered conformation.

Conformational analysis of butane

In butane, two of the substituents, one on each carbon atom being viewed, is a methyl group. Methyl groups are much larger than hydrogen atoms. Thus, when eclipsed conformations occur in butane, the interactions are especially unfavorable. There are four possible "extreme" conformations of butane: 1) Fully eclipsed, when the methyl groups eclipse each other; 2) Gauche, when the methyl groups are staggered but next to each other; 3) Eclipsed, when the methyl groups eclipse hydrogen atoms; and 4) Anti, when the methyl groups are staggered and as far away from each other as possible (Figure 4).

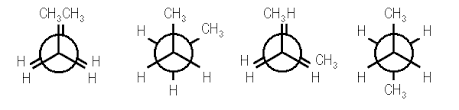
Figure 4: Conformations of butane: fully eclipsed, gauche, eclipsed, and anti

The fully eclipsed conformation is clearly the highest in energy and least favorable since the largest groups are interacting directly with each other. As the molecule rotates, it adopts the relatively stable gauche conformation. As it continues to rotate, it encounters less favorable eclipsed conformation in which a methyl group eclipses a hydrogen. As rotation continues, the molecule comes to the anti conformation, which is the most stable since the substituents are staggered and the methyl groups are as far away from each other as possible. An energy diagram is a graph which represents the energy of a molecule as a function of some changing parameter. An energy diagram can be made as a function of dihedral angle for butane (Figure 5).

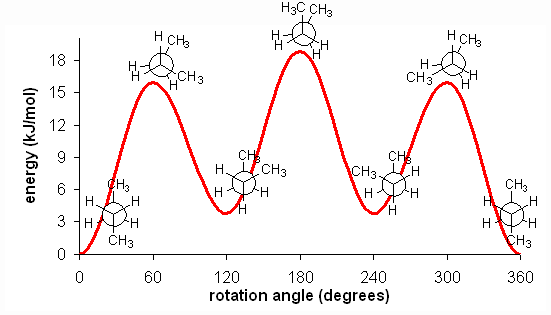
Figure 5: Energy diagram for conformations of butane as a function of dihedral angle

Clearly, the anti and gauche conformations are significantly more stable than the eclipsed and fully eclipsed conformations. Butane spends most of its time in the anti and gauche conformations.

There is one final, very important point. At room temperature, approximately 84 kJ/mol of thermal energy is available to molecules. Thus, if the barrier to a rotation is less than 84 kJ/mol, the molecule will rotate. In ethane and butane, the barriers to rotation are significantly less than 84 kJ/mol. Therefore, even though the eclipsed conformations are unfavorable, the molecules are able to adopt them. In reality, since these conformations are not as stable, the molecules will quickly pass through them at room temperature and return a staggered conformation. Molecules are constantly converting between different staggered conformations all the time, quickly passing through eclipsed conformations in between. Thus, in alkanes, no single "true" conformation exists all the time; the molecule instead constantly converts between conformations, spending more time in those that are more stable. This constant conversion lies in stark contract to alkenes, which adopt the cis- or trans- (E- or Z-) conformations and retain them at room temperature; they do not interconvert because the barrier to rotation is too high.

Contributors

• Jim Clark (Chemguide.co.uk)

• Jonathan Mooney (McGill University)