5.01: Symmetry Elements
- Page ID
- 210949
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Symmetry elements of the molecule are geometric entities: an imaginary point, axis or plane in space, which symmetry operations: rotation, reflection or inversion, are performed.[1],[2] Their recognition leads to the application of symmetry to molecular properties and can also be used to predict or explain many of a molecule’s chemical properties. Symmetry elements and symmetry operations are two fundamental concepts in group theory, which is the mathematical description of symmetry properties that describe the structure, bonding, and spectroscopy of molecules.
Point Symmetry Operations
Point symmetry of a molecule results when there exists at least one point in space that remains indistinguishable from the original molecule after any symmetry operation is applied. In other words, a rotation, reflection or inversion operations are called symmetry operations if, and only if, the newly arranged molecule is indistinguishable from the original arrangement. There are five kinds of point of symmetry elements that a molecule can possess, thus, there are also five kinds of point of symmetry operations. All symmetry elements in a molecule must share at least one point in common and this point occurs at the center of the molecule.
Identity, E
Identity operation comes from the German ‘Einheit’ meaning unity. This symmetry element means no change. All molecules have this element.
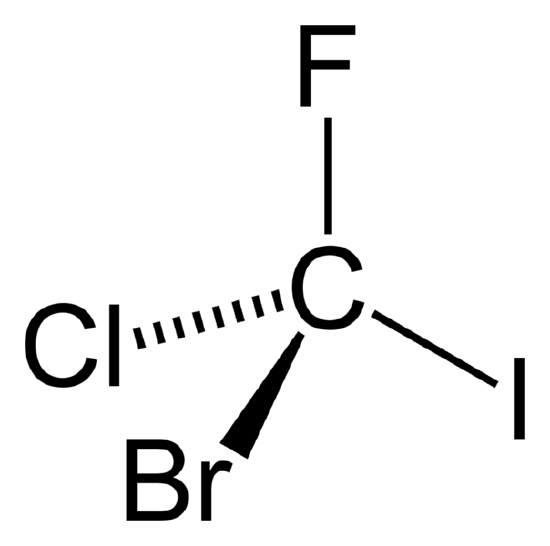
Figure \(\PageIndex{1}\) CFClBrI. A chiral molecule possesses no symmetry but identity operation, E.
Proper Rotation, Cn
Proper rotation operates with respect to an axis called a symmetry axis (also known as n-fold rotational axis). An axis around which a rotation by 360°/n (or 2π/n) results in an identical molecule before and after the rotation. The axis with the highest n is called the principal axis.
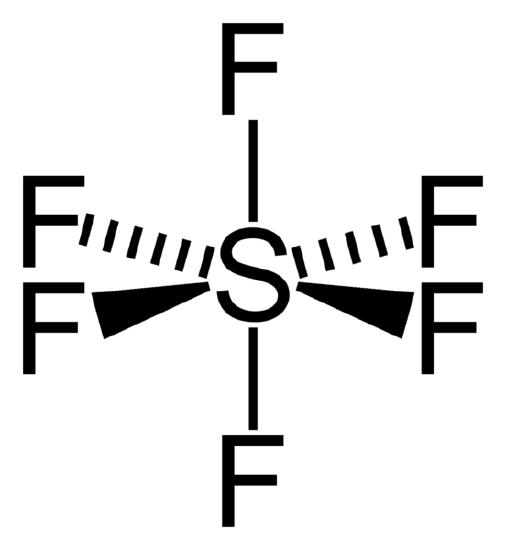
Figure \(\PageIndex{2}\) Octahedral structure of SF6. Proper rotations of SF6 are 5C2, 4C3 and 3C4 and we call C4 the principal axis of SF6.
In general, a molecule contains nCn operations such that {Cn1, Cn2, Cn3,…, Cnn-1, Cnn} where Cnn = E. For example, if there exists C5 axis then there exists 5C5 (2C51, 2C52, C55) operations:
- C51 = C54 since the operation results indistinguishable molecule in clockwise and counter-clockwise, respectively.
- C52 = C53 since the operation results indistinguishable molecule in clockwise and counter-clockwise, respectively.
- C55 = E
Reflection, σ
Reflection operates with respect to a plane called a plane of symmetry (also known as a mirror plane). There exist three types of mirror planes:
- σh – a horizontal mirror plane of a molecule is perpendicular to the primary axis of a molecule.
- σv – a vertical mirror plane of a molecule includes the primary axis of a molecule and passes through the bonds (atoms).
- σd – a dihedral (also known as a diagonal mirror plane) of a molecule includes the primary axis of a molecule while bisecting the angle between two C2 axes that are perpendicular to it. Therefore, ơd does not pass through the bonds (atoms).
NOTE: σd is a special case of a σv.
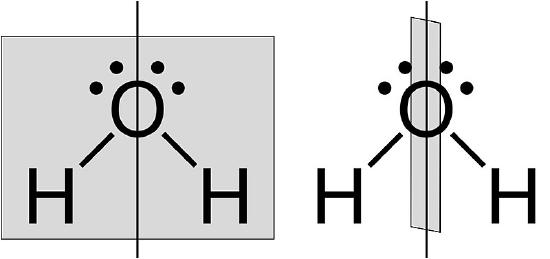
Figure \(\PageIndex{3}\) Bent structure of H2O. The water molecule has two σv along C2 axis and no σh.
Inversion, i
Inversion operates with respect to a point called a center of symmetry (also known as an inversion center). It gives the same result to rotating a molecule around C2 axis then reflecting it with respect to a mirror plane that is perpendicular to C2. For example, SF6 in figure \(\PageIndex{2}\) has an inversion point at the center S.
Improper Rotation, Sn
Improper rotation operates with respect to an axis called rotation-reflection axis. In other words, it is a combination operation of a rotation about an axis by 360°/n (or 2π/n) followed by reflection in a plane perpendicular to the rotation axis.
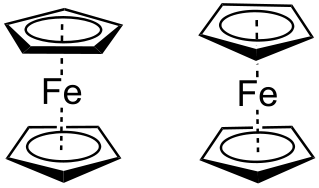
Figure \(\PageIndex{4}\) Staggered ferrocene (left) has an S10 operation while eclipsed ferrocene (right) has an S5 operation.
2. Point groups
The complete collection of symmetry elements of a molecule forms the basis of a mathematical group, and the collection of symmetry operations that are interrelated to each other via certain kind of rules is known as a point group:
- Closure – if any two symmetry operations are in the same group then their product, resulting in another operation, will also be in the same group:
If A∈G and B∈G, then (A∩B)∈G
- Associativity – the law of associativity applies to all symmetry operations:
(AB)C=A(BC)
- Identity – there exists an operation that commutes with other operations (identity, E) and leaves them unchanged:
If A∈G and E∈G, then AE=EA=A
- Inverses – for every symmetry operation in the group, there exists an inverse operation that their product results identity:
If A∈G, then there exists A-1∈G such that AA-1=A-1A=E
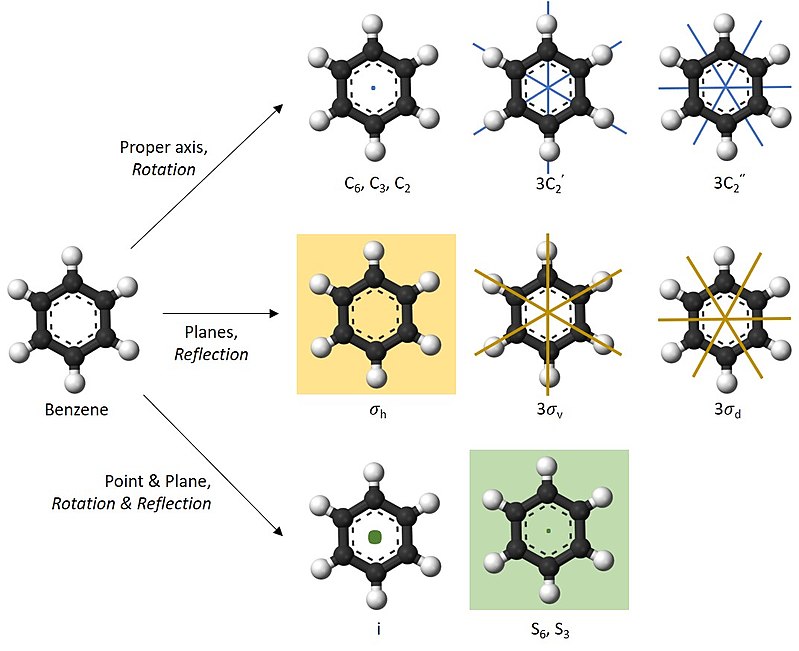
Figure \(\PageIndex{5}\) Benzene is one of the molecules that possess various symmetry elements and symmetry operations.
For more about mathematical representation of symmetry properties, see also:
- Molecular Point Group (1.2)
- Matrices (1.3)
- Representations (1.4)
References
[1] Pfenning, Brian W. (2015). Principles of Inorganic Chemistry. Hoboken: John Wiley & Sons, Inc.. pp. 195.
[2] https://www-e.openu.ac.il/symmetry/symmetry-tutorial.html

