Transformation under Rotation
- Page ID
- 15743
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)We consider transforming between two coordinate systems labeled x, y, z and X, Y, Z. Typically we are concerned with the molecular coordinate system (x,y,z) and the laboratory coordinate system (X,Y,Z). The three Euler angles \(\phi\), \(\theta\), and \(\chi\) shown in the Figure 1 are used to make the transformation between the two coordinate systems.
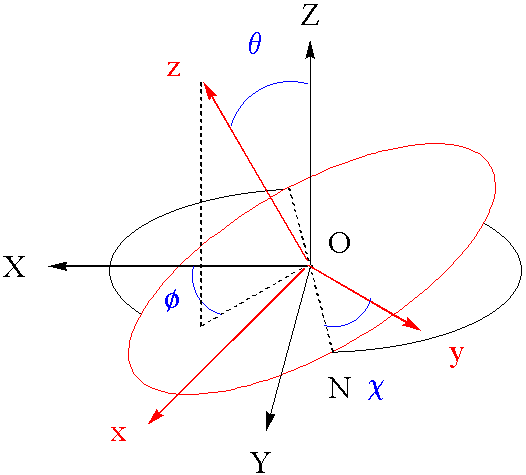
Figure 1: Definition of Reference systems
The angles \(\phi\) and \(\theta\) are spherical polar coordinates where \(\theta\) measures the angle from the Z axis to the z axis and \(\phi\) measures the angle from the X axis to the projection of the z axis on the XY plane. The angle c measures the angle from the line of nodes N, defined to be the intersection of the XY and xy planes, to the y axis. Thus c is an azimuthal angles about the z axis just \(\phi\) is an azimuthal angle about the Z axis. Note that the line of nodes ON is perpendicular to both the z and Z axes.
The Euler angles \(\phi\), \(\theta\), and \(\chi\) should be regarded as defining a prescription whereby the XYZ frame (the space-fixed frame) may be made to coincide with the xyz frame (the body-fixed frame) by three successive rotations:
- A counterclockwise rotation \(\phi\) about Z, the vertical axis. This carries the Y axis into the line of nodes N.
- A counterclockwise rotation \(\theta\) about the line of nodes N. The carries the Z axis into the z axis (the figure axis of the body).
- A counterclockwise rotation c about z, the figure axis. This carries the line of nodes N into the y axis.
The above prescription may be expressed mathematically as

This is not a very useful expression since it makes use of rotations in both the \(\phi\) and g coordinate frames. We show that R(f,q,c) is equivalent to first a rotation c about the Z axis, then a rotation \(\theta\) about the Y axis and finally a rotation \(\phi\) about the same Z axis:

To prove this we make use of the unitary rotation transformation. In general U carries an operator \(\theta\) into UQU-1. Thus, exp(-iqJN) is the transform of exp(-iqJY) under the rotation exp(-ifJZ):

Similarly, exp(-icJz) is the transform of exp(-icJZ) under the previous rotation, which carried Z into z:

We can always use the identity

Substitution of these three equations into our initial equation for the transformation between the two coordinate frames results in the final equation (II).
These equations show that the three Euler angle rotations may all be carried out in the same coordinate system if the order of the rotations is reversed.
The direction cosine matrix elements
Let r be an arbitrary vector having the Cartesian components rF = (rX, rY, rZ) in the space-fixed (laboratory) frame and the Cartesian components rg = (rx, ry, rz) in the the body-fixed (molecular) frame. These two equivalent descriptions of the vector r are related by a unitary transformation \(\phi\) that is conceniently parameterized by the Euler angles f, q, and c:

We call FFg the direction cosine matrix. It is the matrix that transforms from coordinate system g to coordinate system F. There is a corresponding direction cosine matrix from \(\phi\) to g.

The unitary transformation \(\phi\) is conveniently expressed as three Euler angle rotations:

where \(\phi\) is a rotation about the original Z axis, \(\theta\) is a rotation about the new y axis that coincides with the line of nodes N, and c is a rotation about the final z axis. These rotations of the coordinate system axes are shown below. First, we consider the rotation about the laboratory Z axis by an angle f.
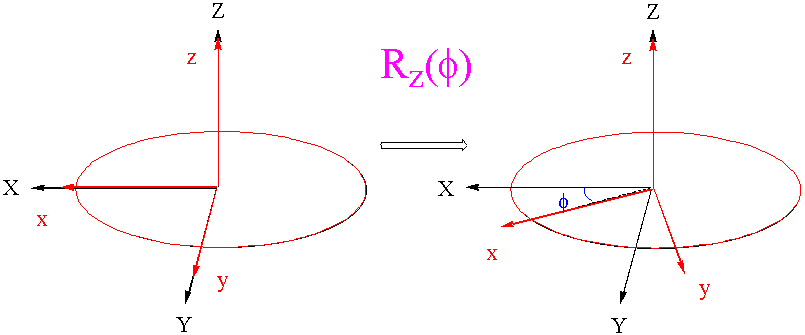
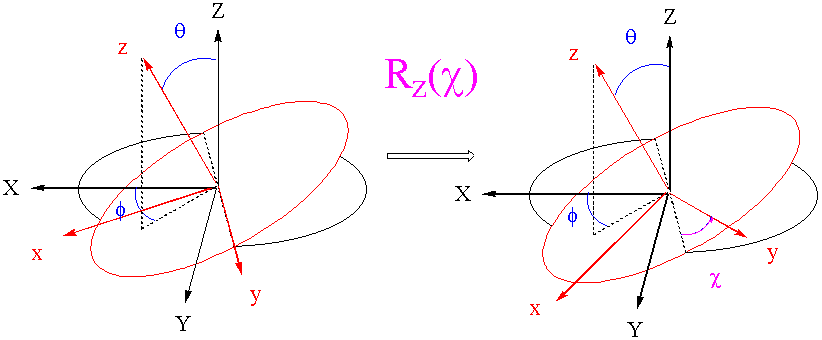
This is followed by a rotation about the new y axis which coincides with the line of nodes. The rotation by \(\theta\) is shown below.

Finally, a rotation about the new z axis by angle c completes the transformation.
Mathematically the rotations can be expressed as matrix transformations. Step 1 involves the rotation about f.

Step 2 involves the rotation about q.

Step 3 involves the rotation about c.

The direction cosine matrix is obtained from the product of these transformations. That is

This can be written explicitly as

Upon matrix multiplication we obtain

where c and s represent cosine and sine, respectively. Because \(\phi\) is a unitary transformation and the elements are real we have that F-1gF = FFg. Thus,

The elements appearing the 3x3 matrices are the cosines of the angles between the various pairs of axes, that is the direction cosines of FgF and FFg, respectively. They have the property that

where indices \(\phi\) and g denote the row and column, respectively. These equations are simply the orthonormality relations of a unitary matrix.

