5.4: Stereogenic Centers
- Page ID
- 30358
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A consideration of the chirality of molecular configurations explains the curious stereoisomerism observed for lactic acid, carvone and a multitude of other organic compounds. Tetravalent carbons have a tetrahedral configuration. If all four substituent groups are the same, as in methane or tetrachloromethane, the configuration is that of a highly symmetric "regular tetrahedron". A regular tetrahedron several planes of symmetry and is achiral.
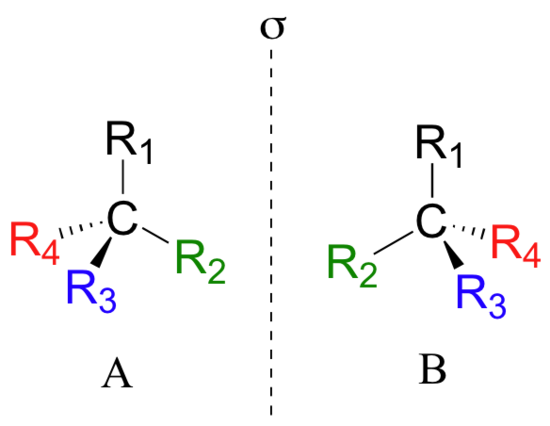
A carbon atom that is bonded to four different atoms or groups loses all symmetry, and is often referred to as an asymmetric carbon. The configuration of such a molecular unit is chiral, and the structure may exist in either a right-handed configuration or a left-handed configuration (one the mirror image of the other). This type of configurational stereoisomerism is termed enantiomorphism, and the non-identical, mirror-image pair of stereoisomers that result are called enantiomers. In the general figure below, A and B are nonsuperposable mirror images of one another, and thus are a pair of enantiomers.
The structural formulas of lactic acid and carvone are drawn on the right with the asymmetric carbon colored red.
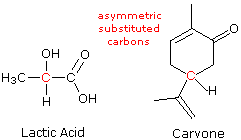
Consequently, we find that these compounds exist as pairs of enantiomers. The presence of a single asymmetrically substituted carbon atom in a molecule is sufficient to render the whole configuration chiral, and modern terminology refers to such groupings as chiral centers. Most of the chiral centers we shall discuss are asymmetric carbon atoms, but it should be recognized that other tetrahedral or pyramidal atoms may become chiral centers if appropriately substituted. When more than one chiral center is present in a molecular structure, care must be taken to analyze their relationship before concluding that a specific molecular configuration is chiral or achiral. This aspect of stereoisomerism will be treated later.
A useful first step in examining structural formulas to determine whether stereoisomers may exist is to identify all stereogenic elements. A stereogenic element is a center, axis or plane that is a focus of stereoisomerism, such that an interchange of two groups attached to this feature leads to a stereoisomer. Stereogenic elements may be chiral or achiral. An asymmetric carbon is often a chiral stereogenic center, since interchanging any two substituent groups converts one enantiomer to the other. Alkenes having two different groups on each double bond carbon constitute an achiral stereogenic element, since interchanging substituents at one of the carbons changes the cis/trans configuration of the double bond.
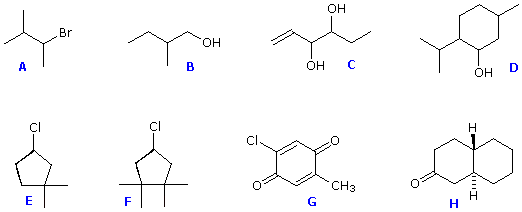
- Show Stereogenci Centers
-
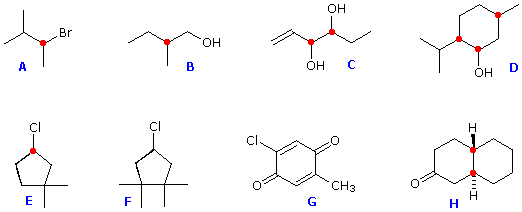
Some of the structures in the figure above are chiral and some are achiral. First, try to identify all chiral stereogenic centers. Formulas having no chiral centers are necessarily achiral. Formulas having one chiral center are always chiral; and if two or more chiral centers are present in a given structure it is likely to be chiral, but in special cases, to be discussed later, may be achiral.
Structures F and G are achiral. The former has a plane of symmetry passing through the chlorine atom and bisecting the opposite carbon-carbon bond. The similar structure of compound E does not have such a symmetry plane, and the carbon bonded to the chlorine is a chiral center (the two ring segments connecting this carbon are not identical). Structure G is essentially flat. All the carbons except that of the methyl group are sp2 hybridized, and therefore trigonal-planar in configuration. Compounds C, D & H have more than one chiral center, and are also chiral. Remember, all chiral structures may exist as a pair of enantiomers. Other configurational stereoisomers are possible if more than one stereogenic center is present in a structure.
In the 1960’s, a drug called thalidomide was widely prescribed in the Western Europe to alleviate morning sickness in pregnant women.
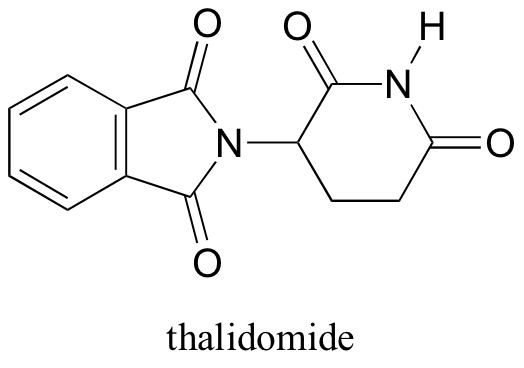
Thalidomide had previously been used in other countries as an antidepressant, and was believed to be safe and effective for both purposes. The drug was not approved for use in the U.S.A. It was not long, however, before doctors realized that something had gone horribly wrong: many babies born to women who had taken thalidomide during pregnancy suffered from severe birth defects.
Researchers later realized the that problem lay in the fact that thalidomide was being provided as a mixture of two different isomeric forms.
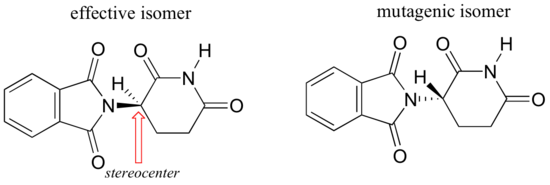
One of the isomers is an effective medication, the other caused the side effects. Both isomeric forms have the same molecular formula and the same atom-to-atom connectivity, so they are not constitutional isomers. Where they differ is in the arrangement in three-dimensional space about one tetrahedral, sp3-hybridized carbon. These two forms of thalidomide are stereoisomers.
Note that the carbon in question has four different substituents (two of these just happen to be connected by a ring structure). Tetrahedral carbons with four different substituent groups are called stereocenters.
Locate all of the carbon stereocenters in the molecules below.
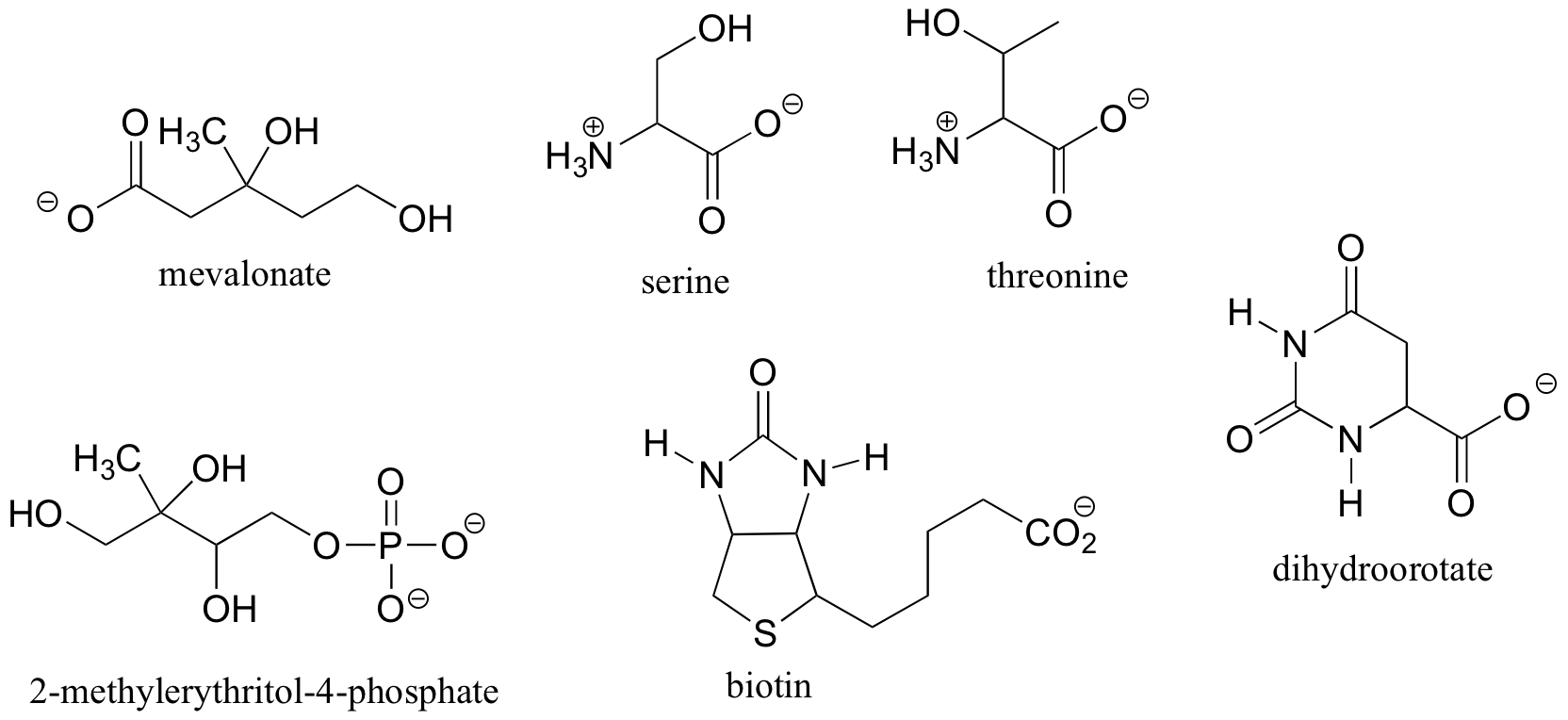
If you look carefully at the figure above, you will notice that molecule A and molecule B are mirror images of each other (the line labeled 's' represents a mirror plane). Furthermore, they are not superimposable: if we pick up molecule A, flip it around, and place it next to molecule B, we see that the two structures cannot be superimposed on each other. They are different molecules!
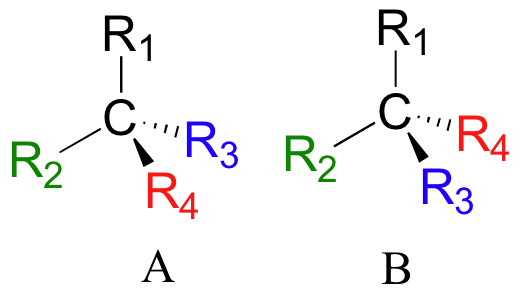
If you make models of the two stereoisomers of thalidomide and do the same thing, you will see that they too are mirror images, and cannot be superimposed (it well help to look at a color version of the figure below).
Thalidomide is a chiral molecule. Something is considered to be chiral if it cannot be superimposed on its own mirror image – in other words, if it is asymmetric (lacking in symmetry). The term ‘chiral’ is derived from the Greek word for ‘handedness’ – ie. right-handedness or left-handedness. Your hands are chiral: your right hand is a mirror image of your left hand, but if you place one hand on top of the other, both palms down, you see that they are not superimposable.
A pair of stereoisomers that are non-superimposable mirror images of one another are considered to have a specific type of stereoisomeric relationship – they are a pair of enantiomers. Thalidomide exists as a pair of enantiomers. On the macro level, your left and right hands are also a pair of enantiomers.
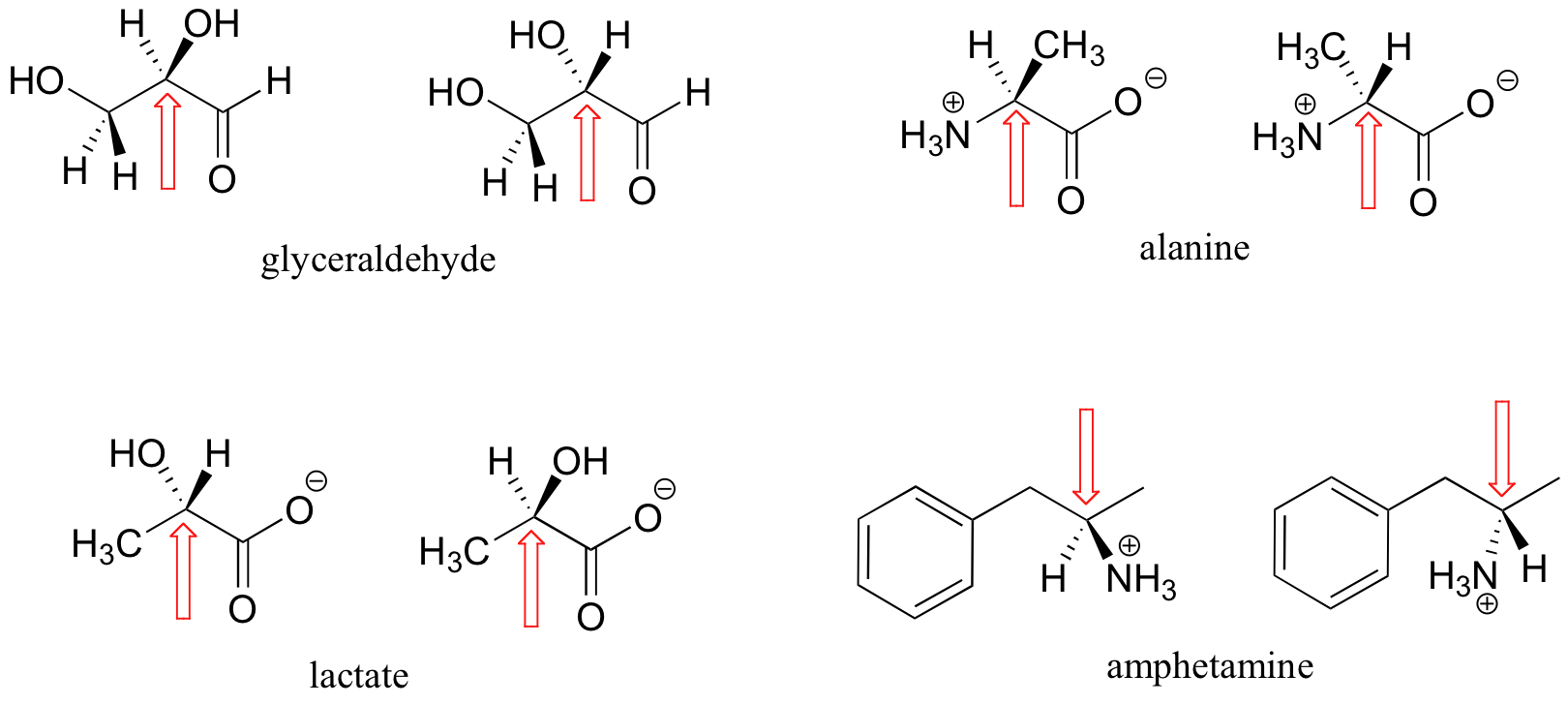
Here are some more examples of chiral molecules that exist as pairs of enantiomers. In each of these examples, there is a single stereocenter, indicated with an arrow. (Many molecules have more than one stereocenter, but we will get to that that a little later!)
Here are some examples of molecules that are achiral (not chiral). Notice that none of these molecules has a stereocenter.
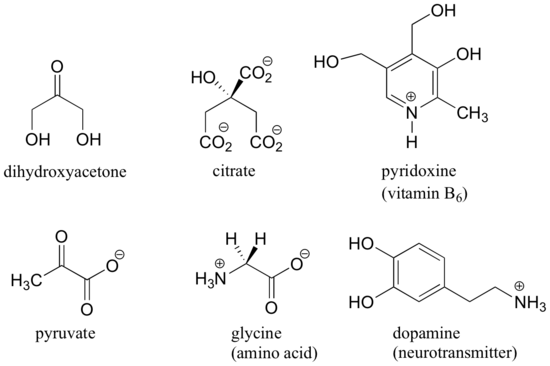
It is difficult to illustrate on the two dimensional page, but you will see if you build models of these achiral molecules that, in each case, there is at least one plane of symmetry, where one side of the plane is the mirror image of the other. Chirality is tied conceptually to the idea of asymmetry, and any molecule that has a plane of symmetry cannot be chiral. When looking for a plane of symmetry, however, we must consider all possible conformations that a molecule could adopt. Even a very simple molecule like ethane, for example, is asymmetric in many of its countless potential conformations – but it has obvious symmetry in both the eclipsed and staggered conformations, and for this reason it is achiral.
Looking for planes of symmetry in a molecule is useful, but often difficult in practice. In most cases, the easiest way to decide whether a molecule is chiral or achiral is to look for one or more stereocenters - with a few rare exceptions (see section 3.7B), the general rule is that molecules with at least one stereocenter are chiral, and molecules with no stereocenters are achiral. Carbon stereocenters are also referred to quite frequently as chiral carbons.
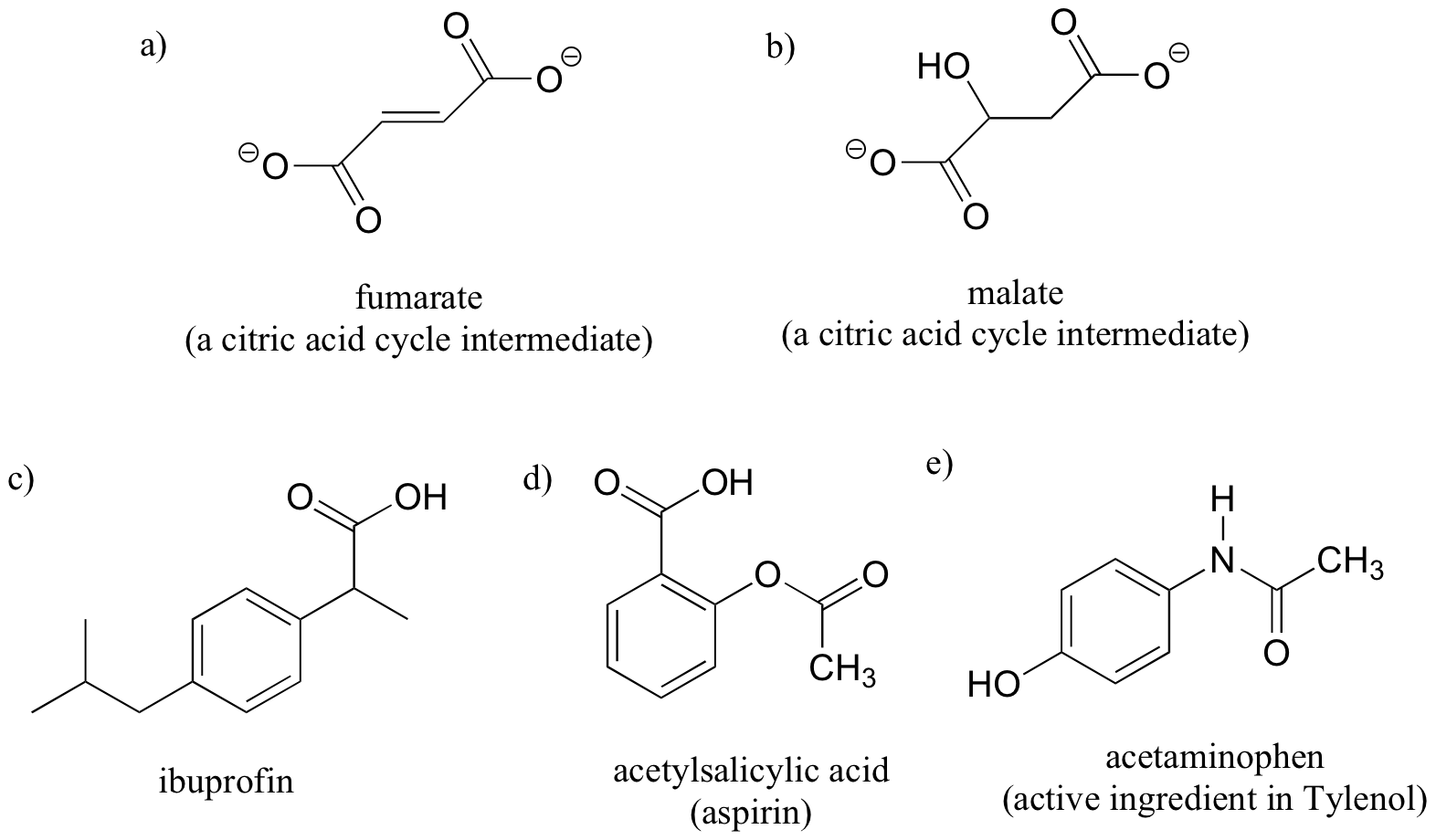
When evaluating a molecule for chirality, it is important to recognize that the question of whether or not the dashed/solid wedge drawing convention is used is irrelevant. Chiral molecules are sometimes drawn without using wedges (although obviously this means that stereochemical information is being omitted). Conversely, wedges may be used on carbons that are not stereocenters – look, for example, at the drawings of glycine and citrate in the figure above. Just because you see dashed and solid wedges in a structure, do not automatically assume that you are looking at a stereocenter.
Other elements in addition to carbon can be stereocenters. The phosphorus center of phosphate ion and organic phosphate esters, for example, is tetrahedral, and thus is potentially a stereocenter.

We will see in chapter 10 how researchers, in order to investigate the stereochemistry of reactions at the phosphate center, incorporated sulfur and/or 17O and 18O isotopes of oxygen (the ‘normal’ isotope is 16O) to create chiral phosphate groups. Phosphate triesters are chiral if the three substituent groups are different.
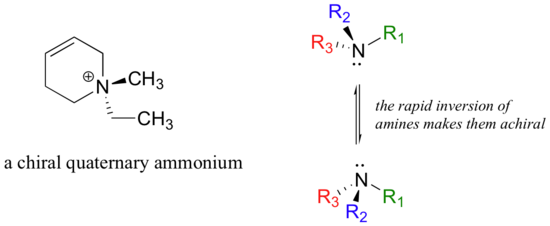
Asymmetric quaternary ammonium groups are also chiral. Amines, however, are not chiral, because they rapidly invert, or turn ‘inside out’, at room temperature.