8.1: Electronic Structure
- Page ID
- 98633
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Skills to Develop
- To understand the basics of electron shielding and penetration
For an atom or an ion with only a single electron, we can calculate the potential energy by considering only the electrostatic attraction between the positively charged nucleus and the negatively charged electron. When more than one electron is present, however, the total energy of the atom or the ion depends not only on attractive electron-nucleus interactions but also on repulsive electron-electron interactions. When there are two electrons, the repulsive interactions depend on the positions of both electrons at a given instant, but because we cannot specify the exact positions of the electrons, it is impossible to exactly calculate the repulsive interactions. Consequently, we must use approximate methods to deal with the effect of electron-electron repulsions on orbital energies. These effects are the underlying basis for the periodic trends in elemental properties that we will explore in this chapter.
Electron Shielding and Effective Nuclear Charge
If an electron is far from the nucleus (i.e., if the distance \(r\) between the nucleus and the electron is large), then at any given moment, many of the other electrons will be between that electron and the nucleus (Figure \(\PageIndex{1}\)). Hence the electrons will cancel a portion of the positive charge of the nucleus and thereby decrease the attractive interaction between it and the electron farther away. As a result, the electron farther away experiences an effective nuclear charge (\(Z_{eff}\)) that is less than the actual nuclear charge \(Z\). This effect is called electron shielding.

Figure \(\PageIndex{1}\): This image shows how inner electrons can shield outer electrons from the nuclear charge. Image used with permission (CC BY-SA 3.0; from NikNaks).
Shielding
Shielding refers to the core electrons repelling the outer electrons, which lowers the effective charge of the nucleus on the outer electrons. Hence, the nucleus has "less grip" on the outer electrons insofar as it is shielded from them.
As the distance between an electron and the nucleus approaches infinity, \(Z_{eff}\) approaches a value of 1 because all the other (\(Z − 1\)) electrons in the neutral atom are, on the average, between it and the nucleus. If, on the other hand, an electron is very close to the nucleus, then at any given moment most of the other electrons are farther from the nucleus and do not shield the nuclear charge. At \(r ≈ 0\), the positive charge experienced by an electron is approximately the full nuclear charge, or \(Z_{eff} ≈ Z\). At intermediate values of \(r\), the effective nuclear charge is somewhere between 1 and \(Z\):
\[1 ≤ Z_{eff} ≤ Z.\]
Notice that \(Z_{eff} = Z\) only for hydrogen. Only for helium are \(Z_{eff}\) and \(Z\) comparable in magnitude − for most atoms, \(Z_{eff}\) for the valence (outermost) electrons is significantly less than \(Z\) (Figure \(\PageIndex{2}\)). In general, the effective nuclear charge of an atom increases as the number of protons in an atom increases, as long as the valence electrons occupy the same shell (Figure \(\PageIndex{2}\)). Therefore as we go from left to right on the periodic table the effective nuclear charge of an atom increases in strength and holds the outer electrons closer and tighter to the nucleus.

Figure \(\PageIndex{2}\): Relationship between the Effective Nuclear Charge Zeff and the Atomic Number Z for the Outer Electrons of the Elements of the First Three Rows of the Periodic Table. Except for hydrogen, (\(Z_{eff}\) is always less than \(Z\), and (\(Z_{eff}\) increases from left to right as you go across a row.
Example \(\PageIndex{1}\): Fluorine, Neon, and Sodium
Rank the effective attraction \(Z_{eff}\) experienced by the valence electrons in the three isoelectronic species: the fluorine anion, the neutral neon atom, and sodium cation.
Solution
Each species has 10 electrons, and the number of nonvalence electrons is 2 (10 total electrons - 8 valence), but the effective nuclear charge varies because each has a different atomic number \(A\). According to the general principle, the more protons in the nucleus, the higher the effective nuclear charge, as long as the valence electrons are in the same shell (in this case, the n=2 shell).
The charge \(Z\) of the nucleus of a fluorine atom is 9, but the valence electrons are screened appreciably by the core electrons (four electrons from the 1s and 2s orbitals) and partially by the 7 electrons in the 2p orbitals. The same holds true for neon, but with \(Z\) = 10, and the sodium cation, but with \(Z\) = 11.
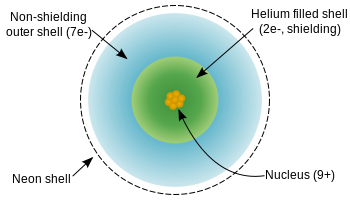
Diagram of a fluorine atom showing the extent of effective nuclear charge. Image used with permission (CC BY-SA- 3.0; from NikNaks).
The sodium cation, with the highest nuclear charge, also has the greatest effective nuclear charge. \(Z_{eff}\) : Na+ > Ne > F-. This also suggests that Na+ has the smallest size among these species and that is correct.
Exercise \(\PageIndex{1}\): Sodium Species
Rank the effective attraction \(Z_{eff}\) experienced by the valence electrons in the sodium anion, the neutral sodium atom, and sodium cation.
- Answer
-
In this case, all three species have the same nuclear charge, but going from the cation to the anion, electrons are added, which would increase the shielding of the other electrons. More shielding would mean a lower effective nuclear charge in the species with more electrons.
\(Z_{eff}\) : Na+ > Na > Na-
Electron Penetration
The actual \(Z_{eff}\) experienced by an electron in a given orbital depends not only on the spatial distribution of the electron in that orbital but also on the distribution of all the other electrons present. This leads to large differences in \(Z_{eff}\) for different elements, as shown in Figure \(\PageIndex{2}\) for the elements of the first three rows of the periodic table.
Penetration describes the proximity to which an electron can approach to the nucleus. In a multi-electron system, electron penetration is defined by an electron's relative electron density (probability density) near the nucleus of an atom (Figure \(\PageIndex{3}\)). Electrons in different orbitals have different electron densities around the nucleus. In other words, penetration depends on the shell (\(n\)) and subshell (\(l\)).
For example, a 1s electron (Figure \(\PageIndex{3}\); purple curve) has greater electron density near the nucleus than a 2p electron (Figure \(\PageIndex{3}\); red curve) and has a greater penetration. This related to the amount of shielding since the 1s electrons are closer to the nucleus than a 2p electron, hence the 1s screens a 2p electron almost perfectly. However, the 2s electron has a lesser amount of shielding because it can penetrate close to the nucleus in the small area of electron density within the first spherical node (Figure \(\PageIndex{3}\); green curve). In this way the 2s electron can "avoid" some of the shielding effect of the inner 1s electron.
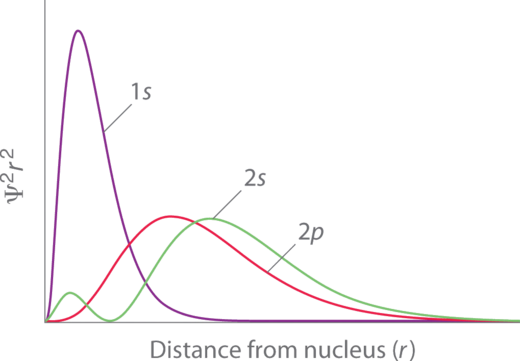
Figure \(\PageIndex{3}\): Orbital Penetration. A comparison of the radial probability distribution of the 2s and 2p orbitals for various states of the hydrogen atom shows that the 2s orbital penetrates inside the 1s orbital more than the 2p orbital does. Consequently, when an electron is in the small inner lobe of the 2s orbital, it experiences a relatively large value of \(Z_{eff}\), which causes the energy of the 2s orbital to be lower than the energy of the 2p orbital.
For the same shell value (\(n\)) the penetrating power of an electron follows this trend in subshells (Figure \(\PageIndex{3}\)):
\[s > p > d \approx f. \label{better1}\]
for different values of shell (n) and subshell (l), penetrating power of an electron follows this trend:
\[\ce{1s > 2s > 2p > 3s > 3p > 4s > 3d > 4p > 5s > 4d > 5p > 6s > 4f ...} \label{better2}\]
Penetration
Penetration describes the proximity of electrons in an orbital to the nucleus. Electrons that have greater penetration can get closer to the nucleus and effectively block out the charge from electrons that have less proximity.
| Atom | Sublevel | Z | Zeff |
|---|---|---|---|
| H | 1s | 1 | 1 |
| He | 1s | 2 | 1.69 |
| Li | 1s, 2s | 3 | 2.69, 1.28 |
| Be | 1s, 2s | 4 | 3.68, 1.91 |
| B | 1s, 2s, 2p | 5 | 4.68, 2.58, 2.42 |
| F | 1s, 2s, 2p | 9 | 8.65, 5.13, 5.10 |
| Na | 1s, 2s, 2p, 3s | 11 | 10.63, 6.57, 6.80, 2.51 |
Data from E. Clementi and D. L. Raimondi; The Journal of Chemical Physics 38, 2686 (1963).
Because of the effects of shielding and the different radial distributions of orbitals with the same value of n but different values of l, the different subshells are not degenerate in a multielectron atom. For a given value of n, the ns orbital is always lower in energy than the np orbitals, which are lower in energy than the nd orbitals, and so forth. As a result, some subshells with higher principal quantum numbers are actually lower in energy than subshells with a lower value of n; for example, the 4s orbital is lower in energy than the 3d orbitals for most atoms.
A Better Estimation of Shielding: Slater's Rules
The concepts of electron shielding, orbital penetration and effective nuclear charge were introduced above, but in a qualitative manner. A more accurate model for estimating electron shielding and corresponding effective nuclear charge quantitatively is Slater's Rules. However, the application of these rules is outside the scope of this text.
Summary
The calculation of orbital energies in atoms or ions with more than one electron (multielectron atoms or ions) is complicated by repulsive interactions between the electrons. The concept of electron shielding, in which intervening electrons act to reduce the positive nuclear charge experienced by an electron, allows the use of hydrogen-like orbitals and an effective nuclear charge (\(Z_{eff}\)) to describe electron distributions in more complex atoms or ions. The degree to which orbitals with different values of l and the same value of n overlap or penetrate filled inner shells results in slightly different energies for different subshells in the same principal shell in most atoms.

