7.6: Hess’s Law

Learning Objective

• Learn how to combine chemical equations and their enthalpy changes.

Now that we understand that chemical reactions occur with a simultaneous change in energy, we can apply the concept more broadly. To start, remember that some chemical reactions are rather difficult to perform. For example, consider the combustion of carbon to make carbon monoxide:

2C(s) + O₂(g) → 2CO(g) ΔH = ?

In reality, this is extremely difficult to do; given the opportunity, carbon will react to make another compound, carbon dioxide:

2C(s) + O₂(g) → 2CO₂(g) ΔH = −393.5 kJ

Is there a way around this? Yes. It comes from the understanding that chemical equations can be treated like algebraic equations, with the arrow acting like the equals sign. Like algebraic equations, chemical equations can be combined, and if the same substance appears on both sides of the arrow, it can be canceled out (much like a spectator ion in ionic equations). For example, consider these two reactions:

2C(s) + 2O₂(g) → 2CO₂(g)2CO₂(g) → 2CO(g) + O₂(g)

If we added these two equations by combining all the reactants together and all the products together, we would get

2C(s) + 2O₂(g) + 2CO₂(g) → 2CO₂(g) + 2CO(g) + O₂(g)

We note that 2CO₂(g) appears on both sides of the arrow, so they cancel:

\[2C(s)+2O_{2}(g)+\not{2CO_{2}(g)}\rightarrow \not{2CO_{2}(g)}+2CO(g)+O_{2}(g)\]

We also note that there are 2 mol of O₂ on the reactant side, and 1 mol of O₂ on the product side. We can cancel 1 mol of O₂ from both sides:

\[2C(s)+2O_{2}(g)\rightarrow 2CO(g)+O_{2}(g)\]

What do we have left?

2C(s) + O₂(g) → 2CO(g)

This is the reaction we are looking for! So by algebraically combining chemical equations, we can generate new chemical equations that may not be feasible to perform.

What about the enthalpy changes? Hess's law states that when chemical equations are combined algebraically, their enthalpies can be combined in exactly the same way. Two corollaries immediately present themselves:

1. If a chemical reaction is reversed, the sign on ΔH is changed.
2. If a multiple of a chemical reaction is taken, the same multiple of the ΔH is taken as well.

What are the equations being combined? The first chemical equation is the combustion of C, which produces CO₂:

2C(s) + 2O₂(g) → 2CO₂(g)

This reaction is two times the reaction to make CO₂ from C(s) and O₂(g), whose enthalpy change is known:

C(s) + O₂(g) → CO₂(g) ΔH = −393.5 kJ

According to the first corollary, the first reaction has an energy change of two times −393.5 kJ, or −787.0 kJ:

2C(s) + 2O₂(g) → 2CO₂(g) ΔH = −787.0 kJ

The second reaction in the combination is related to the combustion of CO(g):

2CO(g) + O₂(g) → 2CO₂(g) ΔH = −566.0 kJ

The second reaction in our combination is the reverse of the combustion of CO. When we reverse the reaction, we change the sign on the ΔH:

2CO₂(g) → 2CO(g) + O₂(g) ΔH = +566.0 kJ

Now that we have identified the enthalpy changes of the two component chemical equations, we can combine the ΔH values and add them:

\[\begin{cases} 2C(s)+2O_{2}(g)\rightarrow 2CO_{2}(g)\; \; \; \; \; \; \Delta H=-787.0kJ\\ \not{2CO_{2}(g)}\rightarrow 2CO(g))+\not{O_{2}(g)}\; \; \, \, \Delta H=+566.0kJ\\ -------------------------\\ 2C(s)+O_{2}(g)\rightarrow 2CO(g)\; \; \; \; \; \; \; \; \; \; \, \Delta H=-787.0+566.0=-221.0kJ\\ \end{cases}\]

Hess’s law is very powerful. It allows us to combine equations to generate new chemical reactions whose enthalpy changes can be calculated, rather than directly measured.

Example \(\PageIndex{1}\):

Determine the enthalpy change of

C₂H₄ + 3O₂ → 2CO₂ + 2H₂O ΔH = ?

from these reactions:

C₂H₂ + H₂ → C₂H₄ ΔH = −174.5 kJ2C₂H₂ + 5O₂ → 4CO₂ + 2H₂O ΔH = −1,692.2 kJ2CO₂ + H₂ → 2O₂ + C₂H₂ ΔH = −167.5 kJ

Solution

We will start by writing chemical reactions that put the correct number of moles of the correct substance on the proper side. For example, our desired reaction has C₂H₄ as a reactant, and only one reaction from our data has C₂H₄. However, it has C₂H₄ as a product. To make it a reactant, we need to reverse the reaction, changing the sign on the ΔH:

C₂H₄ → C₂H₂ + H₂ ΔH = +174.5 kJ

We need CO₂ and H₂O as products. The second reaction has them on the proper side, so let us include one of these reactions (with the hope that the coefficients will work out when all our reactions are added):

2C₂H₂ + 5O₂ → 4CO₂ + 2H₂O ΔH = −1,692.2 kJ

We note that we now have 4 mol of CO₂ as products; we need to get rid of 2 mol of CO₂. The last reaction has 2CO₂ as a reactant. Let us use it as written:

2CO₂ + H₂ → 2O₂ + C₂H₂ ΔH = −167.5 kJ

We combine these three reactions, modified as stated:

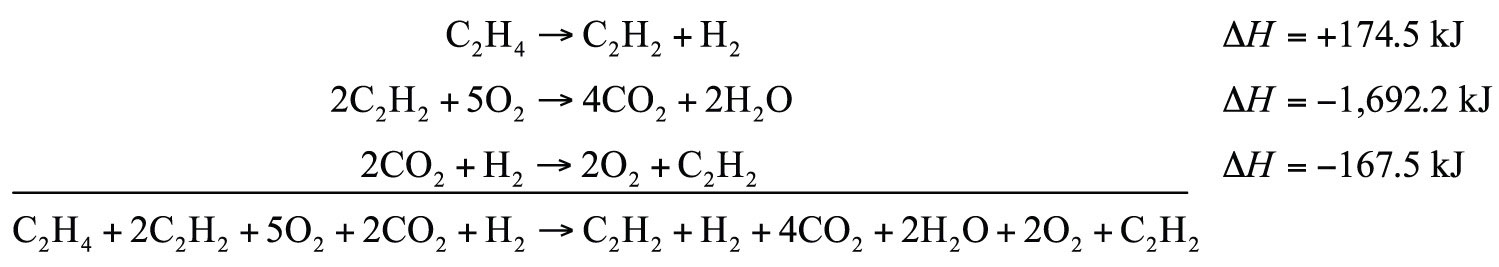
What cancels? 2C₂H₂, H₂, 2O₂, and 2CO₂. What is left is

C₂H₄ + 3O₂ → 2CO₂ + 2H₂O

which is the reaction we are looking for. The ΔH of this reaction is the sum of the three ΔH values:

ΔH = +174.5 − 1,692.2 − 167.5 = −1,685.2 kJ

Exercise \(\PageIndex{1}\)

Test Yourself

Given the thermochemical equations

Pb + Cl₂ → PbCl₂ ΔH = −223 kJPbCl₂ + Cl₂ → PbCl₄ ΔH = −87 kJ

determine ΔH for

2PbCl₂ → Pb + PbCl₄

Answer

+136 kJ

Key Takeaway

• Hess’s law allows us to combine reactions algebraically and then combine their enthalpy changes the same way.

Exercise \(\PageIndex{1}\)

1. Define Hess’s law.

2. What does Hess’s law require us to do to the ΔH of a thermochemical equation if we reverse the equation?

3. If the ΔH for

   C₂H₄ + H₂ → C₂H₆

   is −65.6 kJ, what is the ΔH for this reaction?

   C₂H₆ → C₂H₄ + H₂

4. If the ΔH for

   2Na + Cl₂ → 2NaCl

   is −772 kJ, what is the ΔH for this reaction:

   2NaCl → 2Na + Cl₂

5. If the ΔH for

   C₂H₄ + H₂ → C₂H₆

   is −65.6 kJ, what is the ΔH for this reaction?

   2C₂H₄ + 2H₂ → 2C₂H₆

6. If the ΔH for

   2C₂H₆ + 7O₂ → 4CO₂ + 6H₂O

   is −2,650 kJ, what is the ΔH for this reaction?

   6C₂H₆ + 21O₂ → 12CO₂ + 18H₂O

7. The ΔH for

   C₂H₄ + H₂O → C₂H₅OH

   is −44 kJ. What is the ΔH for this reaction?

   2C₂H₅OH → 2C₂H₄ + 2H₂O

8. The ΔH for

   N₂ + O₂ → 2NO

   is 181 kJ. What is the ΔH for this reaction?

   NO → 1/2N₂ + 1/2O₂

9. Determine the ΔH for the reaction

   Cu + Cl₂ → CuCl₂

   given these data:

   2Cu + Cl₂ → 2CuCl ΔH = −274 kJ2CuCl + Cl₂ → 2CuCl₂ ΔH = −166 kJ

10. Determine ΔH for the reaction

    2CH₄ → 2H₂ + C₂H₄

    given these data:

    CH₄ + 2O₂ → CO₂ + 2H₂O ΔH = −891 kJC₂H₄ + 3O₂ → 2CO₂ + 2H₂O ΔH = −1,411 kJ2H₂ + O₂ → 2H₂O ΔH = −571 kJ

11. Determine ΔH for the reaction

    Fe₂(SO₄)₃ → Fe₂O₃ + 3SO₃

    given these data:

    4Fe + 3O₂ → 2Fe₂O₃ ΔH = −1,650 kJ2S + 3O₂ → 2SO₃ ΔH = −792 kJ2Fe + 3S + 6O₂ → Fe₂(SO₄)₃ ΔH = −2,583 kJ

12. Determine ΔH for the reaction

CaCO₃ → CaO + CO₂

given these data:

2Ca + 2C + 3O₂ → 2CaCO₃ ΔH = −2,414 kJC + O₂ → CO₂ ΔH = −393.5 kJ2Ca + O₂ → 2CaO ΔH = −1,270 kJ

Answers

1. If chemical equations are combined, their energy changes are also combined.

3. ΔH = 65.6 kJ

5. ΔH = −131.2 kJ

7. ΔH = 88 kJ

9. ΔH = −220 kJ

11. ΔH = 570 kJ