6.4: Ionization Energy

Skills to Develop

• To correlate ionization energies with the chemistry of the elements

We have seen that when elements react, they often gain or lose enough electrons to achieve the valence electron configuration of the nearest noble gas. In this section, we develop a more quantitative approach to predicting such reactions by examining periodic trends in the energy changes that accompany ion formation.

Ionization Energies

Because atoms do not spontaneously lose electrons, energy is required to remove an electron from an atom to form a cation. Chemists define the ionization energy (\(I\)) of an element as the amount of energy needed to remove an electron from the gaseous atom \(E\) in its ground state. \(I\) is therefore the energy required for the reaction

\[ E_{(g)} \rightarrow E^+_{(g)} +e^- \;\;\ \text{energy required=I } \tag{7.4.1}\]

Because an input of energy is required, the ionization energy is always positive (\(I > 0\)) for the reaction as written in Equation 7.4.1. Larger values of I mean that the electron is more tightly bound to the atom and harder to remove. Typical units for ionization energies are kilojoules/mole (kJ/mol) or electron volts (eV):

\[1\; eV/atom = 96.49\; kJ/mol\]

If an atom possesses more than one electron, the amount of energy needed to remove successive electrons increases steadily. We can define a first ionization energy (I₁), a second ionization energy (I₂), and in general an nth ionization energy (I_n) according to the following reactions:

\[ E_{(g)} \rightarrow E^+_{(g)} +e^- \;\;\ I_1=\text{1st ionization energy} \tag{7.4.2}\]

\[ E_{(g)} \rightarrow E^+_{(g)} +e^- \;\;\ I_2=\text{2nd ionization energy} \tag{7.4.3}\]

\[ E^+_{(g)} \rightarrow E^{2+}_{(g)} +e^- \;\;\ I_3=\text{3rd ionization energy} \tag{7.4.4}\]

Values for the ionization energies of \(Li\) and \(Be\) listed in Table 7.4.1 show that successive ionization energies for an element increase steadily; that is, it takes more energy to remove the second electron from an atom than the first, and so forth. There are two reasons for this trend. First, the second electron is being removed from a positively charged species rather than a neutral one, so in accordance with Coulomb’s law, more energy is required. Second, removing the first electron reduces the repulsive forces among the remaining electrons, so the attraction of the remaining electrons to the nucleus is stronger.

Note

Successive ionization energies for an element increase steadily.

Table 7.4.1: Ionization Energies (in kJ/mol) for Removing Successive Electrons from Li and Be. Source: Data from CRC Handbook of Chemistry and Physics (2004).

Reaction	Electronic Transition	\[I\]	Reaction	Electronic Transition	\[I\]
\(Li_{(g)}\rightarrow Li^+_{(g)} + e^-\)	\(1s^22s^1 \rightarrow 1s^2\)	I1 = 520.2	\(Be_{(g)} \rightarrow Be^+_{(g)}+e^-\)	\(1s^22s^2 \rightarrow 1s^22s^1\)	I1 = 899.5
\(Li^+_{(g)} \rightarrow Li^{2+}_{(g)} +e^-\)	\(1s^2 \rightarrow 1s^1\)	I2 = 7298.2	\(Be^+_{(g)} \rightarrow Be^{2+}_{(g)} +e^-\)	\(1s^22s^1 \rightarrow 1s^2\)	I2 = 1757.1
\(Li^{2+}_{(g)} \rightarrow Li^{3+}_{(g)} + e^-\)	\(1s^1 \rightarrow 1s^0\)	I3 = 11,815.0	\(Be^{2+}_{(g)} \rightarrow Be^{3+}_{(g)}+e^-\)	\(1s^2 \rightarrow 1s^1\)	I3 = 14,848.8
			\(Be^{3+}_{(g)} \rightarrow Be^{4+}_{(g)}+e^-\)	\(1s^1 \rightarrow 1s^0\)	I4 = 21,006.6

The most important consequence of the values listed in Table 7.4.1 is that the chemistry of \(Li\) is dominated by the \(Li^+\) ion, while the chemistry of \(Be\) is dominated by the +2 oxidation state. The energy required to remove the second electron from \(Li\)

\[Li^+_{(g)} \rightarrow Li^{2+}_{(g)} + e^− \tag{7.4.5}\]

is more than 10 times greater than the energy needed to remove the first electron. Similarly, the energy required to remove the third electron from \(Be\)

\[Be^{2+}_{(g)} \rightarrow Be^{3+}_{(g)} + e^− \tag{7.4.6}\]

is about 15 times greater than the energy needed to remove the first electron and around 8 times greater than the energy required to remove the second electron. Both \(Li^+\) and \(Be^{2+}\) have 1s² closed-shell configurations, and much more energy is required to remove an electron from the 1s² core than from the 2s valence orbital of the same element. The chemical consequences are enormous: lithium (and all the alkali metals) forms compounds with the 1+ ion but not the 2+ or 3+ ions. Similarly, beryllium (and all the alkaline earth metals) forms compounds with the 2+ ion but not the 3+ or 4+ ions. The energy required to remove electrons from a filled core is prohibitively large and simply cannot be achieved in normal chemical reactions.

Note

The energy required to remove electrons from a filled core is prohibitively large under normal reaction conditions.

Ionization Energies of s- and p-Block Elements

Ionization energies of the elements in the third row of the periodic table exhibit the same pattern as those of \(Li\) and \(Be\) (Table 7.4.2): successive ionization energies increase steadily as electrons are removed from the valence orbitals (3s or 3p, in this case), followed by an especially large increase in ionization energy when electrons are removed from filled core levels as indicated by the bold diagonal line in Table 7.4.2. Thus in the third row of the periodic table, the largest increase in ionization energy corresponds to removing the fourth electron from \(Al\), the fifth electron from Si, and so forth—that is, removing an electron from an ion that has the valence electron configuration of the preceding noble gas. This pattern explains why the chemistry of the elements normally involves only valence electrons. Too much energy is required to either remove or share the inner electrons.

Table 7.4.2: Successive Ionization Energies (in kJ/mol) for the Elements in the Third Row of the Periodic Table.Source: Data from CRC Handbook of Chemistry and Physics (2004).

Element	I 1	I 2	I 3	I 4	I 5	I 6	I 7
*Inner-shell electron
Na	495.8	4562.4*	—	—	—	—	—
Mg	737.7	1450.7	7732.7	—	—	—	—
Al	577.4.4	1816.7	2744.8	11,577.4.4	—	—	—
Si	786.5	1577.1	3231.6	4355.5	16,090.6	—	—
P	1011.8	1907.4.4	2914.1	4963.6	6274.0	21,267.4.3	—
S	999.6	2251.8	3357	4556.2	7004.3	8495.8	27,107.4.3
Cl	1251.2	2297.7	3822	5158.6	6540	9362	11,018.2
Ar	1520.6	2665.9	3931	5771	7238	8781.0	11,995.3

Example 7.4.1: Highest Fourth Ionization Energy

From their locations in the periodic table, predict which of these elements has the highest fourth ionization energy: B, C, or N.

Given: three elements

Asked for: element with highest fourth ionization energy

Strategy:

1. List the electron configuration of each element.
2. Determine whether electrons are being removed from a filled or partially filled valence shell. Predict which element has the highest fourth ionization energy, recognizing that the highest energy corresponds to the removal of electrons from a filled electron core.

Solution:

A These elements all lie in the second row of the periodic table and have the following electron configurations:

• B: [He]2s²2p¹
• C: [He]2s²2p²
• N: [He]2s²2p³

B The fourth ionization energy of an element (\(I_4\)) is defined as the energy required to remove the fourth electron:

\[E^{3+}_{(g)} \rightarrow E^{4+}_{(g)} + e^-\]

Because carbon and nitrogen have four and five valence electrons, respectively, their fourth ionization energies correspond to removing an electron from a partially filled valence shell. The fourth ionization energy for boron, however, corresponds to removing an electron from the filled 1s² subshell. This should require much more energy. The actual values are as follows: B, 25,026 kJ/mol; C, 6223 kJ/mol; and N, 7475 kJ/mol.

Exercise 7.4.1: Lowest Second Ionization Energy

From their locations in the periodic table, predict which of these elements has the lowest second ionization energy: Sr, Rb, or Ar.

Answer: Sr

The first column of data in Table 7.4.2 shows that first ionization energies tend to increase across the third row of the periodic table. This is because the valence electrons do not screen each other very well, allowing the effective nuclear charge to increase steadily across the row. The valence electrons are therefore attracted more strongly to the nucleus, so atomic sizes decrease and ionization energies increase. These effects represent two sides of the same coin: stronger electrostatic interactions between the electrons and the nucleus further increase the energy required to remove the electrons.

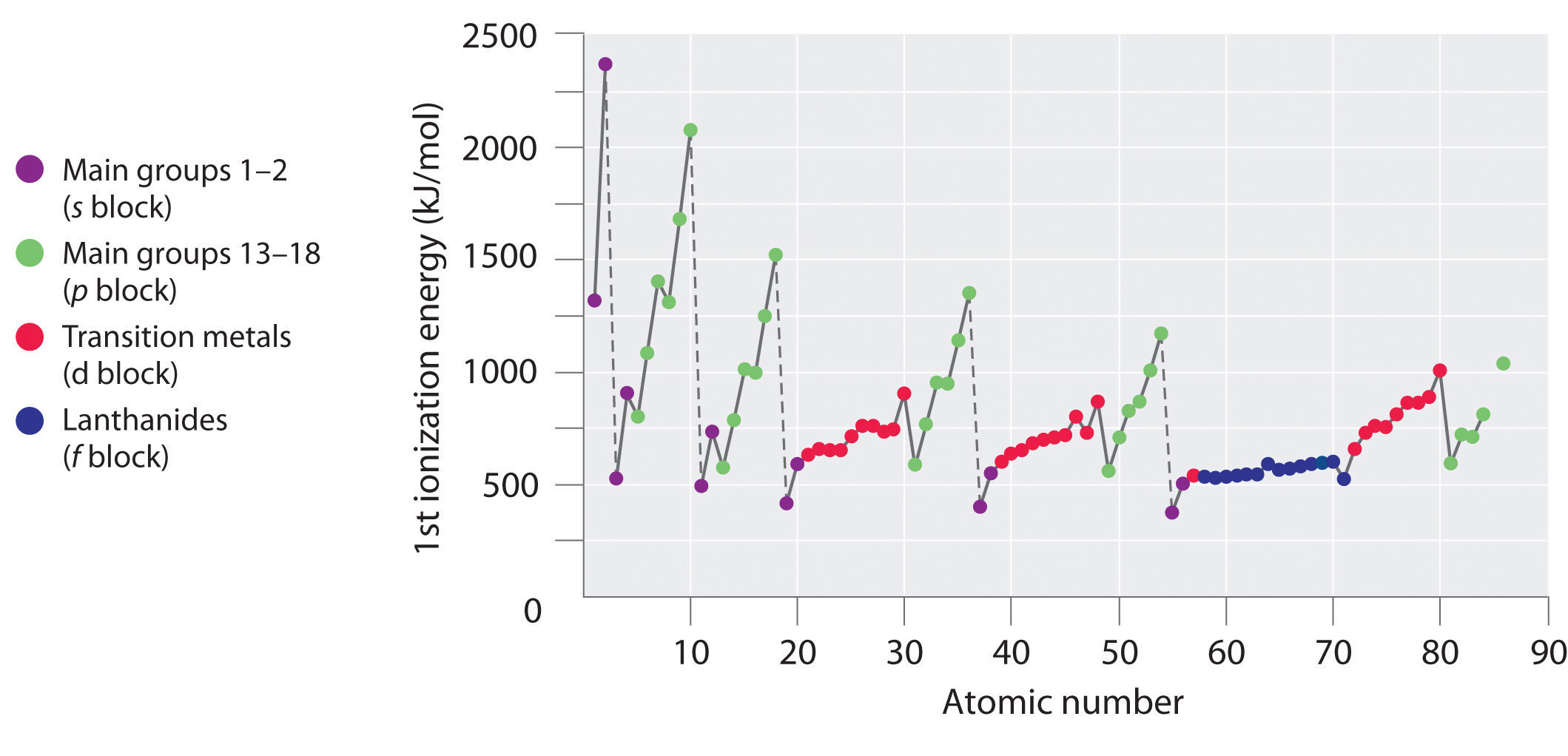
Figure 7.4.1: A Plot of Periodic Variation of First Ionization Energy with Atomic Number for the First Six Rows of the Periodic Table. There is a decrease in ionization energy within a group (most easily seen here for groups 1 and 18).

However, the first ionization energy decreases at Al ([Ne]3s²3p¹) and at S ([Ne]3s²3p⁴). The electrons in aluminum’s filled 3s² subshell are better at screening the 3p¹ electron than they are at screening each other from the nuclear charge, so the s electrons penetrate closer to the nucleus than the p electron does. The decrease at S occurs because the two electrons in the same p orbital repel each other. This makes the S atom slightly less stable than would otherwise be expected, as is true of all the group 16 elements.

Figure 7.4.2: First Ionization Energies of the s-, p-, d-, and f-Block Elements

The first ionization energies of the elements in the first six rows of the periodic table are plotted in Figure 7.4.1 and are presented numerically and graphically in Figure 7.4.2. These figures illustrate three important trends:

1. The changes seen in the second (Li to Ne), fourth (K to Kr), fifth (Rb to Xe), and sixth (Cs to Rn) rows of the s and p blocks follow a pattern similar to the pattern described for the third row of the periodic table. The transition metals are included in the fourth, fifth, and sixth rows, however, and the lanthanides are included in the sixth row. The first ionization energies of the transition metals are somewhat similar to one another, as are those of the lanthanides. Ionization energies increase from left to right across each row, with discrepancies occurring at ns²np¹ (group 13), ns²np⁴ (group 16), and ns²(n − 1)d¹⁰ (group 12) electron configurations.
2. First ionization energies generally decrease down a column. Although the principal quantum number n increases down a column, filled inner shells are effective at screening the valence electrons, so there is a relatively small increase in the effective nuclear charge. Consequently, the atoms become larger as they acquire electrons. Valence electrons that are farther from the nucleus are less tightly bound, making them easier to remove, which causes ionization energies to decrease. A larger radius corresponds to a lower ionization energy.
3. Because of the first two trends, the elements that form positive ions most easily (have the lowest ionization energies) lie in the lower left corner of the periodic table, whereas those that are hardest to ionize lie in the upper right corner of the periodic table. Consequently, ionization energies generally increase diagonally from lower left (Cs) to upper right (He).

Note

Generally, \(I_1\) increases diagonally from the lower left of the periodic table to the upper right.

The darkness of the shading inside the cells of the table indicates the relative magnitudes of the ionization energies. Elements in gray have undetermined first ionization energies. Source: Data from CRC Handbook of Chemistry and Physics (2004).

Gallium (Ga), which is the first element following the first row of transition metals, has the following electron configuration: [Ar]4s²3d¹⁰4p¹. Its first ionization energy is significantly lower than that of the immediately preceding element, zinc, because the filled 3d¹⁰ subshell of gallium lies inside the 4p subshell, screening the single 4p electron from the nucleus. Experiments have revealed something of even greater interest: the second and third electrons that are removed when gallium is ionized come from the 4s² orbital, not the 3d¹⁰ subshell. The chemistry of gallium is dominated by the resulting Ga³⁺ ion, with its [Ar]3d¹⁰ electron configuration. This and similar electron configurations are particularly stable and are often encountered in the heavier p-block elements. They are sometimes referred to as pseudo noble gas configurations. In fact, for elements that exhibit these configurations, no chemical compounds are known in which electrons are removed from the (n − 1)d¹⁰ filled subshell.

Ionization Energies of Transition Metals & Lanthanides

As we noted, the first ionization energies of the transition metals and the lanthanides change very little across each row. Differences in their second and third ionization energies are also rather small, in sharp contrast to the pattern seen with the s- and p-block elements. The reason for these similarities is that the transition metals and the lanthanides form cations by losing the ns electrons before the (n − 1)d or (n − 2)f electrons, respectively. This means that transition metal cations have (n − 1)dⁿ valence electron configurations, and lanthanide cations have (n − 2)fⁿ valence electron configurations. Because the (n − 1)d and (n − 2)f shells are closer to the nucleus than the ns shell, the (n − 1)d and (n − 2)f electrons screen the ns electrons quite effectively, reducing the effective nuclear charge felt by the ns electrons. As Z increases, the increasing positive charge is largely canceled by the electrons added to the (n − 1)d or (n − 2)f orbitals.

That the ns electrons are removed before the (n − 1)d or (n − 2)f electrons may surprise you because the orbitals were filled in the reverse order. In fact, the ns, the (n − 1)d, and the (n − 2)f orbitals are so close to one another in energy, and interpenetrate one another so extensively, that very small changes in the effective nuclear charge can change the order of their energy levels. As the d orbitals are filled, the effective nuclear charge causes the 3d orbitals to be slightly lower in energy than the 4s orbitals. The [Ar]3d² electron configuration of Ti²⁺ tells us that the 4s electrons of titanium are lost before the 3d electrons; this is confirmed by experiment. A similar pattern is seen with the lanthanides, producing cations with an (n − 2)fⁿ valence electron configuration.

Because their first, second, and third ionization energies change so little across a row, these elements have important horizontal similarities in chemical properties in addition to the expected vertical similarities. For example, all the first-row transition metals except scandium form stable compounds as M²⁺ ions, whereas the lanthanides primarily form compounds in which they exist as M³⁺ ions.

Example 7.4.2: Lowest First Ionization Energy

Use their locations in the periodic table to predict which element has the lowest first ionization energy: Ca, K, Mg, Na, Rb, or Sr.

Given: six elements

Asked for: element with lowest first ionization energy

Strategy:

Locate the elements in the periodic table. Based on trends in ionization energies across a row and down a column, identify the element with the lowest first ionization energy.

Solution:

These six elements form a rectangle in the two far-left columns of the periodic table. Because we know that ionization energies increase from left to right in a row and from bottom to top of a column, we can predict that the element at the bottom left of the rectangle will have the lowest first ionization energy: Rb.

Exercise 7.4.2: Highest First Ionization Energy

Use their locations in the periodic table to predict which element has the highest first ionization energy: As, Bi, Ge, Pb, Sb, or Sn.

Answer: As

Summary

• Generally, the first ionization energy and electronegativity values increase diagonally from the lower left of the periodic table to the upper right, and electron affinities become more negative across a row.

The tendency of an element to lose is one of the most important factors in determining the kind of compounds it forms. Periodic behavior is most evident for ionization energy (I), the energy required to remove an electron from a gaseous atom. The energy required to remove successive electrons from an atom increases steadily, with a substantial increase occurring with the removal of an electron from a filled inner shell. Consequently, only valence electrons can be removed in chemical reactions, leaving the filled inner shell intact. Ionization energies explain the common oxidation states observed for the elements. Ionization energies increase diagonally from the lower left of the periodic table to the upper right. Minor deviations from this trend can be explained in terms of particularly stable electronic configurations, called pseudo noble gas configurations, in either the parent atom or the resulting ion.