6.1: Heat Flow
- Page ID
- 58813
Learning Outcomes
- Describe how chemical potential energy relates to heat and work.
- Use the specific heat equation to perform calculations that relate mass, specific heat, change in temperature, and the amount of heat absorbed or released.
- Convert among joule, calorie, and Calorie.
- Define endothermic and exothermic.
- Explain the difference between heat and specific heat capacity.
Chemical reactions are accompanied by transfers of energy. Keeping track of heat flow and energy requirements is important for a full understanding of chemical processes. Energy is the capacity for doing work or supplying heat. When you fill your car with gasoline, you are providing it with potential energy. Chemical potential energy is the energy stored in the chemical bonds of a substance. The various chemicals in gasoline contain a large amount of chemical potential energy that is released when the gasoline is burned in a controlled way in the engine of the car. The release of that energy does two things. Some of the potential energy is transformed into work, which is used to move the car (see figure below). At the same time, some of the potential energy is converted to heat, making the car's engine very hot. The energy changes of a system occur as either heat or work, or some combination of both.

Heat is energy that is transferred from one object or substance to another because of a difference in temperature between them. Heat always flows from an object at a higher temperature to an object at a lower temperature (see figure below). The flow of heat will continue until the two objects are at the same temperature.

Thermochemistry is the study of energy changes that occur during chemical reactions and during changes of state. When chemical reactions occur, some chemical bonds are broken, while new chemical bonds form. As a result of the rearrangement of atoms, the total chemical potential energy of the system either increases or decreases.
Exothermic and Endothermic Processes
When physical or chemical changes occur, they are generally accompanied by a transfer of energy. The law of conservation of energy states that in any physical or chemical process, energy is neither created nor destroyed. In other words, the entire energy in the universe is conserved. In order to better understand the energy changes taking place during a reaction, we need to define two parts of the universe, called the system and the surroundings. The system is the specific portion of matter in a given space that is being studied during an experiment or an observation. The surroundings is everything in the universe that is not part of the system. In practical terms for a laboratory chemist, the system is generally the reaction being investigated, while the surroundings include the immediate vicinity within the room. During most processes, energy is exchanged between the system and the surroundings. If the system loses a certain amount of energy, that same amount of energy is gained by the surroundings. If the system gains a certain amount of energy, that energy is supplied by the surroundings.
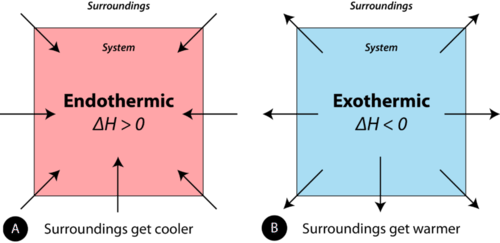
In the study of thermochemical processes, things are viewed from the point of view of the system. A chemical reaction or physical change is endothermic if heat is absorbed by the system from the surroundings. In the course of an endothermic process, the system gains heat from the surroundings, so the temperature of the surroundings decreases. The quantity of heat for a process is represented by the letter \(q\). The sign of \(q\) for an endothermic process is positive because the system is gaining heat. A chemical reaction or physical change is exothermic if heat is released by the system into the surroundings. Because the surroundings are gaining heat from the system, the temperature of the surroundings increases. The sign of \(q\) for an exothermic process is negative because the system is losing heat. The difference between an endothermic reaction and an exothermic reaction is illustrated below (see figure below).
Units of Heat
Heat flow is measured in one of two common units: the calorie and the joule. The joule \(\left( \text{J} \right)\) is the SI unit of energy. The calorie is familiar because it is commonly used when referring to the amount of energy contained within food. A calorie \(\left( \text{cal} \right)\) is the quantity of heat required to raise the temperature of 1 gram of water by \(1^\text{o} \text{C}\). For example, raising the temperature of \(100 \: \text{g}\) of water from \(20^\text{o} \text{C}\) to \(22^\text{o} \text{C}\) would require \(100 \times 2 = 200 \: \text{cal}\).
Calories contained within food are actually kilocalories \(\left( \text{kcal} \right)\). In other words, if a certain snack contains 85 food Calories, it actually contains \(85 \: \text{kcal}\) or \(85,000 \: \text{cal}\). In order to make the distinction, the dietary calorie is written with a capital C.
\[1 \: \text{kilocalorie} = 1 \: \text{Calorie} = 1000 \: \text{calories}\]
To say that the snack "contains" 85 Calories means that \(85 \: \text{kcal}\) of energy are released when that snack is processed by your body.
Heat changes in chemical reactions are typically measured in joules rather than calories. The conversion between a joule and a calorie is shown below.
\[1 \: \text{J} = 0.2390 \: \text{cal} \: \text{or} \: 1 \: \text{cal} = 4.184 \: \text{J}\]
Example \(\PageIndex{1}\)
How many joules of energy are released when a 400. Calorie hamburger is digested?
Solution
Use the relationship between Calories and calories which is 1000 calories \(=\) 1 Calorie and the conversion factor for joules to calories to find the value in joules. Note that all of the units cancel except joules which is what is being asked for in the question.
\[400 \: \text{Cal} \left( \frac{1000 \: \text{cal}}{1 \: \text{Cal}} \right) \left( \frac{4.184 \: \text{J}}{1 \: \text{cal}} \right) = 1.67 \times 10^6 \: \text{J}\]
Heat Capacity and Specific Heat
If a swimming pool and a bucket, both full of water at the same temperature, were subjected to the same input of heat energy, the bucket of water would certainly rise in temperature more quickly than the swimming pool. Heat capacity is the amount of heat required to raise the temperature of an object by \(1^\text{o} \text{C}\). The heat capacity of an object depends both on its mass and its chemical composition. Because of its much larger mass, the swimming pool of water has a larger heat capacity than the bucket of water.
Different substances respond to heat in different ways. If a metal chair sits in the bright sun on a hot day, it may become quite hot to the touch. An equal mass of water in the same sun will not become nearly as hot. Water is very resistant to changes in temperature, while metals in general are not. The specific heat of a substance is the amount of energy required to raise the temperature of 1 gram of the substance by \(1^\text{o} \text{C}\). The table below lists the specific heat of some common substances. The symbol for specific heat is \(C_p\), with the \(p\) subscript referring to the fact that specific heats are measured at constant pressure. The units for specific heat can either be joules per gram per degree \(\left( \text{J/g} \cdot ^\text{o} \text{C} \right)\), or calories per gram per degree \(\left( \text{cal/g} \cdot ^\text{o} \text{C} \right)\). This text will use \(\text{J/g} \cdot ^\text{o} \text{C}\) for specific heat. Note that the specific heat of a substance depends not only on its identity but also its state. For example, ice, liquid water, and steam all have different specific heat values.
Table \(\PageIndex{1}\): Specific Heats of Some Common Substances
| Substance | Specific Heat \(\left( \text{J/g} \cdot ^\text{o} \text{C} \right)\) |
| Water \(\left( l \right)\) | 4.18 |
| Water \(\left( s \right)\) | 2.06 |
| Water \(\left( g \right)\) | 1.87 |
| Ammonia \(\left( g \right)\) | 2.09 |
| Ethanol \(\left( l \right)\) | 2.44 |
| Aluminum \(\left( s \right)\) | 0.897 |
| Carbon, graphite \(\left( s \right)\) | 0.709 |
| Copper \(\left( s \right)\) | 0.385 |
| Gold \(\left( s \right)\) | 0.129 |
| Iron \(\left( s \right)\) | 0.449 |
| Lead \(\left( s \right)\) | 0.129 |
| Mercury \(\left( l \right)\) | 0.140 |
| Silver \(\left( s \right)\) | 0.233 |
Notice that water has a very high specific heat compared to most other substance. Water is commonly used as a coolant for machinery because it is able to absorb large quantities of heat (see figure below). Coastal climates are much more moderate than inland climates because of the presence of the ocean. Water in lakes or oceans absorbs heat from the air on hot days and releases it back into the air on cool days.

Specific Heat Calculations
The specific heat of a substance can be used to calculate the temperature change that a given substance will undergo when it is either heated or cooled. The equation that relates heat \(\left( q \right)\) to specific heat \(\left( C_p \right)\), mass \(\left( m \right)\), and temperature change \(\left( \Delta T \right)\) is shown below.
\[q = m \times C_p \times \Delta T\]
The heat that is either absorbed or released is measured in joules. The mass is measured in grams. The change in temperature is given by \(\Delta T = T_f - T_i\), where \(T_f\) is the final temperature and \(T_i\) is the initial temperature.
Example \(\PageIndex{2}\)
A \(15.0 \: \text{g}\) piece of cadmium metal absorbs \(134 \: \text{J}\) of heat as its temperature is increased from \(24.0^\text{o} \text{C}\) to \(62.7^\text{o} \text{C}\). Calculate the specific heat of cadmium.
Solution
Step 1: List the known quantities and plan the problem.
Known
- Heat \(= q = 134 \: \text{J}\)
- Mass \(= m = 15.0 \: \text{g}\)
- \(\Delta T = 62.7^\text{o} \text{C} - 24.0^\text{o} \text{C} = 38.7^\text{o} \text{C}\)
Unknown
- \(C_p\) of cadmium \(= ? \: \text{J/g} \cdot ^\text{o} \text{C}\)
The specific heat equation can be rearranged to solve for the specific heat.
Step 2: Solve.
\[C_p = \frac{q}{m \times \Delta T} = \frac{134 \: \text{J}}{15.0 \: \text{g} \times 38.7^\text{o} \text{C}} = 0.231 \: \text{J/g} \cdot ^\text{o} \text{C}\]
Step 3: Think about your result.
The specific heat of cadmium, a metal, is fairly close to the specific heats of other metals in the table above. The result has three significant figures.
Since most specific heats are known, they can be used to determine the final temperature attained by a substance when it is either heated or cooled. Suppose that a \(60.0 \: \text{g}\) sample of water at \(23.52^\text{o} \text{C}\) was cooled by the removal fo \(813 \: \text{J}\) of heat. The change in temperature can be calculated using the specific heat equation.
\[\Delta T = \frac{q}{C_p \times m} = \frac{-813 \: \text{J}}{4.18 \: \text{J/g} \cdot ^\text{o} \text{C} \times 60.0 \: \text{g}} = -3.24^\text{o} \text{C}\]
Since the water was being cooled, heat is removed from the system. Therefore, \(q\) is negative, and the temperature decreases. The final temperature is:
\[T_f = 23.52^\text{o} \text{C} - 3.24^\text{o} \text{C} = 20.28^\text{o} \text{C}\]
Supplemental Resources
- Energy in Chemical Reactions: http://www.wisc-online.com/Objects/V...spx?ID=GCH8705
Contributors and Attributions
Allison Soult, Ph.D. (Department of Chemistry, University of Kentucky)

