5.1: Brønsted–Lowry Acids and Bases

Last updated
Save as PDF

Page ID: 28108

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

In 1923, chemists Johannes Brønsted and Martin Lowry independently developed definitions of acids and bases based on compounds abilities to either donate or accept protons (H⁺ ions). Here, acids are defined as being able to donate protons in the form of hydrogen ions; whereas bases are defined as being able to accept protons. This took the Arrhenius definition one step further as water is no longer required to be present in the solution for acid and base reactions to occur.

Brønsted-Lowery Definition

J.N. Brønsted and T.M. Lowry independently developed the theory of proton donors and proton acceptors in acid-base reactions, coincidentally in the same region and during the same year. The Arrhenius theory where acids and bases are defined by whether the molecule contains hydrogen and hydroxide ion is too limiting. The main effect of the Brønsted-Lowry definition is to identify the proton (H+) transfer occurring in the acid-base reaction. This is best illustrated in the following equation:

\[HA+Z \rightleftharpoons A^− + HZ^+\]

Acid	Base
Donates hydrogen ions	Accepts hydrogen ions.
HCl⁺	HOH →	H₃O⁺ + Cl^-
HOH⁺	NH₃→	NH₄⁺ + OH^-

The determination of a substance as a Brønsted-Lowery acid or base can only be done by observing the reaction. In the case of the HOH it is a base in the first case and an acid in the second case.

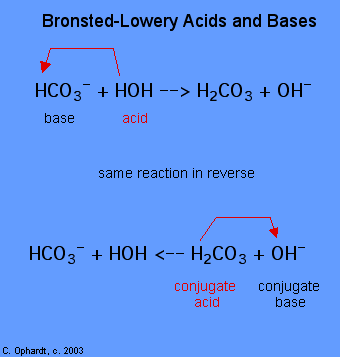
To determine whether a substance is an acid or a base, count the hydrogens on each substance before and after the reaction. If the number of hydrogens has decreased that substance is the acid (donates hydrogen ions). If the number of hydrogens has increased that substance is the base (accepts hydrogen ions). These definitions are normally applied to the reactants on the left. If the reaction is viewed in reverse a new acid and base can be identified. The substances on the right side of the equation are called conjugate acid and conjugate base compared to those on the left. Also note that the original acid turns in the conjugate base after the reaction is over.

Acids are Proton Donors and Bases are Proton Acceptors

For a reaction to be in equilibrium a transfer of electrons needs to occur. The acid will give an electron away and the base will receive the electron. Acids and Bases that work together in this fashion are called a conjugate pair made up of conjugate acids and conjugate bases.

\[ HA + Z \rightleftharpoons A^- + HZ^+ \]

A stands for an Acidic compound and Z stands for a Basic compound

A Donates H to form HZ⁺.
Z Accepts H from A which forms HZ⁺
A^- becomes conjugate base of HA and in the reverse reaction it accepts a H from HZ to recreate HA in order to remain in equilibrium
HZ⁺ becomes a conjugate acid of Z and in the reverse reaction it donates a H to A^- recreating Z in order to remain in equilibrium

Questions

Why is \(HA\) an Acid?
Why is \(Z^-\) a Base?
How can A^- be a base when HA was and Acid?
How can HZ⁺ be an acid when Z used to be a Base?

Now that we understand the concept, let's look at an an example with actual compounds!

\[HCl + H_2O \rightleftharpoons H_3O^+ + Cl^¯\]

HCL is the acid because it is donating a proton to H₂O
H₂O is the base because H₂O is accepting a proton from HCL
H₃O⁺ is the conjugate acid because it is donating an acid to CL turn into it's conjugate acid H₂O
Cl¯ is the conjugate base because it accepts an H from H₃O to return to it's conjugate acid HCl

How can H₂O be a base? I thought it was neutral?

Answers

It has a proton that can be transferred
It receives a proton from HA
A^- is a conjugate base because it is in need of a H in order to remain in equilibrium and return to HA
HZ⁺ is a conjugate acid because it needs to donate or give away its proton in order to return to it's previous state of Z
In the Brønsted-Lowry Theory what makes a compound an element or a base is whether or not it donates or accepts protons. If the H₂O was in a different problem and was instead donating an H rather than accepting an H it would be an acid!

Conjugate Acid–Base Pairs

In aqueous solutions, acids and bases can be defined in terms of the transfer of a proton from an acid to a base. Thus for every acidic species in an aqueous solution, there exists a species derived from the acid by the loss of a proton. These two species that differ by only a proton constitute a conjugate acid–base pair.

All acid–base reactions contain two conjugate acid–base pairs.

For example, in the reaction of HCl with water, HCl, the parent acid, donates a proton to a water molecule, the parent base, thereby forming Cl^-. Thus HCl and Cl^- constitute a conjugate acid–base pair. By convention, we always write a conjugate acid–base pair as the acid followed by its conjugate base. In the reverse reaction, the Cl^- ion in solution acts as a base to accept a proton from H₂O and HCl. Thus H₃O⁺ and H₂O constitute a second conjugate acid–base pair. In general, any acid–base reaction must contain two conjugate acid–base pairs, which in this case are HCl/Cl- and H₃O⁺/H₂O.

File:Wikitexts/UC_Davis/UCD_Chem_2B/UCD_Chem_2B:_Larsen/Unit_III:_Acids_and_Bases/16.2:_A_Qualitative_Description_of_Acid–Base_Equilibria/13307049a0af1fc2a8588ee638396963.jpg

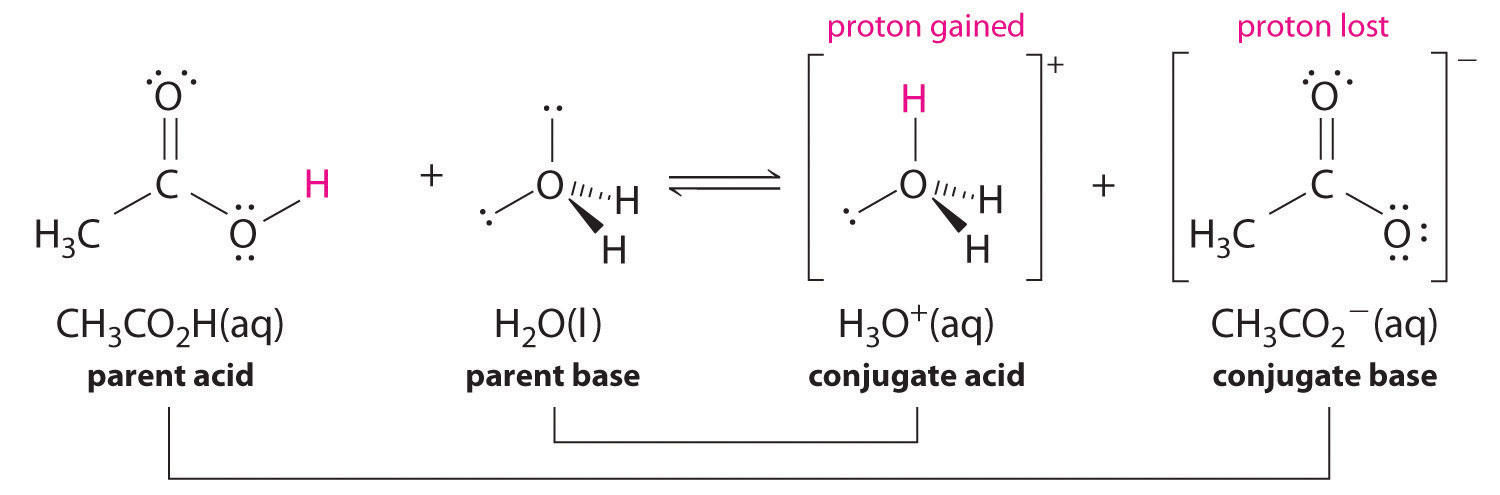
Similarly, in the reaction of acetic acid with water, acetic acid donates a proton to water, which acts as the base. In the reverse reaction, \(H_3O^+\) is the acid that donates a proton to the acetate ion, which acts as the base. Once again, we have two conjugate acid–base pairs: the parent acid and its conjugate base (CH₃CO₂H/CH₃CO₂^-) and the parent base and its conjugate acid (H₃O⁺/H₂O).

File:Wikitexts/UC_Davis/UCD_Chem_2B/UCD_Chem_2B:_Larsen/Unit_III:_Acids_and_Bases/16.2:_A_Qualitative_Description_of_Acid–Base_Equilibria/0976fc4b1971263ab1f1bf651617f1a6.jpg — Figure \(\PageIndex{2}\)

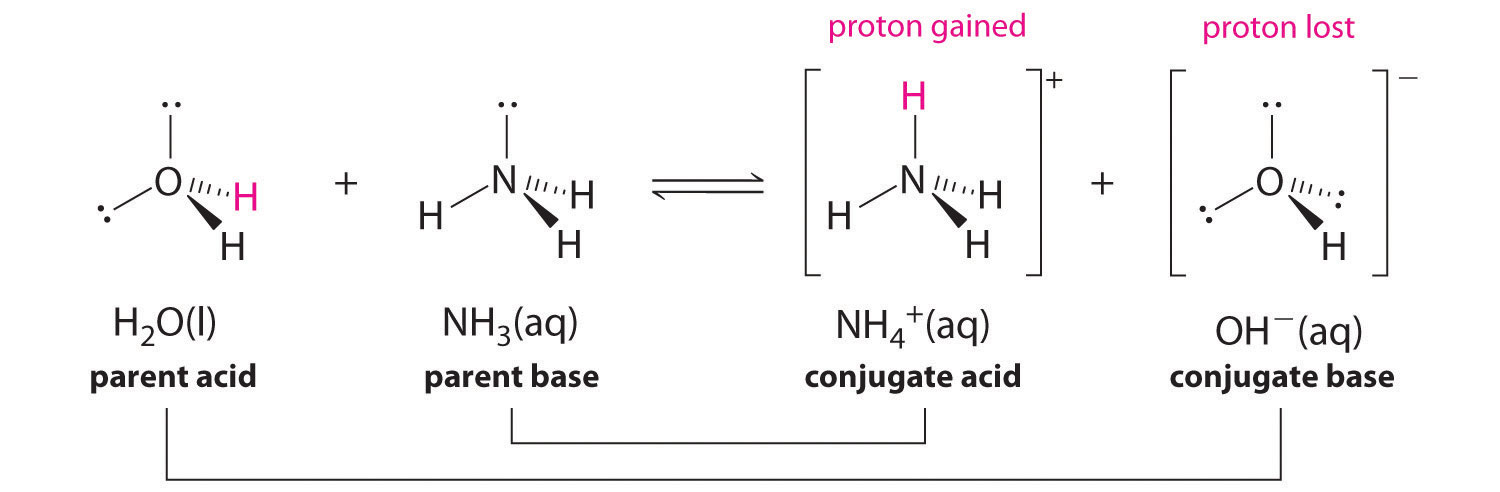
In the reaction of ammonia with water to give ammonium ions and hydroxide ions (Figure 16.3), ammonia acts as a base by accepting a proton from a water molecule, which in this case means that water is acting as an acid. In the reverse reaction, an ammonium ion acts as an acid by donating a proton to a hydroxide ion, and the hydroxide ion acts as a base. The conjugate acid–base pairs for this reaction are NH₄⁺/NH₃ and H₂O/OH^-.