13.10: Irreducible Representation of Point Groups
- Page ID
- 51079
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
There exists an important fact about normal coordinates. Each of these coordinates belongs to an irreducible representation of the point the molecule under investigation. Vibrational wavefunctions associated with vibrational energy levels share this property as well. The normal coordinates and the vibration wavefunction can be categorized further according to the point group they belong to. From the character table predictions can be made for which symmetries can exist. The irreducible representation offers insight into the IR and/or Raman activity of the molecule in question.
Symmetry of normal modes
It is important to realize that every normal mode has a certain type of symmetry associated with it. Identifying the point group of the molecule is therefore an important step. With this in mind it is not surprising that every normal mode forms a basis set for an irreducible representation of the point group the molecule belongs to. For a molecule such as water, having a structure of \(\ce{XY2}\), three normal coordinates can be determined. The two stretching modes are equivalent in symmetry and energy. The figure below shows the three normal modes for the water molecule:
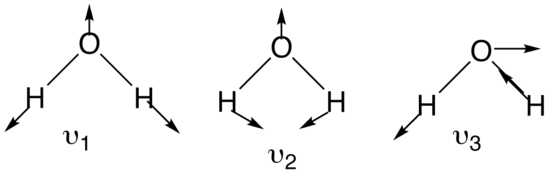
By convention, with nonlinear molecules, the symmetric stretch is denoted v1 whereas the asymmetric stretch is denoted v2. Bending motions are v3. With linear molecules, the bending motion is \(\nu_2\) whereas asymmetric stretch is v3.
The water molecule has C2v symmetry and its symmetry elements are E, C2, σ(xz) and σ(yz). To determine the symmetries of the three vibrations and how they each transform, symmetry operations will be performed. As an example, performing C2 operations using the two normal mode v2 and v3 gives the following transformation:

Once all the symmetry operations have been performed in a systematic manner for each modes the symmetry can be assigned to the normal mode using the character table for C2v:
| C2v | E | C2 | σ (xz) | σ (yz) | |
|---|---|---|---|---|---|
| ν1 | 1 | 1 | 1 | 1 | = a1 |
| ν2 | 1 | 1 | 1 | 1 | = a1 |
| ν3 | 1 | -1 | -1 | 1 | = b2 |
Water has three normal modes that can be grouped together as the reducible representation
\[Γ_{vib}= 2a_1 + b_2. \nonumber \]
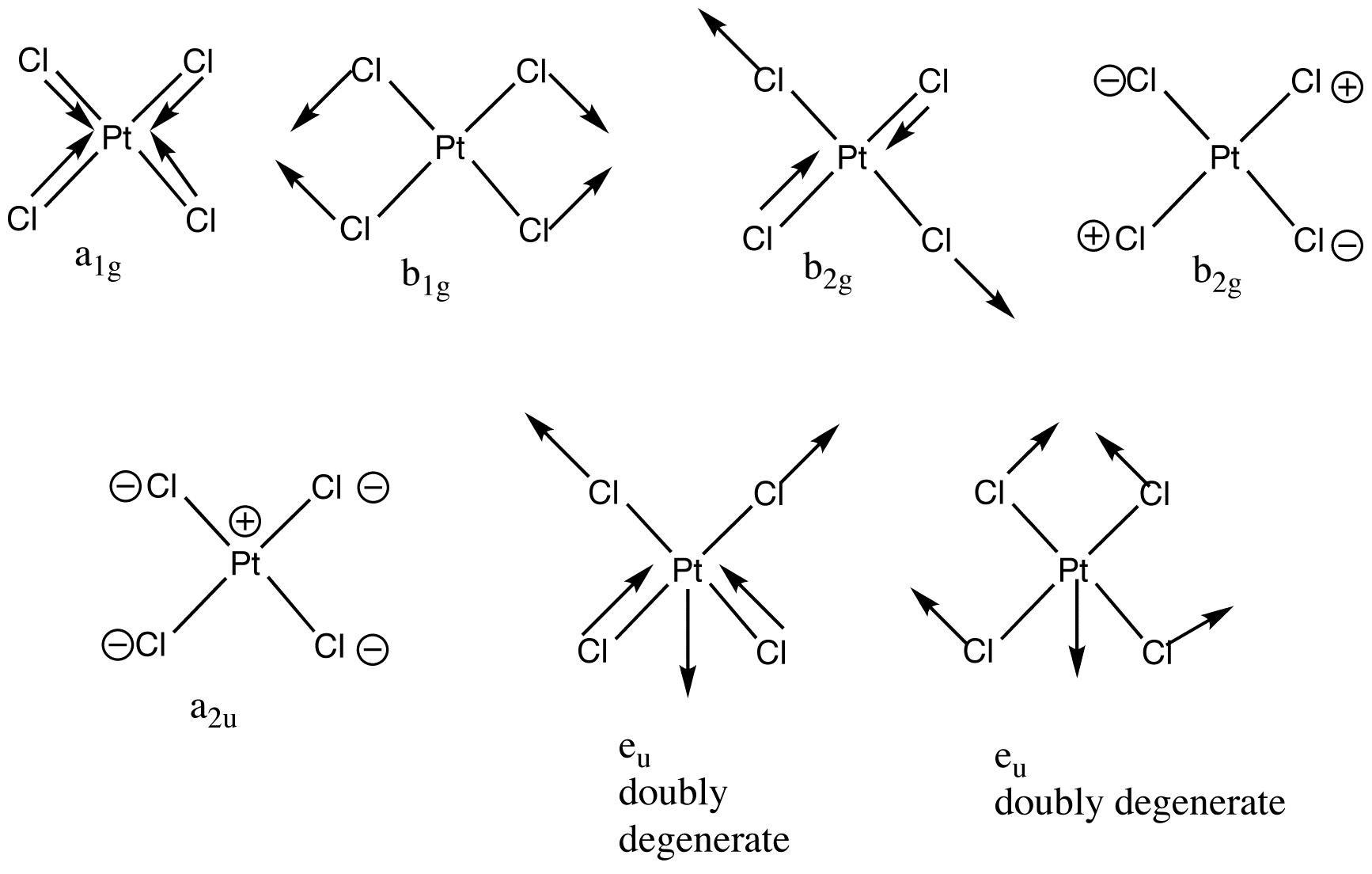
Determination of normal modes becomes quite complex as the number of atoms in the molecule increases. Nowadays, computer programs that simulate molecular vibrations can be used to perform these calculations. The example of [PtCl4]2- shows the increasing complexity (Figure 13.10.2 ). The molecule has five atoms and therefore 15 degrees of freedom, 9 of these are vibrational degrees of freedom. The nine normal modes are exemplified below along with the irreducible representation the normal mode belongs to (D4h point group).