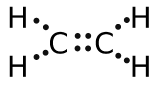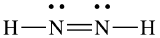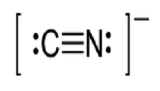Solutions 17
- Page ID
- 47400
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
S17.1
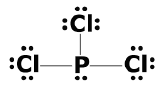
(a) eight electrons:
 ;
;
(b) eight electrons:
 ;
;
(c) no electrons
Be2+;
(d) eight electrons:
 ;
;
(e) no electrons
Ga3+;
(f) no electrons
Li+;
(g) eight electrons:

S17.2
Write Lewis structures for the following:
a. H2

b. HBr
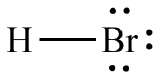
c. PCl3
d. SF2
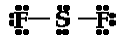
e. H2CCH2
f. HNNH
g. H2CNH

h. NO–
i. N2
j. CO
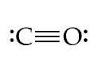
k. CN–
S17.3
a
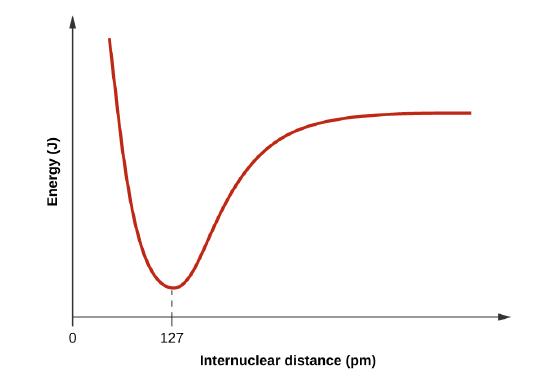
When H and Cl are separate (the x axis) the energy is at a particular value. As they approach, it decreases to a minimum at 127 pm (the bond distance), and then it increases sharply as you get closer.
You can also find the potential energy function of H-Cl and take the derivative with respect to internuclear distance and find minimum.
- \(H–Cl\): $$energy of one bond=431 kJ/mol /N_A=431 \times 10^3 J/mol x \dfrac{1 mol}{6.02 \times 10^{23} bonds}=7.16 \times 10^{-19} J/bond$$
S17.4
The single bond present in each molecule results from overlap of the relevant orbitals: F 2p orbitals in F2, the H 1s and F 2p orbitals in HF, and the Cl 3p orbital and Br 4p orbital in ClBr.
S17.5
\(\ce{H–C≡N}\) has two σ (H–C and C–N) and two π (making the CN triple bond).

S17.6
An ionic bond wave function takes into account the probability that the electrons of a multiatomic molecule might exist on the same atom; the covalent bond wave function assumes they exist on separate atoms.