Midterm 2 Solutions
- Page ID
- 50497
Problem 1 (2 points each = 20 points total)
MARK the following statements as TRUE or FALSE.
- The Pauli Exclusion Principle states that two or more electrons in a single atom must have the same four quantum numbers.
False
 At absolute zero, all intermolecular and intramolecular motion has ceased.
At absolute zero, all intermolecular and intramolecular motion has ceased.
False
 The square of the wavefunction is measure of the energy of the wavefunction.
The square of the wavefunction is measure of the energy of the wavefunction.
False
 The Bohr Principle states that an atom is wavelike only when it has enough mass to exceed the Bohr radius.
The Bohr Principle states that an atom is wavelike only when it has enough mass to exceed the Bohr radius.
False
 Amino acids are never part of the active site of an enzyme?
Amino acids are never part of the active site of an enzyme?
False
 The number of nodes in a wavefunction is typically correlated to the energy of that wavefunction.
The number of nodes in a wavefunction is typically correlated to the energy of that wavefunction.
True
 According to Einstein’s Law of photoelectron effect in a primary photoionization process of a metal, each electron is generated by the absorption of a single photon.
According to Einstein’s Law of photoelectron effect in a primary photoionization process of a metal, each electron is generated by the absorption of a single photon.
True
 Enzymes can make a reaction go faster by reducing DG for the reaction.
Enzymes can make a reaction go faster by reducing DG for the reaction.
False
 Hydrogen-like wavefunctions are derived from solving the Schrodinger equation for a charged nucleus with a single moving electron.
Hydrogen-like wavefunctions are derived from solving the Schrodinger equation for a charged nucleus with a single moving electron.
True
 The particle in the box model predicts that the particle has a small probability to be found outside the box as long as the potential walls surrounding the box are of finite height.
The particle in the box model predicts that the particle has a small probability to be found outside the box as long as the potential walls surrounding the box are of finite height.
True
Problem 2 (10+10=20 points)
2A) What is the energy of a particle with mass of 2.3 x 10-27 kg that is confined in a one-dimensional box of 50 Å length? Assume that the particle is in the third energy level.
\[E_3 = \frac{n^2h^2}{8mL^2} = \frac{9x(6.6x10^{-34}Js)^2}{8x(2.3x10^{-27}kg)(5x10^{-9}m)^2}\]
\[E_3 = 8.5x10^{-24}J\]
2B) What is the wavelength of a photon released during a transition from level three to level two in above system?
\[\Delta E = E_3 - E_2 = \frac{(n_3^2 - n_2^2)h^2}{8mL^2} = \frac{5x(6.6x10^{-34}Js)^2}{8x(2.3x10^{-27}kg)(5x10^{-9}m)^2}\]
\[\Delta E = 4.7x10^{-24}J\]
\[\Delta E = \frac{hc}{\lambda} = \frac{19.8x10^{-26}Jm}{4.7x10^{-24}J} = 4.2 cm\]
Problem 3 (10 + 5 points = 15 total)
3a) The speed of a hydrogen atom is 350 km s-1. If the uncertainty in its momentum is 0.01%, what is the uncertainty in its location? If a hydrogen atom has a diameter of 1.4 Å, how large is this uncertainty compared to its size (i.e., in percent?)
\[(\Delta x)(\Delta p) \geq \frac{\hbar}{2}\]
\[(\Delta x)(350000m/s)(1.673x10^{-27}) \geq 5.3x10^{-35}\]
\[\Delta x \geq 9x10^{-10}m\]
\[\frac{\Delta x}{x} = \frac{9}{1.4} = 6.43 = 643\%\]
Problem 5 (10 points each = 20 points)
B) A reaction that consume CO2 follows Michaelis-menten enzyme kinetics with Km=0.001 M, and the initial concentration of substrate=0.840 M. After 2 seconds, 5% of the substrate has been converted to product[DL1] . How much CO2 will be converted after 10 and 60 seconds?
Answer: 25% after 10 seconds and 100% after 60 seconds
Can either use standard MM equation
\[v_o= k_2[S]_o[E]_o/{[S]_o + K_m}\]
Or recognize that \([S]_o >> Km) so the system is running at V_max (full capacity). Therefor
\[V_max= k_2[E]_o\]
If 5% is consumed in 2 seconds, then 10 second will be 5x5=25%. All of it will be consumed by 60 seconds (by 40 second actually).
3B) When 2 x 10-10 mol is added to a 1-L solution containing its substrate at a concentration one hundred times the Km, it catalyzes the conversion of 75 µmol of substrate into product in three minutes. What is the enzyme’s turnover number (turnover rate)?
\[Kcat = Vmax / [E]_o\]
Because the velocity measured occurs far above Km, it represents Vmax.In three minutes, this amount of enzyme produced 75 µmol of product, equivalent to 25 x 10-6 mol of product per minute.The turnover number is, therefore, (25 x 10-6 mol/min)/(2 x 10-10 mol) = 12.5 x 104 min-1.
Problem 6 (2 + 5 = 8 points total)
Answer the following questions using the diagrams shown for enzymatic catalyzed reactions.
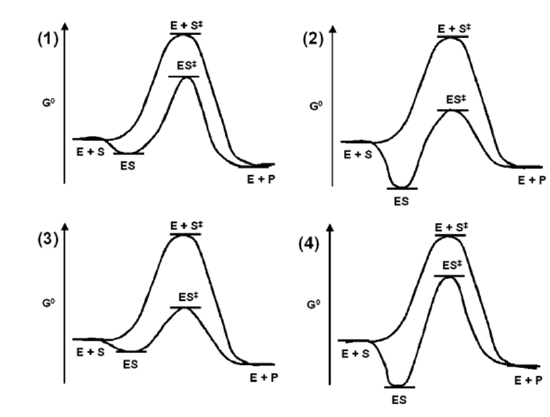
- Which enzyme is providing the least acceleration in relationship to the non-catalyzed reaction? 4
- Which enzyme is providing the greatest acceleration in relationship to the non-catalyzed reaction? 3
- When comparing enzymes 1 and 4, which will be faster? 1
- When comparing enzymes 2 and 3, which will be slower? 2
Problem 7 ( 6 + 3 + 3 = 12 points)
7A) How many electrons in a hydrogen atom can occupy the wavefunctions with the following values of l:
- l =0
1 orbital = 2 electrons
- l =3
7 orbitals = 14 electrons
- l =5
11 orbitals = 22 electrons
7B) What is the probability of finding a particle outside a box (choose either: 0, 1 or in-between)
- with finite potential walls and why?
In between, because the particle can tunneling through walls of finite height.
- with infinite potential walls and why?
Zero since the potential energy is infinite and a particle cannot have infinite energy
7C) What is the probability of finding a particle exactly in the middle of a box (with infinite potential walls) when excited to the n=1 state?
\[\int_{.5L+\epsilon}^{.5L-\epsilon}\frac{2}{L}sin(\frac{\pi x}{L})dx\]
Where after integration we take the limit as \(\epsilon\) goes to zero. For this problem we also accepted as correct:
1. 0 since finding a particle in an exact spot is impossible by the uncertainty principle
2. \[\int_{.5L}^{.5L}\frac{2}{L}sin(\frac{\pi x}{L})dx\]
3. \[\psi ^2 = \frac{2}{L}sin(\frac{\pi}{L}\frac{L}{2}) = \frac{2}{L}\]
Problem 8: 10 points
The diffraction phenomenon can be observed whenever the wavelength is comparable in magnitude to the size of a slit opening. How fast must your instructor, weighing 92 Kg, run to diffract through a door 1 m wide?
\[\lambda = \frac{h}{p} = \frac{h}{mv}\]
\[v = \frac{h}{\lambda m} = \frac{6.6x10^{-34}Js}{92kg} = 7.2x10^{-36}m/s\]

