7.6: Periodic Trends in the Size of Atoms and Effective Nuclear Charge
- Page ID
- 199831
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
- To understand periodic trends in atomic radii.
- To predict relative ionic sizes within an isoelectronic series.
Although some people fall into the trap of visualizing atoms and ions as small, hard spheres similar to miniature table-tennis balls or marbles, the quantum mechanical model tells us that their shapes and boundaries are much less definite than those images suggest. As a result, atoms and ions cannot be said to have exact sizes; however, some atoms are larger or smaller than others, and this influences their chemistry. In this section, we discuss how atomic and ion “sizes” are defined and obtained.
Atomic Radii
Recall that the probability of finding an electron in the various available orbitals falls off slowly as the distance from the nucleus increases. This point is illustrated in Figure \(\PageIndex{1}\) which shows a plot of total electron density for all occupied orbitals for three noble gases as a function of their distance from the nucleus. Electron density diminishes gradually with increasing distance, which makes it impossible to draw a sharp line marking the boundary of an atom.
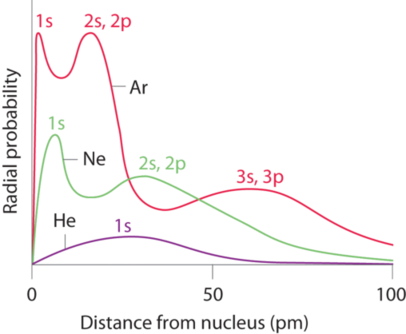
Figure \(\PageIndex{1}\) also shows that there are distinct peaks in the total electron density at particular distances and that these peaks occur at different distances from the nucleus for each element. Each peak in a given plot corresponds to the electron density in a given principal shell. Because helium has only one filled shell (n = 1), it shows only a single peak. In contrast, neon, with filled n = 1 and 2 principal shells, has two peaks. Argon, with filled n = 1, 2, and 3 principal shells, has three peaks. The peak for the filled n = 1 shell occurs at successively shorter distances for neon (Z = 10) and argon (Z = 18) because, with a greater number of protons, their nuclei are more positively charged than that of helium. Because the 1s2 shell is closest to the nucleus, its electrons are very poorly shielded by electrons in filled shells with larger values of n. Consequently, the two electrons in the n = 1 shell experience nearly the full nuclear charge, resulting in a strong electrostatic interaction between the electrons and the nucleus. The energy of the n = 1 shell also decreases tremendously (the filled 1s orbital becomes more stable) as the nuclear charge increases. For similar reasons, the filled n = 2 shell in argon is located closer to the nucleus and has a lower energy than the n = 2 shell in neon.
Figure \(\PageIndex{1}\) illustrates the difficulty of measuring the dimensions of an individual atom. Because distances between the nuclei in pairs of covalently bonded atoms can be measured quite precisely, however, chemists use these distances as a basis for describing the approximate sizes of atoms. For example, the internuclear distance in the diatomic Cl2 molecule is known to be 198 pm. We assign half of this distance to each chlorine atom, giving chlorine a covalent atomic radius (\(r_{cov}\)), which is half the distance between the nuclei of two like atoms joined by a covalent bond in the same molecule, of 99 pm or 0.99 Å (Figure \(\PageIndex{2a}\)). Atomic radii are often measured in angstroms (Å), a non-SI unit: 1 Å = 1 × 10−10 m = 100 pm.

In a similar approach, we can use the lengths of carbon–carbon single bonds in organic compounds, which are remarkably uniform at 154 pm, to assign a value of 77 pm as the covalent atomic radius for carbon. If these values do indeed reflect the actual sizes of the atoms, then we should be able to predict the lengths of covalent bonds formed between different elements by adding them. For example, we would predict a carbon–chlorine distance of 77 pm + 99 pm = 176 pm for a C–Cl bond, which is very close to the average value observed in many organochlorine compounds. A similar approach for measuring the size of ions is discussed later in this section.
Covalent atomic radii can be determined for most of the nonmetals, but how do chemists obtain atomic radii for elements that do not form covalent bonds? For these elements, a variety of other methods have been developed. With a metal, for example, the metallic atomic radius (\(r_{met}\)) is defined as half the distance between the nuclei of two adjacent metal atoms in the solid (Figure \(\PageIndex{2b}\)). For elements such as the noble gases, most of which form no stable compounds, we can use what is called the van der Waals atomic radius (\(r_{vdW}\)), which is half the internuclear distance between two nonbonded atoms in the solid (Figure \(\PageIndex{2c}\)). This is somewhat difficult for helium which does not form a solid at any temperature. An atom such as chlorine has both a covalent radius (the distance between the two atoms in a \(\ce{Cl2}\) molecule) and a van der Waals radius (the distance between two Cl atoms in different molecules in, for example, \(\ce{Cl2(s)}\) at low temperatures). These radii are generally not the same (Figure \(\PageIndex{2d}\)).
Periodic Trends in Atomic Radii
Because it is impossible to measure the sizes of both metallic and nonmetallic elements using any one method, chemists have developed a self-consistent way of calculating atomic radii using the quantum mechanical functions. Although the radii values obtained by such calculations are not identical to any of the experimentally measured sets of values, they do provide a way to compare the intrinsic sizes of all the elements and clearly show that atomic size varies in a periodic fashion (Figure \(\PageIndex{3}\)).
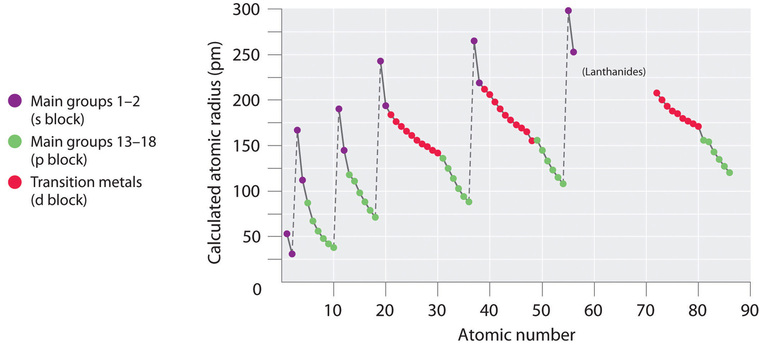
In the periodic table, atomic radii decrease from left to right across a row and increase from top to bottom down a column. Because of these two trends, the largest atoms are found in the lower left corner of the periodic table, and the smallest are found in the upper right corner (Figure \(\PageIndex{4}\)).
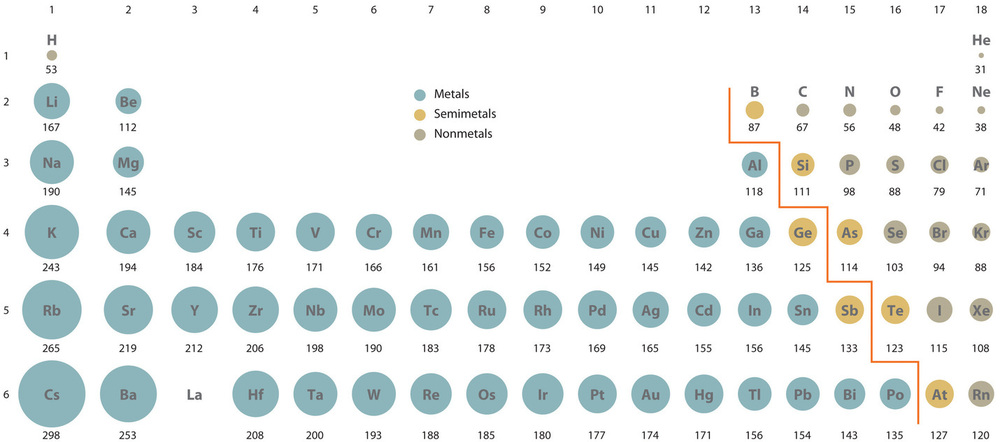
Trends in atomic size result from differences in the effective nuclear charges (\(Z_{eff}\)) experienced by electrons in the outermost orbitals of the elements. For all elements except H, the effective nuclear charge is always less than the actual nuclear charge because of shielding effects. The greater the effective nuclear charge, the more strongly the outermost electrons are attracted to the nucleus and the smaller the atomic radius.
Atomic radii decrease from left to right across a row and increase from top to bottom down a column.
The atoms in the second row of the periodic table (Li through Ne) illustrate the effect of electron shielding. All have a filled 1s2 inner shell, but as we go from left to right across the row, the nuclear charge increases from +3 to +10. Although electrons are being added to the 2s and 2p orbitals, electrons in the same principal shell are not very effective at shielding one another from the nuclear charge. Thus the single 2s electron in lithium experiences an effective nuclear charge of approximately +1 because the electrons in the filled 1s2 shell effectively neutralize two of the three positive charges in the nucleus. (More detailed calculations give a value of Zeff = +1.26 for Li.) In contrast, the two 2s electrons in beryllium do not shield each other very well, although the filled 1s2 shell effectively neutralizes two of the four positive charges in the nucleus. This means that the effective nuclear charge experienced by the 2s electrons in beryllium is between +1 and +2 (the calculated value is +1.66). Consequently, beryllium is significantly smaller than lithium. Similarly, as we proceed across the row, the increasing nuclear charge is not effectively neutralized by the electrons being added to the 2s and 2p orbitals. The result is a steady increase in the effective nuclear charge and a steady decrease in atomic size (Figure \(\PageIndex{5}\)).
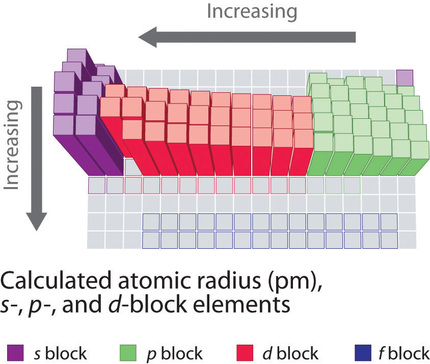
The increase in atomic size going down a column is also due to electron shielding, but the situation is more complex because the principal quantum number n is not constant. As we saw in Chapter 2, the size of the orbitals increases as n increases, provided the nuclear charge remains the same. In group 1, for example, the size of the atoms increases substantially going down the column. It may at first seem reasonable to attribute this effect to the successive addition of electrons to ns orbitals with increasing values of n. However, it is important to remember that the radius of an orbital depends dramatically on the nuclear charge. As we go down the column of the group 1 elements, the principal quantum number n increases from 2 to 6, but the nuclear charge increases from +3 to +55!
As a consequence the radii of the lower electron orbitals in Cesium are much smaller than those in lithium and the electrons in those orbitals experience a much larger force of attraction to the nucleus. That force depends on the effective nuclear charge experienced by the the inner electrons. If the outermost electrons in cesium experienced the full nuclear charge of +55, a cesium atom would be very small indeed. In fact, the effective nuclear charge felt by the outermost electrons in cesium is much less than expected (6 rather than 55). This means that cesium, with a 6s1 valence electron configuration, is much larger than lithium, with a 2s1 valence electron configuration. The effective nuclear charge changes relatively little for electrons in the outermost, or valence shell, from lithium to cesium because electrons in filled inner shells are highly effective at shielding electrons in outer shells from the nuclear charge. Even though cesium has a nuclear charge of +55, it has 54 electrons in its filled 1s22s22p63s23p64s23d104p65s24d105p6 shells, abbreviated as [Xe]5s24d105p6, which effectively neutralize most of the 55 positive charges in the nucleus. The same dynamic is responsible for the steady increase in size observed as we go down the other columns of the periodic table. Irregularities can usually be explained by variations in effective nuclear charge.
Electrons in the same principal shell are not very effective at shielding one another from the nuclear charge, whereas electrons in filled inner shells are highly effective at shielding electrons in outer shells from the nuclear charge.
On the basis of their positions in the periodic table, arrange these elements in order of increasing atomic radius: aluminum, carbon, and silicon.
Given: three elements
Asked for: arrange in order of increasing atomic radius
Strategy:
- Identify the location of the elements in the periodic table. Determine the relative sizes of elements located in the same column from their principal quantum number n. Then determine the order of elements in the same row from their effective nuclear charges. If the elements are not in the same column or row, use pairwise comparisons.
- List the elements in order of increasing atomic radius.
Solution:
A These elements are not all in the same column or row, so we must use pairwise comparisons. Carbon and silicon are both in group 14 with carbon lying above, so carbon is smaller than silicon (C < Si). Aluminum and silicon are both in the third row with aluminum lying to the left, so silicon is smaller than aluminum (Si < Al) because its effective nuclear charge is greater.
B Combining the two inequalities gives the overall order: C < Si < Al.
On the basis of their positions in the periodic table, arrange these elements in order of increasing size: oxygen, phosphorus, potassium, and sulfur.
- Answer
-
O < S < P < K
Atomic Radius: Atomic Radius, YouTube(opens in new window) [youtu.be]
Ionic Radii and Isoelectronic Series
An ion is formed when either one or more electrons are removed from a neutral atom to form a positive ion (cation) or when additional electrons attach themselves to neutral atoms to form a negative one (anion). The designations cation or anion come from the early experiments with electricity which found that positively charged particles were attracted to the negative pole of a battery, the cathode, while negatively charged ones were attracted to the positive pole, the anode.

Ionic compounds consist of regular repeating arrays of alternating positively charged cations and negatively charges anions. Although it is not possible to measure an ionic radius directly for the same reason it is not possible to directly measure an atom’s radius, it is possible to measure the distance between the nuclei of a cation and an adjacent anion in an ionic compound to determine the ionic radius (the radius of a cation or anion) of one or both. As illustrated in Figure \(\PageIndex{6}\), the internuclear distance corresponds to the sum of the radii of the cation and anion. A variety of methods have been developed to divide the experimentally measured distance proportionally between the smaller cation and larger anion. These methods produce sets of ionic radii that are internally consistent from one ionic compound to another, although each method gives slightly different values. For example, the radius of the Na+ ion is essentially the same in NaCl and Na2S, as long as the same method is used to measure it. Thus despite minor differences due to methodology, certain trends can be observed.
A comparison of ionic radii with atomic radii (Figure \(\PageIndex{7}\)) shows that a cation, having lost an electron, is always smaller than its parent neutral atom, and an anion, having gained an electron, is always larger than the parent neutral atom. When one or more electrons is removed from a neutral atom, two things happen: (1) repulsions between electrons in the same principal shell decrease because fewer electrons are present, and (2) the effective nuclear charge felt by the remaining electrons increases because there are fewer electrons to shield one another from the nucleus. Consequently, the size of the region of space occupied by electrons decreases and the ion shrinks (compare Li at 167 pm with Li+ at 76 pm). If different numbers of electrons can be removed to produce ions with different charges, the ion with the greatest positive charge is the smallest (compare Fe2+ at 78 pm with Fe3+ at 64.5 pm). Conversely, adding one or more electrons to a neutral atom causes electron–electron repulsions to increase and the effective nuclear charge to decrease, so the size of the probability region increases and the ion expands (compare F at 42 pm with F− at 133 pm).
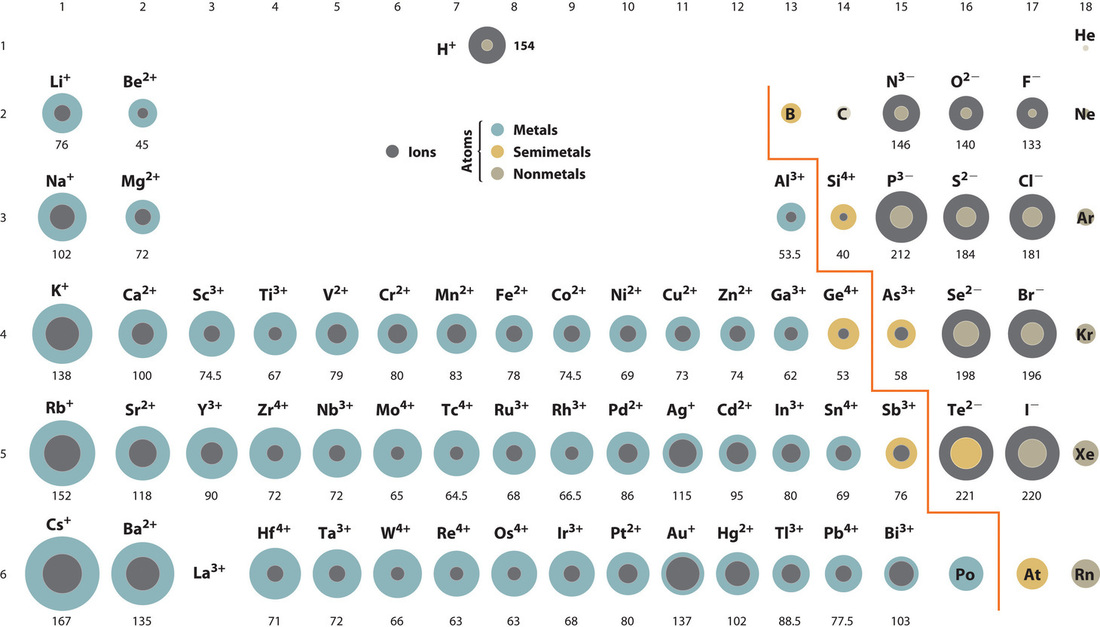
Cations are always smaller than the neutral atom and anions are always larger.
Because most elements form either a cation or an anion but not both, there are few opportunities to compare the sizes of a cation and an anion derived from the same neutral atom. A few compounds of sodium, however, contain the Na− ion, allowing comparison of its size with that of the far more familiar Na+ ion, which is found in many compounds. The radius of sodium in each of its three known oxidation states is given in Table \(\PageIndex{1}\). All three species have a nuclear charge of +11, but they contain 10 (Na+), 11 (Na0), and 12 (Na−) electrons. The Na+ ion is significantly smaller than the neutral Na atom because the 3s1 electron has been removed to give a closed shell with n = 2. The Na− ion is larger than the parent Na atom because the additional electron produces a 3s2 valence electron configuration, while the nuclear charge remains the same.
| Na+ | Na0 | Na− | |
|---|---|---|---|
| Electron Configuration | 1s22s22p6 | 1s22s22p63s1 | 1s22s22p63s2 |
| Radius (pm) | 102 | 154* | 202† |
| *The metallic radius measured for Na(s). †Source: M. J. Wagner and J. L. Dye, “Alkalides, Electrides, and Expanded Metals,” Annual Review of Materials Science 23 (1993): 225–253. | |||
Ionic radii follow the same vertical trend as atomic radii; that is, for ions with the same charge, the ionic radius increases going down a column. The reason is the same as for atomic radii: shielding by filled inner shells produces little change in the effective nuclear charge felt by the outermost electrons. Again, principal shells with larger values of n lie at successively greater distances from the nucleus.
Because elements in different columns tend to form ions with different charges, it is not possible to compare ions of the same charge across a row of the periodic table. Instead, elements that are next to each other tend to form ions with the same number of electrons but with different overall charges because of their different atomic numbers. Such a set of species is known as an isoelectronic series. For example, the isoelectronic series of species with the neon closed-shell configuration (1s22s22p6) is shown in Table \(\PageIndex{3}\).
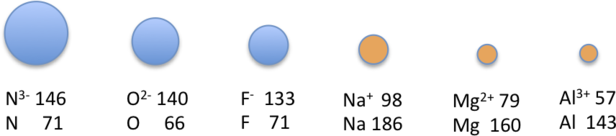
The sizes of the ions in this series decrease smoothly from N3− to Al3+. All six of the ions contain 10 electrons in the 1s, 2s, and 2p orbitals, but the nuclear charge varies from +7 (N) to +13 (Al). As the positive charge of the nucleus increases while the number of electrons remains the same, there is a greater electrostatic attraction between the electrons and the nucleus, which causes a decrease in radius. Consequently, the ion with the greatest nuclear charge (Al3+) is the smallest, and the ion with the smallest nuclear charge (N3−) is the largest. The neon atom in this isoelectronic series is not listed in Table \(\PageIndex{3}\), because neon forms no covalent or ionic compounds and hence its radius is difficult to measure.
| Ion | Radius (pm) | Atomic Number |
|---|---|---|
| N3− | 146 | 7 |
| O2− | 140 | 8 |
| F− | 133 | 9 |
| Na+ | 98 | 11 |
| Mg2+ | 79 | 12 |
| Al3+ | 57 | 13 |
Based on their positions in the periodic table, arrange these ions in order of increasing radius: Cl−, K+, S2−, and Se2−.
Given: four ions
Asked for: order by increasing radius
Strategy:
- Determine which ions form an isoelectronic series. Of those ions, predict their relative sizes based on their nuclear charges. For ions that do not form an isoelectronic series, locate their positions in the periodic table.
- Determine the relative sizes of the ions based on their principal quantum numbers n and their locations within a row.
Solution:
A We see that S and Cl are at the right of the third row, while K and Se are at the far left and right ends of the fourth row, respectively. K+, Cl−, and S2− form an isoelectronic series with the [Ar] closed-shell electron configuration; that is, all three ions contain 18 electrons but have different nuclear charges. Because K+ has the greatest nuclear charge (Z = 19), its radius is smallest, and S2− with Z = 16 has the largest radius. Because selenium is directly below sulfur, we expect the Se2− ion to be even larger than S2−.
B The order must therefore be K+ < Cl− < S2− < Se2−.
Based on their positions in the periodic table, arrange these ions in order of increasing size: Br−, Ca2+, Rb+, and Sr2+.
- Answer
-
Ca2+ < Sr2+ < Rb+ < Br−
Summary
Ionic radii share the same vertical trend as atomic radii, but the horizontal trends differ due to differences in ionic charges. A variety of methods have been established to measure the size of a single atom or ion. The covalent atomic radius (rcov) is half the internuclear distance in a molecule with two identical atoms bonded to each other, whereas the metallic atomic radius (rmet) is defined as half the distance between the nuclei of two adjacent atoms in a metallic element. The van der Waals radius (rvdW) of an element is half the internuclear distance between two nonbonded atoms in a solid. Atomic radii decrease from left to right across a row because of the increase in effective nuclear charge due to poor electron screening by other electrons in the same principal shell. Moreover, atomic radii increase from top to bottom down a column because the effective nuclear charge remains relatively constant as the principal quantum number increases. The ionic radii of cations and anions are always smaller or larger, respectively, than the parent atom due to changes in electron–electron repulsions, and the trends in ionic radius parallel those in atomic size. A comparison of the dimensions of atoms or ions that have the same number of electrons but different nuclear charges, called an isoelectronic series, shows a clear correlation between increasing nuclear charge and decreasing size.
Contributors and Attributions
Modified by Joshua Halpern (Howard University)
- To understand the basics of electron shielding and penetration
For an atom or an ion with only a single electron, we can calculate the potential energy by considering only the electrostatic attraction between the positively charged nucleus and the negatively charged electron. When more than one electron is present, however, the total energy of the atom or the ion depends not only on attractive electron-nucleus interactions but also on repulsive electron-electron interactions. When there are two electrons, the repulsive interactions depend on the positions of both electrons at a given instant, but because we cannot specify the exact positions of the electrons, it is impossible to exactly calculate the repulsive interactions. Consequently, we must use approximate methods to deal with the effect of electron-electron repulsions on orbital energies. These effects are the underlying basis for the periodic trends in elemental properties that we will explore in this chapter.
Electron Shielding and Effective Nuclear Charge
If an electron is far from the nucleus (i.e., if the distance \(r\) between the nucleus and the electron is large), then at any given moment, many of the other electrons will be between that electron and the nucleus (Figure \(\PageIndex{1}\)). Hence the electrons will cancel a portion of the positive charge of the nucleus and thereby decrease the attractive interaction between it and the electron farther away. As a result, the electron farther away experiences an effective nuclear charge (\(Z_{eff}\)) that is less than the actual nuclear charge \(Z\). This effect is called electron shielding.
As the distance between an electron and the nucleus approaches infinity, \(Z_{eff}\) approaches a value of 1 because all the other (\(Z − 1\)) electrons in the neutral atom are, on the average, between it and the nucleus. If, on the other hand, an electron is very close to the nucleus, then at any given moment most of the other electrons are farther from the nucleus and do not shield the nuclear charge. At \(r ≈ 0\), the positive charge experienced by an electron is approximately the full nuclear charge, or \(Z_{eff} ≈ Z\). At intermediate values of \(r\), the effective nuclear charge is somewhere between 1 and \(Z\):
\[1 ≤ Z_{eff} ≤ Z. \nonumber \]
Notice that \(Z_{eff} = Z\) only for hydrogen (Figure \(\PageIndex{2}\)).
Shielding refers to the core electrons repelling the outer electrons, which lowers the effective charge of the nucleus on the outer electrons. Hence, the nucleus has "less grip" on the outer electrons insofar as it is shielded from them.
\(Z_{eff}\) can be calculated by subtracting the magnitude of shielding from the total nuclear charge and the effective nuclear charge of an atom is given by the equation:
\[ Z_{eff}=Z-S \label{4} \]
where \(Z\) is the atomic number (number of protons in nucleus) and \(S\) is the shielding constant and is approximated by number of electrons between the nucleus and the electron in question (the number of nonvalence electrons). The value of \(Z_{eff}\) will provide information on how much of a charge an electron actually experiences.
We can see from Equation \ref{4} that the effective nuclear charge of an atom increases as the number of protons in an atom increases (Figure \(\PageIndex{2}\)). As we will discuss later on in the chapter, this phenomenon can explain the decrease in atomic radii we see as we go across the periodic table as electrons are held closer to the nucleus due to increase in number of protons and increase in effective nuclear charge.
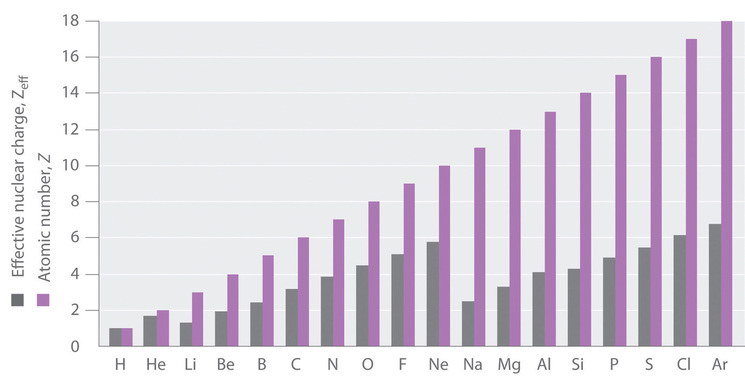
The shielding constant can be estimated by totaling the screening by all nonvalence electrons (\(n\)) except the one in question.
\[ S = \sum_{i}^{n-1} S_i \label{2.6.0} \]
where \(S_i\) is the shielding of the ith electron.
Electrons that are shielded from the full charge of the nucleus experience an effective nuclear charge (\(Z_{eff}\)) of the nucleus, which is some degree less than the full nuclear charge an electron would feel in a hydrogen atom or hydrogenlike ion.
From Equations \ref{4} and \ref{2.6.0}, \(Z_{eff}\) for a specific electron can be estimated is the shielding constants for that electron of all other electrons in species is known. A simple approximation is that all other non-valence electrons shield equally and fully:
\[S_i=1 \label{simple} \]
This crude approximation is demonstrated in Example \(\PageIndex{1}\).
What is the effective attraction \(Z_{eff}\) experienced by the valence electrons in the three isoelectronic species: the fluorine anion, the neutral neon atom, and sodium cation?
Solution
Each species has 10 electrons, and the number of nonvalence electrons is 2 (10 total electrons - 8 valence), but the effective nuclear charge varies because each has a different atomic number \(A\). This is an application of Equations \ref{4} and \ref{2.6.0}. We use the simple assumption that all electrons shield equally and fully the valence electrons (Equation \ref{simple}).
The charge \(Z\) of the nucleus of a fluorine atom is 9, but the valence electrons are screened appreciably by the core electrons (four electrons from the 1s and 2s orbitals) and partially by the 7 electrons in the 2p orbitals.
- \(Z_\mathrm{eff}(\mathrm{F}^-) = 9 - 2 = 7+\)
- \(Z_\mathrm{eff}(\mathrm{Ne}) = 10 - 2 = 8+\)
- \(Z_\mathrm{eff}(\mathrm{Na}^+) = 11 - 2 = 9+\)
So the sodium cation has the greatest effective nuclear charge. This also suggests that \(\mathrm{Na}^+\) has the smallest radius of these species and that is correct.
What is the effective attraction \(Z_{eff}\) experienced by the valence electrons in the magnesium anion, the neutral magnesium atom, and magnesium cation? Use the simple approximation for shielding constants. Compare your result for the magnesium atom to the more accurate value in Figure \(\PageIndex{2}\) and proposed an origin for the difference.
- Answer
-
- \(Z_\mathrm{eff}(\ce{Mg}^{-}) = 12 - 10 = 2+\)
- \(Z_\mathrm{eff}(\ce{Mg}) = 12 - 10 = 2+\)
- \(Z_\mathrm{eff}(\ce{Mg}^{+}) = 12 - 10 = 2+\)
Remember that the simple approximations in Equations \ref{2.6.0} and \ref{simple} suggest that valence electrons do not shield other valence electrons. Therefore, each of these species has the same number of non-valence electrons and Equation \ref{4} suggests the effective charge on each valence electron is identical for each of the three species.
This is not correct and a more complex model is needed to predict the experimental observed \(Z_{eff}\) value. The ability of valence electrons to shield other valence electrons or in partial amounts (e.g., \(S_i \neq 1\)) is in violation of Equations \ref{2.6.0} and \ref{simple}. That fact that these approximations are poor is suggested by the experimental \(Z_{eff}\) value shown in Figure \(\PageIndex{2}\) for \(\ce{Mg}\) of 3.2+. This is appreciably larger than the +2 estimated above, which means these simple approximations overestimate the total shielding constant \(S\). A more sophisticated model is needed.
Electron Penetration
The approximation in Equation \ref{simple} is a good first order description of electron shielding, but the actual \(Z_{eff}\) experienced by an electron in a given orbital depends not only on the spatial distribution of the electron in that orbital but also on the distribution of all the other electrons present. This leads to large differences in \(Z_{eff}\) for different elements, as shown in Figure \(\PageIndex{2}\) for the elements of the first three rows of the periodic table.
Penetration describes the proximity to which an electron can approach to the nucleus. In a multi-electron system, electron penetration is defined by an electron's relative electron density (probability density) near the nucleus of an atom (Figure \(\PageIndex{3}\)). Electrons in different orbitals have different electron densities around the nucleus. In other words, penetration depends on the shell (\(n\)) and subshell (\(l\)).
For example, a 1s electron (Figure \(\PageIndex{3}\); purple curve) has greater electron density near the nucleus than a 2p electron (Figure \(\PageIndex{3}\); red curve) and has a greater penetration. This related to the shielding constants since the 1s electrons are closer to the nucleus than a 2p electron, hence the 1s screens a 2p electron almost perfectly (\(S=1\). However, the 2s electron has a lower shielding constant (\(S<1\) because it can penetrate close to the nucleus in the small area of electron density within the first spherical node (Figure \(\PageIndex{3}\); green curve). In this way the 2s electron can "avoid" some of the shielding effect of the inner 1s electron.
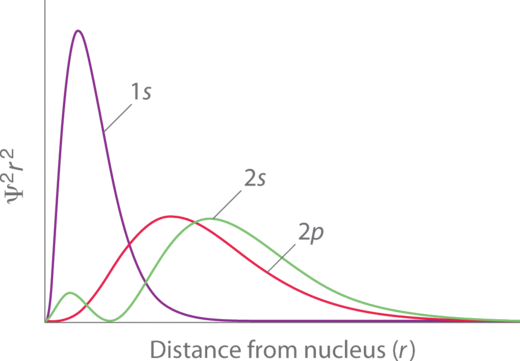
For the same shell value (\(n\)) the penetrating power of an electron follows this trend in subshells (Figure \(\PageIndex{3}\)):
\[s > p > d \approx f. \label{better1} \]
for different values of shell (n) and subshell (l), penetrating power of an electron follows this trend:
\[\ce{1s > 2s > 2p > 3s > 3p > 4s > 3d > 4p > 5s > 4d > 5p > 6s > 4f ...} \label{better2} \]
Penetration describes the proximity of electrons in an orbital to the nucleus. Electrons that have greater penetration can get closer to the nucleus and effectively block out the charge from electrons that have less proximity.
| Atom | Sublevel | Z | Zeff |
|---|---|---|---|
| H | 1s | 1 | 1 |
| He | 1s | 2 | 1.69 |
| Li | 1s, 2s | 3 | 2.69, 1.28 |
| Be | 1s, 2s | 4 | 3.68, 1.91 |
| B | 1s, 2s, 2p | 5 | 4.68, 2.58, 2.42 |
| F | 1s, 2s, 2p | 9 | 8.65, 5.13, 5.10 |
| Na | 1s, 2s, 2p, 3s | 11 | 10.63, 6.57, 6.80, 2.51 |
Data from E. Clementi and D. L. Raimondi; The Journal of Chemical Physics 38, 2686 (1963).
Because of the effects of shielding and the different radial distributions of orbitals with the same value of n but different values of l, the different subshells are not degenerate in a multielectron atom. For a given value of n, the ns orbital is always lower in energy than the np orbitals, which are lower in energy than the nd orbitals, and so forth. As a result, some subshells with higher principal quantum numbers are actually lower in energy than subshells with a lower value of n; for example, the 4s orbital is lower in energy than the 3d orbitals for most atoms.
The concepts of electron shielding, orbital penetration and effective nuclear charge were introduced above, but we did so in a qualitative manner (e.g., Equations \ref{better1} and \ref{better2}). A more accurate model for estimating electron shielding and corresponding effective nuclear charge experienced is Slater's Rules. However, the application of these rules is outside the scope of this text.
Zeff and Electron Shielding: Zeff and Electron Shielding(opens in new window) [youtu.be]
Summary
The calculation of orbital energies in atoms or ions with more than one electron (multielectron atoms or ions) is complicated by repulsive interactions between the electrons. The concept of electron shielding, in which intervening electrons act to reduce the positive nuclear charge experienced by an electron, allows the use of hydrogen-like orbitals and an effective nuclear charge (\(Z_{eff}\)) to describe electron distributions in more complex atoms or ions. The degree to which orbitals with different values of l and the same value of n overlap or penetrate filled inner shells results in slightly different energies for different subshells in the same principal shell in most atoms.

