5.6: Kinetic Molecular Theory
- Page ID
- 35369
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Skills to Develop
- To understand the five fundamentals of Kinetic Molecular Theory.
- To use Kinetic Molecular Theory to describe the behavior of the macroscopic gas laws.
The ideal gas equation
\[PV = nRT\]
describes how gases behave, e.g.:
- A gas expands when heated at constant pressure
- The pressure increases when a gas is compressed at constant temperature
However, the ideal gas law (nor any of the constituent gas laws) does not explain why gases behave this way? What happens to gas particles when conditions such as pressure and temperature change? This is addressed via Kinetic Molecule Theory.
The Fundamentals of Kinetic Molecular Theory (KMT)
The molecules of a gas are in a state of perpetual motion in which the velocity (that is, the speed and direction) of each molecule is completely random and independent of that of the other molecules. This fundamental assumption of the kinetic-molecular model helps us understand a wide range of commonly-observed phenomena. According to this model, most of the volume occupied by a gas is empty space; this is the main feature that distinguishes gases from condensed states of matter (liquids and solids) in which neighboring molecules are constantly in contact. Gas molecules are in rapid and continuous motion; at ordinary temperatures and pressures their velocities are of the order of 0.1-1 km/sec and each molecule experiences approximately 1010collisions with other molecules every second.
The five basic tenets of the kinetic-molecular theory are as follows:
- A gas is composed of molecules that are separated by average distances that are much greater than the sizes of the molecules themselves. The volume occupied by the molecules of the gas is negligible compared to the volume of the gas itself.
- The molecules of an ideal gas exert no attractive forces on each other, or on the walls of the container.
- The molecules are in constant random motion, and as material bodies, they obey Newton's laws of motion. This means that the molecules move in straight lines (see demo illustration at the left) until they collide with each other or with the walls of the container.
- Collisions are perfectly elastic; when two molecules collide, they change their directions and kinetic energies, but the total kinetic energy is conserved. Collisions are not “sticky".
- The average kinetic energy of the gas molecules is directly proportional to the absolute temperature. Notice that the term “average” is very important here; the velocities and kinetic energies of individual molecules will span a wide range of values, and some will even have zero velocity at a given instant. This implies that all molecular motion would cease if the temperature were reduced to absolute zero.
Note
The Kinetic-Molecular Theory is "the theory of moving molecules." -Rudolf Clausius, 1857
Pressure
If gases do in fact consist of widely-separated particles, then the observable properties of gases must be explainable in terms of the simple mechanics that govern the motions of the individual molecules. The kinetic molecular theory makes it easy to see why a gas should exert a pressure on the walls of a container. Any surface in contact with the gas is constantly bombarded by the molecules.
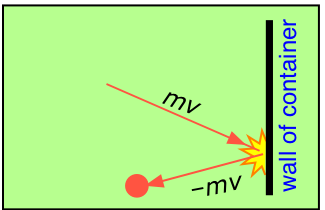
Figure 5.6.1: Pressure arises from the force due to the acceleration of molecules as they bound off a container's walls
At each collision, a molecule moving with momentum mv strikes the surface. Since the collisions are elastic, the molecule bounces back with the same velocity in the opposite direction. This change in velocity ΔV is equivalent to an acceleration \(a\); according to Newton's second law,
\[F = ma\]
with a force, \(F\), that is exerted on the surface of area \(A\) exerting a pressure
\[P = \dfrac{f}{A}\]
- The pressure of a gas is causes by collisions of the molecules with the walls of the container.
- The magnitude of the pressure is related to how hard and how often the molecules strike the wall
- The "hardness" of the impact of the molecules with the wall will be related to the velocity of the molecules times the mass of the molecules
Kinetic Interpretation of Absolute Temperature
According to the kinetic molecular theory, the average kinetic energy of an ideal gas is directly proportional to the absolute temperature. Kinetic energy is the energy a body has by virtue of its motion:
\[ KE = \dfrac{1}{2}m v^2\]
with
- \(KE\) is the kinetic energy of a molecule,
- \(m\) is the mass of the molecule, and
- \(v\) is the magnitude of the velocity of a molecule.
As the temperature of a gas rises, the average velocity of the molecules will increase; a doubling of the temperature will increase this velocity by a factor of four. Collisions with the walls of the container will transfer more momentum, and thus more kinetic energy, to the walls.

Figure 5.6.2: A microscopic picture of the molecules in a gas (balls) as a specific time. The magnitude of the velocity of each molecule is indicated by the length of the arrow.
If the walls are cooler than the gas, they will get warmer, returning less kinetic energy to the gas, and causing it to cool until thermal equilibrium is reached. Because temperature depends on the average kinetic energy, the concept of temperature only applies to a statistically meaningful sample of molecules. We will have more to say about molecular velocities and kinetic energies farther on.
Molecular Speed
Although the molecules in a sample of gas have an average kinetic energy (and therefore an average speed) the individual molecules move at various speeds. Some are moving fast, others relatively slowly
Figure 5.6.3: The distribution of speeds of nitrogen molecules at 0 °C and 100 °C.
At higher temperatures at greater fraction of the molecules are moving at higher speeds (Figure 3). What is the speed (velocity) of a molecule possessing average kinetic energy? KMT theory shows the the average kinetic energy (KE) is related to the root mean square (rms) speed \(u\)
\[KE = \dfrac{1}{2} m u^2\]
This is different from the typical definition of an average speed \( \langle v \rangle\) as demonstrated in Example 5.6.1.
Example 5.6.1
Suppose a gas consists of four molecules with speeds of 3.0, 4.5, 5.2 and 8.3 m/s. What is the difference between the average speed and root mean square speed of this gas?
SOLUTION
The average speed is:
\[ \langle v \rangle = \dfrac{3.0 + 4.5 + 5.2 + 8.3}{4}=5.25 \; m/s\]
The root mean square speed is:
\[u= \sqrt{\dfrac{3.0^2+ 4.5^2+5.2^2+8.3^2}{4}}= 5.59 \; m/s\]
The Gas Laws Explained from a KMT Perspective
-
Kinetic explanation of Boyle's law: Boyle's law is easily explained by the kinetic molecular theory. The pressure of a gas depends on the number of times per second that the molecules strike the surface of the container. If we compress the gas to a smaller volume, the same number of molecules are now acting against a smaller surface area, so the number striking per unit of area, and thus the pressure, is now greater.
-
Kinetic explanation of Charles' law: Kinetic molecular theory states that an increase in temperature raises the average kinetic energy of the molecules. If the molecules are moving more rapidly but the pressure remains the same, then the molecules must stay farther apart, so that the increase in the rate at which molecules collide with the surface of the container is compensated for by a corresponding increase in the area of this surface as the gas expands.
-
Kinetic explanation of Avogadro's law: If we increase the number of gas molecules in a closed container, more of them will collide with the walls per unit time. If the pressure is to remain constant, the volume must increase in proportion, so that the molecules strike the walls less frequently, and over a larger surface area.
-
Kinetic explanation of Dalton's law: "Every gas is a vacuum to every other gas". This is the way Dalton stated what we now know as his law of partial pressures. It simply means that each gas present in a mixture of gases acts independently of the others. This makes sense because of first fundamental tenet of KMT theory is that gas molecules have negligible volumes. So Gas A in mixture of A and B acts as if Gas B were not there at all. Each contributes its own pressure to the total pressure within the container, in proportion to the fraction of the molecules it represents
Note
- The absolute temperature is a measure of the average kinetic energy of its molecules
- If two different gases are at the same temperature, their molecules have the same average kinetic energy
- If the temperature of a gas is doubled, the average kinetic energy of its molecules is doubled
Contributors
Mike Blaber (Florida State University)
Stephen Lower, Professor Emeritus (Simon Fraser U.) Chem1 Virtual Textbook

