6.2: The Mole
- Last updated
- Save as PDF
- Page ID
- 241566
Learning Objectives
- To define the mole unit.
Figure \(\PageIndex{1}\) shows that we need 2 hydrogen atoms and 1 oxygen atom to make 1 water molecule. If we want to make 2 water molecules, we will need 4 hydrogen atoms and 2 oxygen atoms. If we want to make 5 molecules of water, we need 10 hydrogen atoms and 5 oxygen atoms. The ratio of atoms we will need to make any number of water molecules is the same: 2 hydrogen atoms to 1 oxygen atom.

One problem we have, however, is that it is extremely difficult, if not impossible, to organize atoms one at a time. As stated in the introduction, we deal with billions of atoms at a time. How can we keep track of so many atoms (and molecules) at a time? We do it by using mass rather than by counting individual atoms.
A hydrogen atom has a mass of approximately 1 u. An oxygen atom has a mass of approximately 16 u. The ratio of the mass of an oxygen atom to the mass of a hydrogen atom is therefore approximately 16:1.
If we have 2 atoms of each element, the ratio of their masses is approximately 32:2, which reduces to 16:1—the same ratio. If we have 12 atoms of each element, the ratio of their total masses is approximately (12 × 16):(12 × 1), or 192:12, which also reduces to 16:1. If we have 100 atoms of each element, the ratio of the masses is approximately 1,600:100, which again reduces to 16:1. As long as we have equal numbers of hydrogen and oxygen atoms, the ratio of the masses will always be 16:1.
The same consistency is seen when ratios of the masses of other elements are compared. For example, the ratio of the masses of silicon atoms to equal numbers of hydrogen atoms is always approximately 28:1, while the ratio of the masses of calcium atoms to equal numbers of lithium atoms is approximately 40:7.
So we have established that the masses of atoms are constant with respect to each other, as long as we have the same number of each type of atom. Consider a more macroscopic example. If a sample contains 40 g of Ca, this sample has the same number of atoms as there are in a sample of 7 g of Li. What we need, then, is a number that represents a convenient quantity of atoms so we can relate macroscopic quantities of substances. Clearly even 12 atoms are too few because atoms themselves are so small. We need a number that represents billions and billions of atoms.
Chemists use the term mole to represent a large number of atoms or molecules. Just as a dozen implies 12 things, a mole (abbreviated as mol) represents 6.022 × 1023 things. The number 6.022 × 1023, called Avogadro’s number after the 19th-century chemist Amedeo Avogadro, is the number we use in chemistry to represent macroscopic amounts of atoms and molecules. Thus, if we have 6.022 × 1023 Na atoms, we say we have 1 mol of Na atoms. If we have 2 mol of Na atoms, we have 2 × (6.022 × 1023) Na atoms, or 1.2044 × 1024 Na atoms. Similarly, if we have 0.5 mol of benzene (C6H6) molecules, we have 0.5 × (6.022 × 1023) C6H6 molecules, or 3.011 × 1023 C6H6 molecules.
A mole represents a very large number! If 1 mol of quarters were stacked in a column, it could stretch back and forth between Earth and the sun 6.8 billion times.
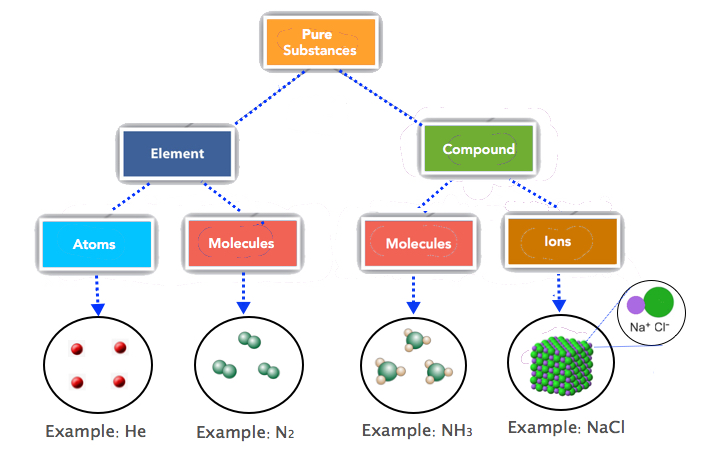
Notice that we are applying the mole unit to different types of chemical entities. The word mole represents a number of things—6.022 × 1023 of them—but does not by itself specify what “they” are. The chemical entities can be atoms, molecules, formula units and ions. This specific information needs to be specified accurately. Most students find this confusing hence, we need to review the composition of elements, covalent and ionic compounds.
Most elements are made up of individual atoms, such as helium. However, some elements consist of molecules, such as the diatomic elements, nitrogen, hydrogen, oxygen, etc. One mole of He consists of 6.022 × 1023 He atoms but one mole of nitrogen contains 6.022 × 1023 N2 molecules. The basic units of covalent (molecular) compounds are molecules as well. The molecules of "compounds" consist of different kinds of atoms while the molecules of "elements" consist of only one type of atom. For example, the molecules of ammonia (NH3) consist of nitrogen and hydrogen atoms while N2 molecules have N atoms only. Compounds that are ionic, like NaCl, are represented by ionic formulas. One mole of NaCl, for example, refers to 6.022 × 1023 formula units of NaCl. And, one formula unit of NaCl consists of one sodium ion and one chloride ion. Figure 6.1.2 summarizes the basic units of elements, covalent and ionic compounds
Conversion Between Moles and Atoms, Molecules and Ions
Using our unit conversion techniques learned in Chapter 1, we can use the mole relationship and the chemical formula to convert back and forth between the moles and the number of chemical entities (atoms, molecules or ions).
Because 1 N2 molecule contains 2 N atoms, 1 mol of N2 molecules (6.022 × 1023 molecules) has 2 mol of N atoms. Using formulas to indicate how many atoms of each element we have in a substance, we can relate the number of moles of molecules to the number of moles of atoms. For example, in 1 mol of ethanol (C2H6O), we can construct the following relationships (Table \(\PageIndex{1}\)):
| 1 Molecule of \(C_2H_6O\) Has | 1 Mol of \(C_2H_6O\) Has | Molecular Relationships |
|---|---|---|
| 2 C atoms | 2 mol of C atoms | \(\mathrm{\dfrac{2\: mol\: C\: atoms}{1\: mol\: C_2H_6O\: molecules}}\) or \(\mathrm{\dfrac{1\: mol\: C_2H_6O\: molecules}{2\: mol\: C\: atoms}}\) |
| 6 H atoms | 6 mol of H atoms | \(\mathrm{\dfrac{6\: mol\: H\: atoms}{1\: mol\: C_2H_6O\: molecules}}\) or \(\mathrm{\dfrac{1\: mol\: C_2H_6O\: molecules}{6\: mol\: H\: atoms}}\) |
| 1 O atom | 1 mol of O atoms | \(\mathrm{\dfrac{1\: mol\: O\: atoms}{1\: mol\: C_2H_6O\: molecules}}\) or \(\mathrm{\dfrac{1\: mol\: C_2H_6O\: molecules}{1\: mol\: O\: atoms}}\) |
The following example illustrates how we can use these relationships as conversion factors.
Example \(\PageIndex{1}\)
If a sample consists of 2.5 mol of ethanol (C2H6O), how many moles of carbon atoms, hydrogen atoms, and oxygen atoms does it have?
Solution
Using the relationships in Table \(\PageIndex{1}\), we apply the appropriate conversion factor for each element:
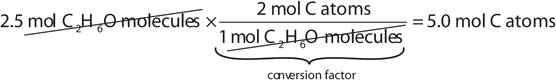
Note how the unit mol C2H6O molecules cancels algebraically. Similar equations can be constructed for determining the number of H and O atoms:
\(\mathrm{2.5\: mol\: C_2H_6O\: molecules\times\dfrac{6\: mol\: H\: atoms}{1\: mol\: C_2H_6O\: molecules}=15\: mol\: H\: atoms}\)
\(\mathrm{2.5\: mol\: C_2H_6O\: molecules\times\dfrac{1\: mol\: O\: atoms}{1\: mol\: C_2H_6O\: molecules}=2.5\: mol\: O\: atoms}\)
Exercise \(\PageIndex{1}\)
If a sample contains 6.75 mol of Na2SO4, how many moles of sodium atoms, sulfur atoms, and oxygen atoms does it have?
- Answer
-
13.5 mol Na, 6.75 mol S and 27 mol O.
We can use Avogadro's number as a conversion factor, or ratio, in dimensional analysis problems. For example, if we are dealing with element X, the mole relationship is expressed as follows:
\[\text{1 mol X} = 6.022 \times 10^{23} \text{ X atoms} \nonumber \]
We can convert this relationship into two possible conversion factors shown below:
\(\mathrm{\dfrac{1\: mol\: X\: }{6.022\times 10^{23}\: X\: atoms}}\) or \(\mathrm{\dfrac{6.022\times 10^{23}\: X\: atoms}{1\: mol\: X\: }}\)
If the number of "atoms of element X" is given, we can convert it into "moles of X" by multiplying the given value with the conversion factor at the left. However, if the number of "mol of X" is given, the appropriate conversion factor to use is the one at the right.
If we are dealing with a molecular compound (such as C4H10), the mole relationship is expressed as follows:
\[\text{1 mol C4H10} = 6.022 \times 10^{23} \text{ C4H10 molecules} \nonumber \]
If working with ionic compounds (such as NaCl), the mole relationship is expressed as follows:
\[\text{1 mol NaCl} = 6.022 \times 10^{23} \text{ NaCl formula units} \nonumber \]
Example \(\PageIndex{2}\)
How many formula units are present in 2.34 mol of NaCl? How many ions are in 2.34 mol?
Solution
Typically in a problem like this, we start with what we are given and apply the appropriate conversion factor. Here, we are given a quantity of 2.34 mol of NaCl, to which we can apply the definition of a mole as a conversion factor:
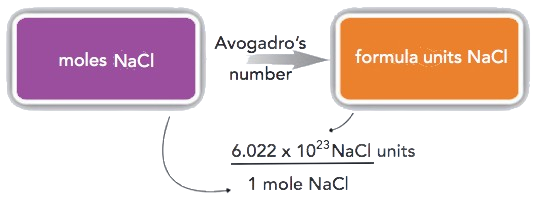
\(\mathrm{2.34\: mol\: NaCl\times\dfrac{6.022\times10^{23}\: NaCl\: units}{1\: mol\: NaCl}=1.41\times10^{24}\: NaCl\: units}\)
Because there are two ions per formula unit, there are
\(\mathrm{1.41\times10^{24}\: NaCl\: units\times\dfrac{2\: ions}{NaCl\: units}=2.82\times10^{24}\: ions}\)
in the sample.
Exercise \(\PageIndex{2}\)
How many molecules are present in 16.02 mol of C4H10? How many atoms are in 16.02 mol?
- Answer
-
9.647 x 1024molecules, 1.351 x 1026 atoms.
Key Takeaway
- A mole is 6.022 × 1023 things.

