1.17: Nano-Particles and Quantum Dots
- Page ID
- 73009
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)CHEM 174 Physical Chemistry Laboratory II
Nano-Particles, Quantum Dots and Emission Spectroscopy
Introduction
Nano-technology is the science and engineering of devices with a size range between 1 to 100 nm. Substances in this size range may have properties that are different than those in the bulk. For example the semiconductor cadmium phosphide in the bulk is black but smaller particles can be red, orange, yellow or white depending upon their size (Brown et al., 2009). The smallest particles are white.
Quantum dots are very small aggregates of semiconductor material that contain 103 to 105 atoms and are between 1 to 10 nm in diameter. For quantum dots prepared from a given substance, their color and electrical properties can be tuned by varying their size. They have potential applications in biology and medicine, photovoltaic electricity generation, light sources and display devices and computing. Their applications to biological problems are among the most significant. Organic dyes have a long history of applications to problems in microscopy, analysis and the treatment of disease. Quantum dots can be engineered to specifications much more precisely than traditional organic dyes. They provide a very intense light when excited and they are very stable, they may persist for months in a biological system. Applications include, tagging of cells and their real-time observation of cells over long time periods, in-vitro imaging of cells (Dahan et al. 2003; Ballou et al., 2004) and the delivery of gene-silencing molecules into cells (Newswise, 2008). The latter is an example of a potential therapeutic application of quantum dots. The major potential drawbacks are toxicity and other environmental effects that are not yet well known.
Semiconductors
Covalent bonds are formed from the overlap of atomic orbitals. When the bonds are formed both bonding and anti-bonding molecular orbitals are formed. For every bonding molecular orbital there is an anti-bonding molecular orbital formed. When a p-orbital overlaps with another p-orbital three bonding molecular orbital and three anti-bonding molecular orbitals are formed. In a crystal the bonding molecular orbitals constitute the valence band and anti-bonding orbitals constitute the conduction band. The difference in energy between the valence band and the conduction band is called the band gap, Figure 1.
In metals the band gap is very low and there is a population of electrons in the conduction band. These are the electrons that conduct electricity. The band gap is greater in semiconductors and few electrons are found in the conduction band. The absorption of a photon may promote an electron from the valence band to the conduction band. This excitation of the electron from the valence band creates “hole” in the valence band. Conversely the recombination of an electron and a hole may result in light emission; this is the basis of the light-emitting diode, Figure 2.
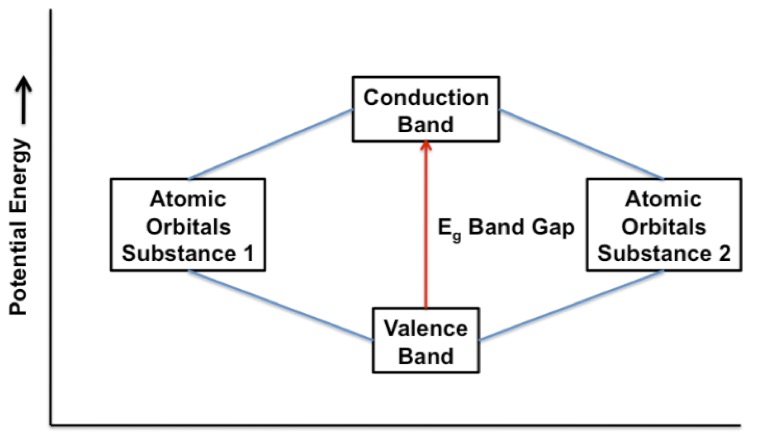
Figure 1. The figure shows the formation of bonding (valence band) and anti-bonding molecular orbitals (conduction band) from atomic orbitals. The band gap is the potential energy difference between the valence and conduction band.
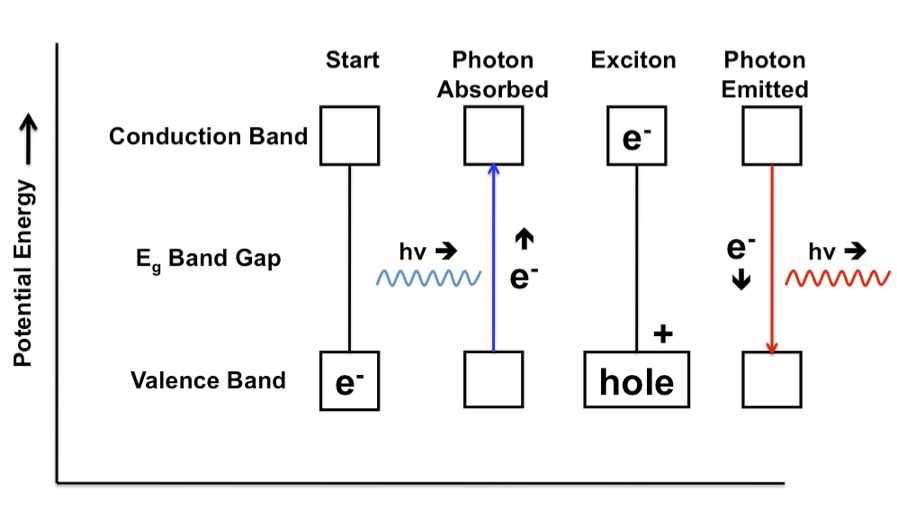
Figure 2. An electron is initially in the ground state. Next a photon with energy at least equal to the band gap is absorbed and the electron is promoted from the valence band to the conduction bond. A hole is left behind. (Note that while there is a net positive charge left behind, it is not correct to call the hole positive.) The electron and hole pair together is called an exciton. Finally the electron will return to valence band and a photon is emitted.
Quantum Mechanics
In the laboratory “Dye Color, the Particle in a Box and Determination of the Length of a Molecular System,” the quantum mechanics of a particle in a linear box was presented. Schrödinger’s equation in one dimension is Equation (1)
\[\widehat{H} \psi = E \psi \nonumber \] \[-\frac{\hbar^{2} }{2m}\frac{\partial ^{2}}{\partial x ^{2}}+ V\left ( x \right ) \nonumber \] where: \(\widehat{H}\) is the Hamiltonian, \(\psi \) is the wavefunction, \( E \) represents the possible energy levels, \(\hbar \) is Planck’s constant, \( h \), divided by \( 2 \pi \), \( m \) is the particle’s mass, \(\ x \) is the spatial dimension and \( V\left ( x \right ) \) is the potential energy.
For the particle in a box of length, \( L \), the boundary conditions are \( V\left ( 0 \right ) = + \infty \), \( V\left ( L \right ) = + \infty \) and \( V\left ( x \right ) = 0 \) for \( 0 < x < L \). Solution of Equation (1) for these boundary conditions yields the energy levels given by Equation (2).
\[E = n^{2} \frac{h^{2}}{8mL^{2}} \nonumber \] \[n=1,2,3... \nonumber \]
where: \( n \) are integers (quantum numbers).
The particle in a box can be extended to a three-dimensional sphere. The Hamiltonian for a spherical particle in a box is given by Equation (3). \[\widehat{H} = -\frac{\hbar^{2} }{2m} \nabla^{^{2}} \nonumber \]
In spherical coordinates the boundary condition is \( V\left ( r \right ) = 0 \) for \( 0 \leq r < R \) and \( V(r) = + \infty \) for \( r \geq R \) where: \( R \) is the radius of a sphere. The energy levels of a spherical particle in a box are given by Equation (4). \[ E = n^{2} \frac{h^{2}}{8mR^{2}} \nonumber \] \[ n=1,2,3... \nonumber \]
The approximate Hamiltonian for an exciton is similar to that for the spherical particle in a box but both the electron and the hole are confined within the quantum dot. In addition there is an electrostatic interaction between the electron and the hole that follows Coulomb’s Law (Atkins and de Paula, 2006). \[ \widehat{H} = -\frac{ \hbar^{2}}{2m_{e}} \nabla_{e}^{2} -\frac{ \hbar^{2}}{2m_{h}} \nabla_{h}^{2}-\frac{e^{2}}{4\pi \varepsilon \left | r_{e} - r_{h} \right |} \nonumber \]
where: \( m_{e} \) is the mass of the electron, \( m_{h} \) is the mass of the hole, \( e \) is the charge of an electron, \( \varepsilon \) is the permittivity of the semiconductor and \( \left | r_{e} - r_{h} \right | \) is the absolute value of the distance between the electron and the hole. The boundary conditions for exciton are the same as for the spherical particle in a box. The solution for the energy of an exciton, \( E_{ex} \), is given by the following equation, (Atkins and de Paula, 2006).
\[ E_{ex} = \frac{h^{2}}{8R^{2}}\left ( \frac{1}{m_{e}} - \frac{1}{m_{h}}\right ) - \frac{1.8 e^{2}}{4\pi \epsilon R} \nonumber \] The band gap energy, \( E_{g} \), is:
\[ E_{g} = - \frac{1.8 e^{2}}{4\pi \epsilon R} \nonumber \]
\[ E_{g} = \frac{{E}'}{R} \nonumber \] where \[ {E}' = - \frac{1.8 e^{2}}{4 \pi \epsilon} \nonumber \]
\[ E_{ex} = \frac{h^{2}}{8R^{2}}\left ( \frac{1}{m_{e}} - \frac{1}{m_{h}}\right ) + \frac{{E}'}{ R} \nonumber \]
Exciton Creation and Emission
In this experiment quantum dots will be excited by blue light photons, emitted from a diode source, to form excitons. The excitons decay and when the electron recombines with the hole a photon with energy equal to \( E_{ex} \) is emitted. If the wavelength of the emitted photon is measured the radius of the quantum dot can be calculated starting with Equation (9) and Equation (10).
\[ E=\frac{hc}{\lambda } \nonumber \]
Equating Equations (9) and (10) yields the following Equation (11).
\[ \frac{hc}{\lambda } = \frac{h^{2}}{8R^{2}}\left ( \frac{1}{m_{e}} - \frac{1}{m_{h}}\right ) - \frac{{E}'}{R} \nonumber \]
To determine the radius of the quantum dot from the wavelength of the exciton emission, multiply each term in Equation (11) by R2 and rearrange to a quadratic form that may be solved by using the quadratic equation.
\[ \frac{hcR^{2}}{\lambda } - {E}'R - \frac{h^{2}}{8}\left ( \frac{1}{m_{e}} - \frac{1}{m_{h}}\right ) = 0 \nonumber \]
Let:
\[ a = \frac{hcR^{2}}{\lambda } \nonumber \] \[ b = - {E}'R \nonumber \] \[ c = - \frac{h^{2}}{8}\left ( \frac{1}{m_{e}} - \frac{1}{m_{h}}\right ) \nonumber \]
Then:
\[ R = \frac{- b \pm \sqrt{b^{2}-4ac}}{2a} \nonumber \] or \[ R =\lambda \times \left ( \frac{ {E}' + \sqrt{{E}'^{2} + \frac{h^{3} c }{2 \lambda }\left ( \frac{1}{m_{e}} - \frac{1}{m_{h}}\right ) }}{2hc} \right ) \nonumber \]
You may want to check the derivation of the final expression from the quadratic equation.
In your calculations use the following values:
| Quantity | Value |
| h | 6.626 × 10-34 J s |
| c | 2.998 × 10+8 m s-1 |
| me | 9.109 × 10-31 kg |
| mh | 6.830 × 10-30 kg |
| E’ | 8.750 × 10-28 J m |
Procedure
Required Equipment
Quantum dots (Four different sizes are provided in vials of solution).
Ocean Optics UV-Vis Spectrometer
Red and Blue Light Emitting Diodes
Backlight for Absorption Measurements
You will measure both absorption spectra and emission spectra of the quantum dots. You will use the emission spectra to calculate the radii of the four different sizes of quantum dots.
Absorption Spectra
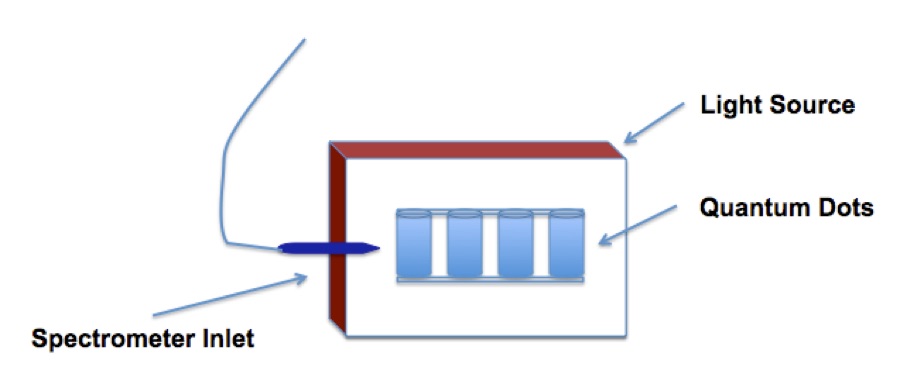
- Use the Ocean Optics spectrometer to take a background spectrum of the background light source, Figure 3.
- Place the vials containing the quantum dots in front of the background light source.
- Use the Ocean Optics spectrometer to record a spectrum of each vial.
- For your report plot the spectra for each vial as absorption spectra \( A = \ln \left ( \frac{I_{o}}{I} \right ) \). Use the background spectrum as your Io.
Emission Spectra
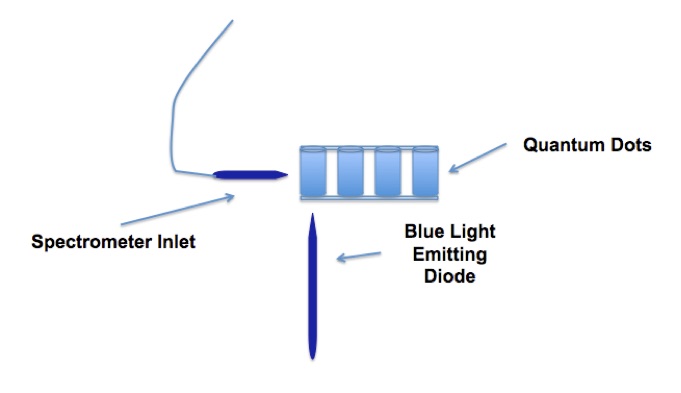
- Use a blue light emitting diode to excite the quantum dots. Use the Ocean Optics spectrometer to take a spectrum of the blue light emitting diode. Do not point the diode directly into the spectrometer optical fiber. Rather reflect the light in to the spectrometer by using a white surface such as a piece of paper.
- Place the blue light emitting diode below a vial and turn it on, Figure 4.
- Use the Ocean Optics spectrometer to record an emission spectrum of the vial.
- Repeat steps 3 and 4 until you have done all four vials.
Calculations, Questions and Report
Use your wavelength calibration curve to determine the calibrated wavelength scale for all of your measured spectra. This includes the absorption spectra, the light emitting diode spectrum and the exciton emission data. For the absorption spectra and the exciton spectra you can label these according to their trace color seen in the vials.
Use the background spectrum and the four spectra obtained under the section “Absorption Spectra” to calculate the absorption spectrum for each vial of quantum dots. Plot the absorbance spectrum for each of the vials of quantum dots using the calibrated wavelength scale and include in your report.
For the data obtained under the section “Emission Spectra” first make a plot of the emission spectrum of the blue light emitting diode using the calibrated wavelength scale. Plot the emission spectrum for each of the vials of quantum dots of quantum dots using the calibrated wavelength scale and include in your report.
For the exciton emission spectra, find the wavelength of the maximum emission for each of the vials. Use Equation (14) to calculate the radius of the four sizes of quantum dots. Summarize your results in a Table such as the following.
| Solution Color | Peak Wavelength (nm) | Radius (nm) |
| Color | ###.# | #.### |
Make a plot of quantum dot radius (y-axis) as a function of the peak wavelength of the emitted light (x-axis).
In the discussion and conclusions section consider the following. (1) What happens to the wavelength of light emitted as the radius of the quantum dot increases? (2) Examine the absorption spectra. From the absorption spectra discuss why a blue light emitting diode creates an exciton and why the red light emitting diode does not for the quantum dots used in this experiment.
References
Atkins, P. and J. de Paula, “Atkin’s Physical Chemistry, 8th Edition”, Freeman, New York, 2006.
Ballou, B., B.C. Lagerholm, L.A. Ernst, M.P. Bruchez, A.S. Waggoner, Noninvasive imaging of quantum dots in mice, Bioconjugate Chemistry, 15, 79-86, 2004.
Brown, T.L., H.E., LeMay, Jr., B.E Bursten and C.J. Murphy, “Chemistry the Central Science,” Pearson Prentice Hall, New Jersey, 2009.
Dahan, M., S. Levi, C. Luccardini, P. Rostaing, B. Riveau, A. Triller, Diffusion dynamics of glycine receptors revealed by single-quantum dot tracking, Science, 302, 442-445, 2003.
Newswise, Gene Silencer and Quantum Dots Reduce Protein Production to a Whisper, http://newswise.com/articles/view/542018/, Retrieved on June 24, 2008.

