1.13: Particle in a Box
- Page ID
- 72194
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)CHEM 174 Physical Chemistry Laboratory II
Dye Color, the Particle in a Box and
Determination of the Length of a Molecular System
Purpose
The objectives of this experiment include:
• Learning more about how organic compounds absorb radiation.
• Why compounds have color.
• How spectroscopic measurements may be used to derive some molecular properties (in this case the length of a conjugated pi-bonded system in dye molecules).
Introduction
White light is a mixture of all wavelengths of the visible spectrum. Color results when a compound absorbs light in a portion of the visible spectrum and transmits (or reflects) the remainder. Absorption of blue light produces the color red while the absorption of red light produces the color blue-green. Therefore to understand how organic dyes produce color it is necessary to understand how these compounds absorb light.
Consider the following series of cyanine dyes (I- is not shown in each case below):
1,1'-Diethyl-2,2'-cyanine iodide – (Dye A)
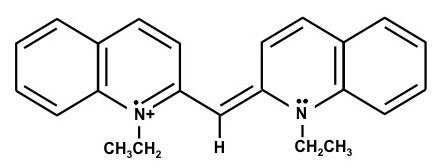
1,1'-Diethyl-2,2'-carbocyanine iodide – (Dye B)
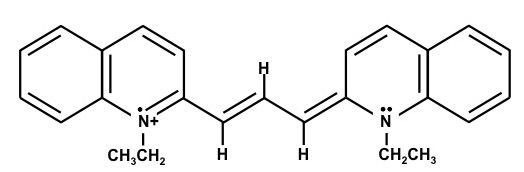
1,1'-Diethyl-2,2'-dicarbocyanine iodide – (Dye C)
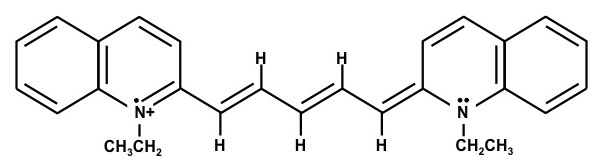
1,1'-Diethyl-4,4'-cyanine iodide – (Dye D)
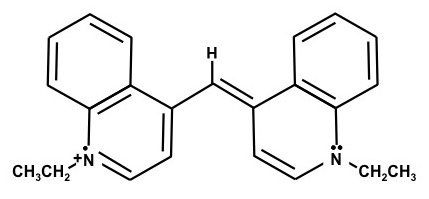
1,1'-Diethyl-4,4'carbocyanine iodide – (Dye E)
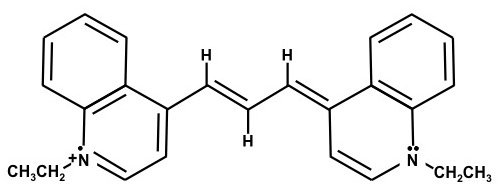
1,1'-Diethyl-4,4'-dicarbocyanine iodide – (Dye F)
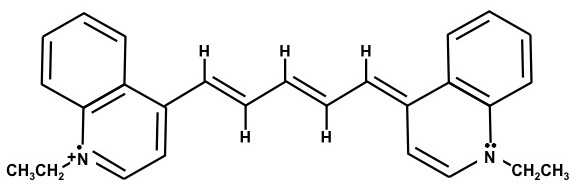
The chemical structures are resonance structures; the positive charge can be equally well represented as residing on either nitrogen atom. In reality the pi electrons may be considered to reside across the system of conjugated pi-bond system that extends from one nitrogen atom to the other, Figure 1. The conjugated pi-bonded system extends above and below the plane of the sigma bonds.
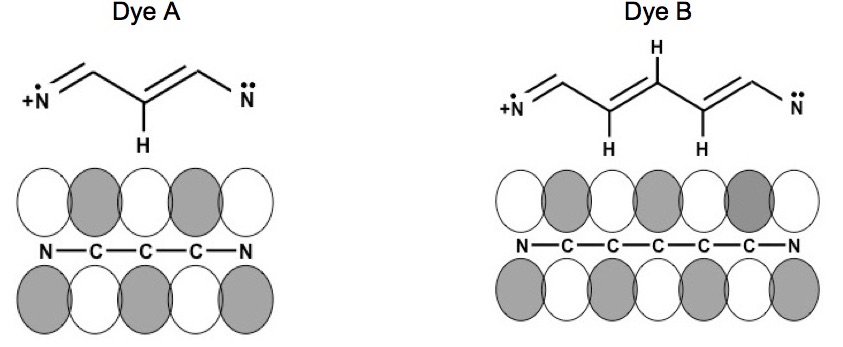
Figure 1. Conjugated pi-bonded system for dyes A and B.
Electrons change energy levels when radiation is absorbed. Schrödinger’s equation is used to calculate the energy levels, Equation (1).
\[-\frac{\hbar^{2} }{2m}\frac{\partial ^{2}\psi}{\partial x ^{2}}+ V\left ( x \right ) \psi = E \psi \nonumber \]
where: \(\hbar\)is Planck’s constant divided by 2π , \(m\) is the particle’s mass, \( V\left ( x \right )\) is the system’s potential energy, \( \psi \) is the wave function and \( E \) represents the possible energy levels.
The potential energy of a system needs to be defined to calculate the energy levels. Figure 2 shows the potential energy of the conjugated pi-bonded systems for dyes A and B. Figure 2 shows that there is a potential energy barrier at the nitrogen atoms and there are “wells” at each atom; however to a reasonable degree of accuracy the potential energy of the conjugated pi-bonded system can be approximated by a particle in a box potential.
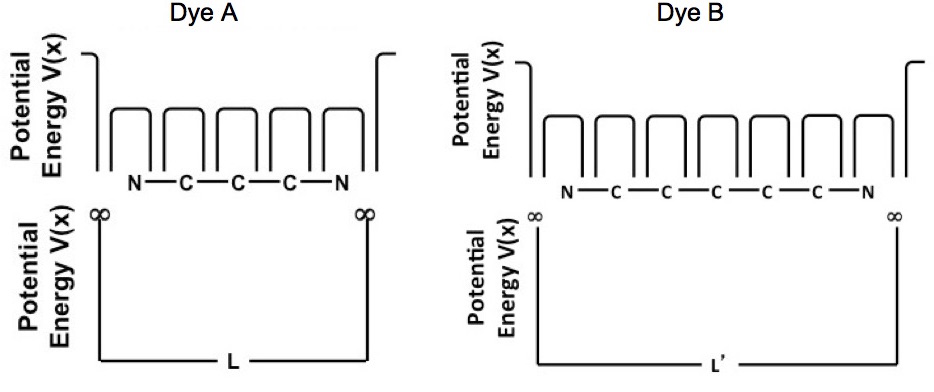
Figure 2. Potential energy of the conjugated pi-bond system for dyes A and B.
The solution of Schrödinger’s equation for the particle in a box yields the energy levels given by Equation (2).
\[E = n^{2} \frac{h^{2}}{8mL^{2}} \nonumber \] \[n=1,2,3... \nonumber \]
where: \( E \) represents the possible energy levels \( h \) is Planck’s constant, \( m \) is the particle’s mass and \( L \) is the length of the box.
Pauli Exclusion Principle and Packing Electrons into the Particle in a Box
Dye A has 6 electrons and dye B has 8 electrons in their respective pi-bond systems. If the particle in a box is used to represent these molecules then the pi electrons need to be distributed into the box. The Pauli exclusion principle and the energy levels establish the electron distribution.
An electron is a fermion and the Pauli Principle states that the total wave function for a system of fermions must be antisymmetric when particles are interchanged. Suppose the total wave function is ψ(q1,q2,q3,...) where q1,q2,q3,... are the coordinates / quantum numbers of electrons 1, 2, 3,… If electrons 1 and 2 are exchanged:
\[\psi \left ( q_{1}, q_{2}, q_{3}, q_{4}, ... \right ) = - \psi \left ( q_{2}, q_{1}, q_{3}, q_{4}, ... \right ) \nonumber \]
Suppose there were two electrons with the same set of quantum numbers (q1), then the total wave function would be ψ(q1,q1,q3,...). If the two electrons with the same set of quantum numbers were switched then Equation (4) results.
\[\psi \left ( q_{1}, q_{1}, q_{3}, q_{4}, ... \right ) = - \psi \left ( q_{1}, q_{1}, q_{3}, q_{4}, ... \right ) \nonumber \]
For any function, f(x), if f(x) = -f(x) then f(x) must be equal to zero. If ψ(q1,q1,q3,...) is equal to zero then probability of any two electrons having the same identical set of quantum numbers is zero.
In the case of electrons in the particle in a box there are two quantum numbers, n and spin. The quantum number n = 1, 2, 3… and the spin of an electron can be either up (+1/2) or down (-1/2). So each level of the particle in a box can contain two electrons, one spin up and the other spin down. Figure 3 shows how pi electrons for dye A (a 6 electron system) and dye B (a 8 electron system) are contained in the box when it is in the ground state. Note that the energy levels are more closely spaced due to the fact that dye B is represented by a larger box.
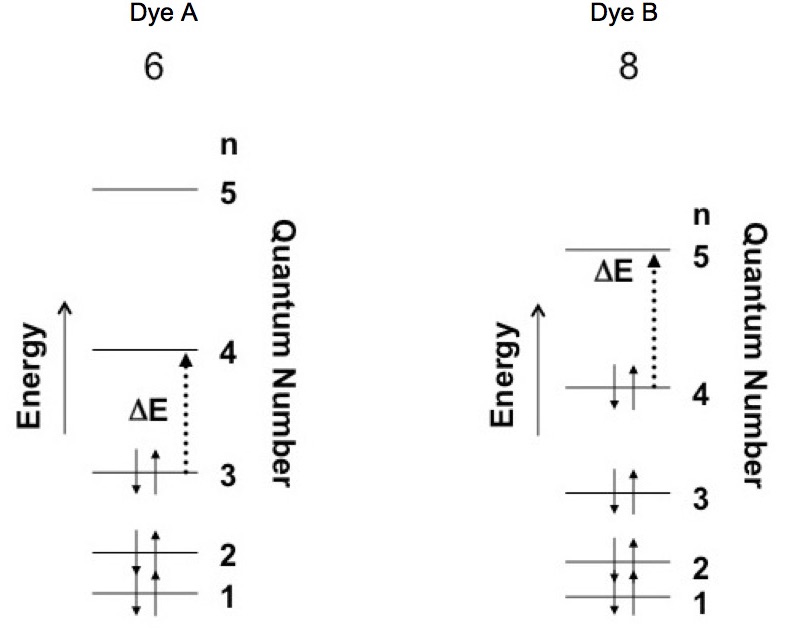
Figure 3. Assignment of electrons into particle in a box model for dyes A and B. The figure also shows the change in state caused by the absorption of a photon.
Dye A Dye B
Absorption of Energy
The change in energy associated with an electron jumping from one state to another is given by equation (5).
\[ \Delta E = \frac{h^{2}}{8mL^{2}} \left ( n_{f}^{2} - n_{i}^{2} \right ) \nonumber \]
where: ΔE is the change in energy, h is Planck’s constant, m is the mass of the electron, L is the length of the box and ni and nf are the initial and final quantum numbers.
Three things need to be considered to calculate the energy changes from Equation 5. For the dyes studied in this experiment the number of electrons (N) is an even number, p. There will be two electrons per energy level because of the Pauli Exclusion Principle. The principle quantum number changes by +1. Mathematically:
Equations (6 - 9)
\[p=n_{i}=\frac{N}{2} \nonumber \] \[ n_{f}=n_{i}+1 \nonumber \] \[ \Delta E = \frac{h^{2}}{8mL^{2}} \left [ \left ( p + 1 \right )^{2} - p^{2}\right ] \nonumber \] \[ \Delta E = \frac{h^{2}}{8mL^{2}} \left ( 2p+1 \right ) \nonumber \]
Remembering that:
\[ \lambda _{abs} = \frac{hc}{\Delta E} \nonumber \]
where λabs is the wavelength of the absorbed radiation and c is the speed of light, the following equations result.
\[ \lambda _{abs} = \frac{8mL^{2}c}{h\left ( 2p+1 \right )} \nonumber \] or Equation (11) \[ L=\sqrt{\frac{\lambda _{abs}h\left ( 2p +1 \right )}{8mc}} \nonumber \]
In the experiment the length of the conjugated pi-system will be calculated for each dye from measurements of λabs and Equation (11).
Safety
All six dyes: 1,1'-Diethyl-4,4'-cyanine iodide, 1,1'-Diethyl-4,4'-carbocyanine iodide, 1,1'-Diethyl4,4'-dicarbocyanine iodide, 1,1'-Diethyl-2,2'-cyanine iodide, 1,1'-Diethyl-2,2'-carbocyanine iodide and 1,1'-Diethyl-2,2'-dicarbocyanine iodide and methanol are considered highly toxic and irritate the skin. Do not get the dye solutions or methanol on your skin or in your eyes. Wear eye protection.
Procedure
- Solutions of dyes A – F in methanol have been prepared.
Note: In the following work completely clean the cuvette between samples. Use the same spectrometer settings and the same cuvette for the background and the dye solutions. Also do not cross contaminate the dye solutions by the using same pipette to transfer different dye solutions.
- Fill a cuvette with methanol and record a spectrum. This spectrum will be your background spectrum (Io) for this dye.
- Add a drop or two dye A solution. You should just be able to see a little color.
- Wash the cuvette. Go back to step 3
- Repeat steps 3 – 5 until spectra have been recorded for all the dye solutions.
Calculations
- Calculate absorbance spectra for the dye solutions by taking the natural log of the ratio between the background spectra and the dye solutions.
\[ A = \ln \left ( \frac{I_{o}}{I} \right ) \nonumber \]
- Correct the wavelength scale using the calibrations given in the class handout.
- Make plots of the absorbance spectra for dyes A – F. You may combine the plots in one or two page graphs.
Fill out the worksheet given below as you do the following.
- Identify the color of each dye.
- Identify the wavelength of the maximum absorbance, λmax, for each dye.
- Count the number of pi-electrons, N.
- Calculate the length of the conjugated pi-system, L, for each of the dyes from the measured λmax and Equation (11). Provide a sample calculation in your report.
- Count the number of bonds in the conjugated pi-system for each dye.
- Assume that each bond has a length of 0.139 nm and estimate the length of the box from the number of bonds. Provide a sample calculation in your report
- Evaluate and tabulate the difference between the length of the box calculated from Equation (11) and the length estimated from the number of bonds for each dye.
Report and Questions
- For the recalibration include a plot of the known wavelengths as a function of the measured wavelengths and the linear fit with your report.
- Discuss the observed colors and the absorption spectra. What is the relationship between the dye colors and the spectra?
- Make two plots of λmax as a function of the length of the box calculated from Equation (11): one plot for dyes A – C and another for D – F.
- Discuss the difference between the length of the box calculated from Equation (11) and the length estimated from the number of bonds. Is the difference usually positive or negative? Suggest reasons for this difference.
Reference
McRae, E.G. and M. Kasha (1958). J. Chem. Phys. 28, 721.
Pope, M., C.E. Swenberg, Electronic Processes in Organic Crystals, (Oxford University Press, New York, 1982), Chapter 1D.
New Mexico State University, Department of Chemistry
http://www.chemistry.nmsu.edu/studntres/chem435/Lab5/
_________________________________________________________________________________________________
Worksheet for particle in a box; include with your report.
Name_________________________________
| Dye | Color | λmax(nm) | Number of pi- electrons N | Experimental box length (nm) |
Number of bonds in conjugated system | Predicted box length (nm) |
Difference Experimental – Predicted (nm) |
| A | |||||||
| B | |||||||
| C | |||||||
| D | |||||||
| E | |||||||
| F |

