9.2: Standard Reduction Potentials
- Page ID
- 142293
Skills to Develop
- To use redox potentials to predict whether a reaction is spontaneous.
- To balance redox reactions using half-reactions.
In a galvanic cell, current is produced when electrons flow externally through the circuit from the anode to the cathode because of a difference in potential energy between the two electrodes in the electrochemical cell. In the Zn/Cu system, the valence electrons in zinc have a substantially higher potential energy than the valence electrons in copper because of shielding of the s electrons of zinc by the electrons in filled d orbitals. Hence electrons flow spontaneously from zinc to copper(II) ions, forming zinc(II) ions and metallic copper. Just like water flowing spontaneously downhill, which can be made to do work by forcing a waterwheel, the flow of electrons from a higher potential energy to a lower one can also be harnessed to perform work.

Figure \(\PageIndex{1}\): Potential Energy Difference in the Zn/Cu System. The potential energy of a system consisting of metallic \(Zn\) and aqueous Cu2+ ions is greater than the potential energy of a system consisting of metallic Cu and aqueous \(Zn^{2+}\) ions. Much of this potential energy difference is because the valence electrons of metallic Zn are higher in energy than the valence electrons of metallic Cu. Because the Zn(s) + Cu2+(aq) system is higher in energy by 1.10 V than the Cu(s) + Zn2+(aq) system, energy is released when electrons are transferred from Zn to Cu2+ to form Cu and Zn2+.
Because the potential energy of valence electrons differs greatly from one substance to another, the voltage of a galvanic cell depends partly on the identity of the reacting substances. If we construct a galvanic cell similar to the one in part (a) in Figure \(\PageIndex{1}\) but instead of copper use a strip of cobalt metal and 1 M Co2+ in the cathode compartment, the measured voltage is not 1.10 V but 0.51 V. Thus we can conclude that the difference in potential energy between the valence electrons of cobalt and zinc is less than the difference between the valence electrons of copper and zinc by 0.59 V.
The measured potential of a cell also depends strongly on the concentrations of the reacting species and the temperature of the system. To develop a scale of relative potentials that will allow us to predict the direction of an electrochemical reaction and the magnitude of the driving force for the reaction, the potentials for oxidations and reductions of different substances must be measured under comparable conditions. To do this, chemists use the standard cell potential (E°cell), defined as the potential of a cell measured under standard conditions—that is, with all species in their standard states (1 M for solutions, concentrated solutions of salts (about 1 M) generally do not exhibit ideal behavior, and the actual standard state corresponds to an activity of 1 rather than a concentration of 1 M. Corrections for non ideal behavior are important for precise quantitative work but not for the more qualitative approach that we are taking here. 1 atm for gases, pure solids or pure liquids for other substances) and at a fixed temperature, usually 25°C.
Measured redox potentials depend on the potential energy of valence electrons, the concentrations of the species in the reaction, and the temperature of the system.
Measuring Standard Electrode Potentials
It is physically impossible to measure the potential of a single electrode: only the difference between the potentials of two electrodes can be measured (this is analogous to measuring absolute enthalpies or free energies). Recall that only differences in enthalpy and free energy can be measured.) We can, however, compare the standard cell potentials for two different galvanic cells that have one kind of electrode in common. This allows us to measure the potential difference between two dissimilar electrodes. For example, the measured standard cell potential (E°) for the Zn/Cu system is 1.10 V, whereas E° for the corresponding Zn/Co system is 0.51 V. This implies that the potential difference between the Co and Cu electrodes is 1.10 V − 0.51 V = 0.59 V. In fact, that is exactly the potential measured under standard conditions if a cell is constructed with the following cell diagram:
\[Co_{(s)} ∣ Co^{2+}(aq, 1 M)∥Cu^{2+}(aq, 1 M) ∣ Cu (s)\;\;\; E°=0.59\; V \label{20.4.1}\]
This cell diagram corresponds to the oxidation of a cobalt anode and the reduction of Cu2+ in solution at the copper cathode.
All tabulated values of standard electrode potentials by convention are listed for a reaction written as a reduction, not as an oxidation, to be able to compare standard potentials for different substances (Table P1). The standard cell potential (E°cell) is therefore the difference between the tabulated reduction potentials of the two half-reactions, not their sum:
\[E°_{cell} = E°_{cathode} − E°_{anode} \label{20.4.2}\]
In contrast, recall that half-reactions are written to show the reduction and oxidation reactions that actually occur in the cell, so the overall cell reaction is written as the sum of the two half-reactions. According to Equation \(\ref{20.4.2}\), when we know the standard potential for any single half-reaction, we can obtain the value of the standard potential of many other half-reactions by measuring the standard potential of the corresponding cell.
The overall cell reaction is the sum of the two half-reactions, but the cell potential is the difference between the reduction potentials:
\[E°_{cell} = E°_{cathode} − E°_{anode}\]
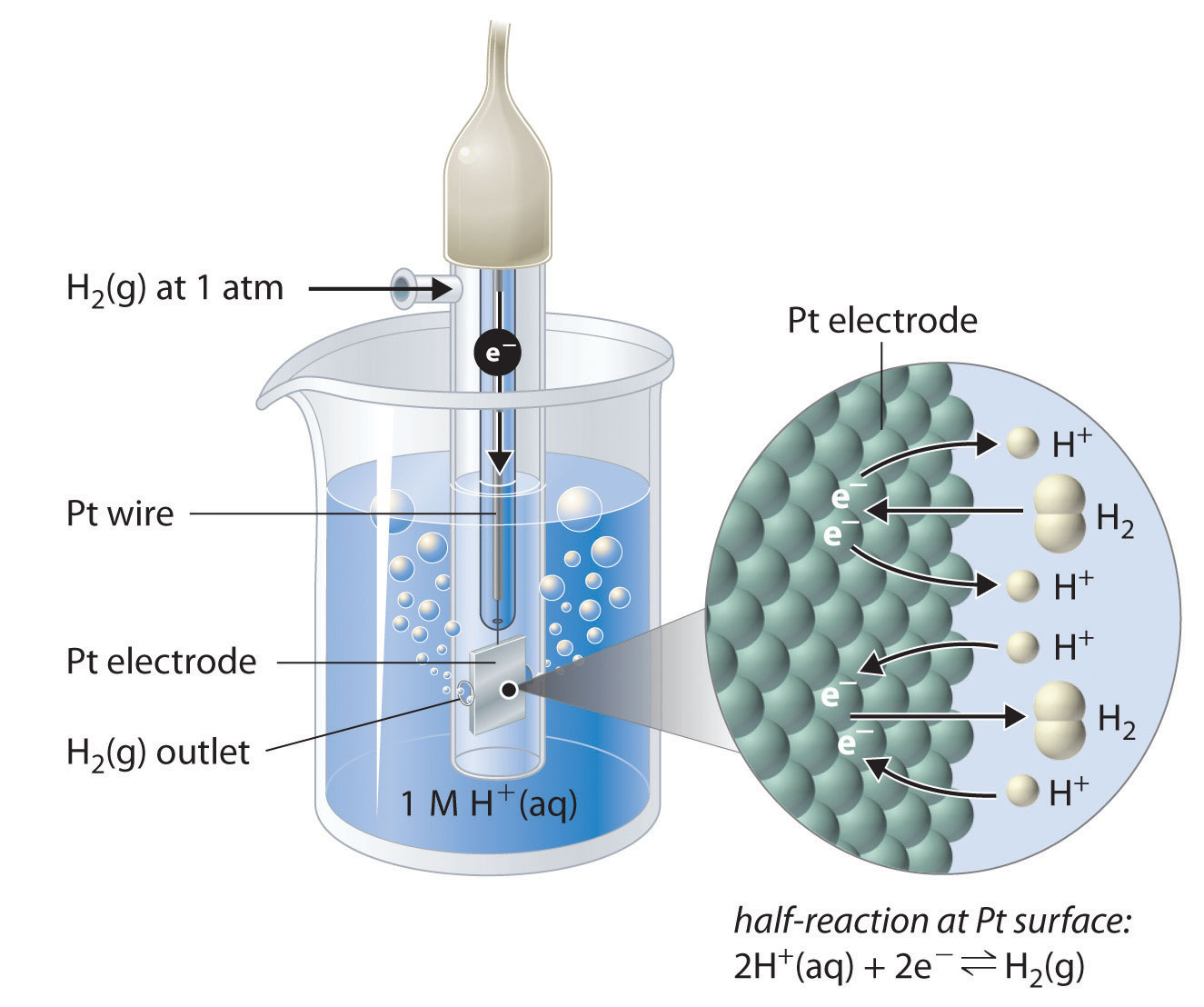
Figure \(\PageIndex{2}\): The Standard Hydrogen Electrode. The SHE consists of platinum wire that is connected to a Pt surface in contact with an aqueous solution containing 1 M H+ in equilibrium with H2 gas at a pressure of 1 atm. In the molecular view, the Pt surface catalyzes the oxidation of hydrogen molecules to protons or the reduction of protons to hydrogen gas. (Water is omitted for clarity.) The standard potential of the SHE is arbitrarily assigned a value of 0 V.
Although it is impossible to measure the potential of any electrode directly, we can choose a reference electrode whose potential is defined as 0 V under standard conditions. The standard hydrogen electrode (SHE) is universally used for this purpose and is assigned a standard potential of 0 V. It consists of a strip of platinum wire in contact with an aqueous solution containing 1 M H+. The [H+] in solution is in equilibrium with H2 gas at a pressure of 1 atm at the Pt-solution interface (Figure \(\PageIndex{2}\)). Protons are reduced or hydrogen molecules are oxidized at the Pt surface according to the following equation:
\[2H^+_{(aq)}+2e^− \rightleftharpoons H_{2(g)} \label{20.4.3}\]
One especially attractive feature of the SHE is that the Pt metal electrode is not consumed during the reaction.

Figure \(\PageIndex{3}\): Determining a Standard Electrode Potential Using a Standard Hydrogen Electrode. The voltmeter shows that the standard cell potential of a galvanic cell consisting of a SHE and a Zn/Zn2+ couple is \(E°_{cell}\) = 0.76 V. Because the zinc electrode in this cell dissolves spontaneously to form Zn2+(aq) ions while H+(aq) ions are reduced to H2 at the platinum surface, the standard electrode potential of the Zn2+/Zn couple is −0.76 V.
Figure \(\PageIndex{3}\) shows a galvanic cell that consists of a SHE in one beaker and a Zn strip in another beaker containing a solution of Zn2+ ions. When the circuit is closed, the voltmeter indicates a potential of 0.76 V. The zinc electrode begins to dissolve to form Zn2+, and H+ ions are reduced to H2 in the other compartment. Thus the hydrogen electrode is the cathode, and the zinc electrode is the anode. The diagram for this galvanic cell is as follows:
\[Zn_{(s)}∣Zn^{2+}_{(aq)}∥H^+(aq, 1 M)∣H_2(g, 1 atm)∣Pt_{(s)} \label{20.4.4}\]
The half-reactions that actually occur in the cell and their corresponding electrode potentials are as follows:
- cathode: \[2H^+_{(aq)} + 2e^− \rightarrow H_{2(g)}\;\;\; E°_{cathode}=0 V \label{20.4.5}\]
- anode: \[Zn_{(s)} \rightarrow Zn^{2+}_{(aq)}+2e^−\;\;\; E°_{anode}=−0.76\; V \label{20.4.6}\]
- overall: \[Zn_{(s)}+2H^+_{(aq)} \rightarrow Zn^{2+}_{(aq)}+H_{2(g)} \label{20.4.7}\]
Although the reaction at the anode is an oxidation, by convention its tabulated E° value is reported as a reduction potential. The potential of a half-reaction measured against the SHE under standard conditions is called the standard electrode potential for that half-reaction.In this example, the standard reduction potential for Zn2+(aq) + 2e− → Zn(s) is −0.76 V, which means that the standard electrode potential for the reaction that occurs at the anode, the oxidation of Zn to Zn2+, often called the Zn/Zn2+ redox couple, or the Zn/Zn2+ couple, is −(−0.76 V) = 0.76 V. We must therefore subtract E°anode from E°cathode to obtain
\[E°_{cell}: 0 \,V − (−0.76\, V) = 0.76\, V\]
Because electrical potential is the energy needed to move a charged particle in an electric field, standard electrode potentials for half-reactions are intensive properties and do not depend on the amount of substance involved. Consequently, E° values are independent of the stoichiometric coefficients for the half-reaction, and, most important, the coefficients used to produce a balanced overall reaction do not affect the value of the cell potential.
E° values do NOT depend on the stoichiometric coefficients for a half-reaction, because it is an intensive property.
Standard Electrode Potentials
To measure the potential of the Cu/Cu2+ couple, we can construct a galvanic cell analogous to the one shown in Figure \(\PageIndex{3}\) but containing a Cu/Cu2+ couple in the sample compartment instead of Zn/Zn2+. When we close the circuit this time, the measured potential for the cell is negative (−0.34 V) rather than positive. The negative value of \(E°_{cell}\) indicates that the direction of spontaneous electron flow is the opposite of that for the Zn/Zn2+ couple. Hence the reactions that occur spontaneously, indicated by a positive \(E°_{cell}\), are the reduction of Cu2+ to Cu at the copper electrode. The copper electrode gains mass as the reaction proceeds, and H2 is oxidized to H+ at the platinum electrode. In this cell, the copper strip is the cathode, and the hydrogen electrode is the anode. The cell diagram therefore is written with the SHE on the left and the Cu2+/Cu couple on the right:
\[Pt_{(s)}∣H_2(g, 1 atm)∣H^+(aq, 1\; M)∥Cu^{2+}(aq, 1 M)∣Cu_{(s)} \label{20.4.8}\]
The half-cell reactions and potentials of the spontaneous reaction are as follows:
- Cathode: \[Cu^{2+}{(aq)} + 2e^− \rightarrow Cu_{(g)}\;\;\; E°_{cathode} = 0.34\; V \label{20.4.9}\]
- Anode: \[H_{2(g)} \rightarrow 2H^+_{(aq)} + 2e^−\;\;\; E°_{anode} = 0\; V \label{20.4.10}\]
- Overall: \[H_{2(g)} + Cu^{2+}_{(aq)} \rightarrow 2H^+_{(aq)} + Cu_{(s)} \label{20.4.11}\]
Thus the standard electrode potential for the Cu2+/Cu couple is 0.34 V.
Calculating Standard Cell Potentials
The standard cell potential for a redox reaction (E°cell) is a measure of the tendency of reactants in their standard states to form products in their standard states; consequently, it is a measure of the driving force for the reaction, which earlier we called voltage. We can use the two standard electrode potentials we found earlier to calculate the standard potential for the Zn/Cu cell represented by the following cell diagram:
\[ Zn{(s)}∣Zn^{2+}(aq, 1 M)∥Cu^{2+}(aq, 1 M)∣Cu_{(s)} \label{20.4.32}\]
We know the values of E°anode for the reduction of Zn2+ and E°cathode for the reduction of Cu2+, so we can calculate \(E°_{cell}\):
- cathode: \[Cu^{2+}_{(aq)} + 2e^− \rightarrow Cu_{(s)} \;\;\; E°_{cathode} = 0.34\; V \label{20.4.33}\]
- anode: \[Zn_{(s)} \rightarrow Zn^{2+}(aq, 1 M) + 2e^−\;\;\; E°_{anode} = −0.76\; V \label{20.4.34}\]
- overall: \[Zn_{(s)} + Cu^{2+}_{(aq)} \rightarrow Zn^{2+}_{(aq)} + Cu_{(s)} \label{20.4.35}\]
\[E°_{cell} = E°_{cathode} − E°_{anode} = 1.10\; V\]
This is the same value that is observed experimentally. If the value of \(E°_{cell}\) is positive, the reaction will occur spontaneously as written. If the value of \(E°_{cell}\) is negative, then the reaction is not spontaneous, and it will not occur as written under standard conditions; it will, however, proceed spontaneously in the opposite direction. As we shall see in Section 20.9, this does not mean that the reaction cannot be made to occur at all under standard conditions. With a sufficient input of electrical energy, virtually any reaction can be forced to occur. Example \(\PageIndex{2}\) and its corresponding exercise illustrate how we can use measured cell potentials to calculate standard potentials for redox couples.
A positive \(E°_{cell}\) means that the reaction will occur spontaneously as written. A negative \(E°_{cell}\) means that the reaction will proceed spontaneously in the opposite direction.
Example \(\PageIndex{1}\)
A galvanic cell with a measured standard cell potential of 0.27 V is constructed using two beakers connected by a salt bridge. One beaker contains a strip of gallium metal immersed in a 1 M solution of GaCl3, and the other contains a piece of nickel immersed in a 1 M solution of NiCl2. The half-reactions that occur when the compartments are connected are as follows:
cathode: Ni2+(aq) + 2e− → Ni(s)
anode: Ga(s) → Ga3+(aq) + 3e−
If the potential for the oxidation of Ga to Ga3+ is 0.55 V under standard conditions, what is the potential for the oxidation of Ni to Ni2+?
Given: galvanic cell, half-reactions, standard cell potential, and potential for the oxidation half-reaction under standard conditions
Asked for: standard electrode potential of reaction occurring at the cathode
Strategy:
- Write the equation for the half-reaction that occurs at the anode along with the value of the standard electrode potential for the half-reaction.
- Use Equation \(\ref{20.4.2}\) to calculate the standard electrode potential for the half-reaction that occurs at the cathode. Then reverse the sign to obtain the potential for the corresponding oxidation half-reaction under standard conditions.
Solution:
A We have been given the potential for the oxidation of Ga to Ga3+ under standard conditions, but to report the standard electrode potential, we must reverse the sign. For the reduction reaction Ga3+(aq) + 3e− → Ga(s), E°anode = −0.55 V.
B Using the value given for \(E°_{cell}\) and the calculated value of E°anode, we can calculate the standard potential for the reduction of Ni2+ to Ni from Equation \(\ref{20.4.2}\):
This is the standard electrode potential for the reaction Ni2+(aq) + 2e− → Ni(s). Because we are asked for the potential for the oxidation of Ni to Ni2+ under standard conditions, we must reverse the sign of E°cathode. Thus E° = −(−0.28 V) = 0.28 V for the oxidation. With three electrons consumed in the reduction and two produced in the oxidation, the overall reaction is not balanced. Recall, however, that standard potentials are independent of stoichiometry.
Exercise \(\PageIndex{1}\)
A galvanic cell is constructed with one compartment that contains a mercury electrode immersed in a 1 M aqueous solution of mercuric acetate \(Hg(CH_3CO_2)_2\) and one compartment that contains a strip of magnesium immersed in a 1 M aqueous solution of \(MgCl_2\). When the compartments are connected, a potential of 3.22 V is measured and the following half-reactions occur:
- cathode: Hg2+(aq) + 2e− → Hg(l)
- anode: Mg(s) → Mg2+(aq) + 2e−
If the potential for the oxidation of Mg to Mg2+ is 2.37 V under standard conditions, what is the standard electrode potential for the reaction that occurs at the anode?
- Answer
-
0.85 V
Summary
Redox reactions can be balanced using the half-reaction method. The standard cell potential is a measure of the driving force for the reaction. \(E°_{cell} = E°_{cathode} − E°_{anode} \) The flow of electrons in an electrochemical cell depends on the identity of the reacting substances, the difference in the potential energy of their valence electrons, and their concentrations. The potential of the cell under standard conditions (1 M for solutions, 1 atm for gases, pure solids or liquids for other substances) and at a fixed temperature (25°C) is called the standard cell potential (E°cell). Only the difference between the potentials of two electrodes can be measured. By convention, all tabulated values of standard electrode potentials are listed as standard reduction potentials. The overall cell potential is the reduction potential of the reductive half-reaction minus the reduction potential of the oxidative half-reaction (E°cell = E°cathode − E°anode). The potential of the standard hydrogen electrode (SHE) is defined as 0 V under standard conditions. The potential of a half-reaction measured against the SHE under standard conditions is called its standard electrode potential. The standard cell potential is a measure of the driving force for a given redox reaction. All E° values are independent of the stoichiometric coefficients for the half-reaction. Redox reactions can be balanced using the half-reaction method, in which the overall redox reaction is divided into an oxidation half-reaction and a reduction half-reaction, each balanced for mass and charge. The half-reactions selected from tabulated lists must exactly reflect reaction conditions. In an alternative method, the atoms in each half-reaction are balanced, and then the charges are balanced. Whenever a half-reaction is reversed, the sign of E° corresponding to that reaction must also be reversed. If \(E°_{cell}\) is positive, the reaction will occur spontaneously under standard conditions. If \(E°_{cell}\) is negative, then the reaction is not spontaneous under standard conditions, although it will proceed spontaneously in the opposite direction. The potential of an indicator electrode is related to the concentration of the substance being measured, whereas the potential of the reference electrode is held constant. Whether reduction or oxidation occurs depends on the potential of the sample versus the potential of the reference electrode. In addition to the SHE, other reference electrodes are the silver–silver chloride electrode; the saturated calomel electrode (SCE); the glass electrode, which is commonly used to measure pH; and ion-selective electrodes, which depend on the concentration of a single ionic species in solution. Differences in potential between the SHE and other reference electrodes must be included when calculating values for E°.

