8.9 Buffer Capacity and Buffer Range
- Page ID
- 163841
Buffer Capacity
Buffers are characterized by the pH range over which they can maintain a more or less constant pH and by their buffer capacity, the amount of strong acid or base that can be absorbed before the pH changes significantly. Although the useful pH range of a buffer depends strongly on the chemical properties of the weak acid and weak base used to prepare the buffer (i.e., on \(K\)), its buffer capacity depends solely on the concentrations of the species in the buffered solution. The more concentrated the buffer solution, the greater its buffer capacity. As illustrated in Figure \(\PageIndex{1}\), when \(NaOH\) is added to solutions that contain different concentrations of an acetic acid/sodium acetate buffer, the observed change in the pH of the buffer is inversely proportional to the concentration of the buffer. If the buffer capacity is 10 times larger, then the buffer solution can absorb 10 times more strong acid or base before undergoing a significant change in pH.
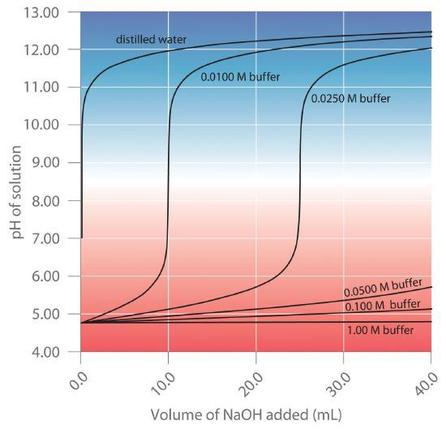
Figure \(\PageIndex{1}\): Effect of Buffer Concentration on the Capacity of a Buffer
A buffer maintains a relatively constant pH when acid or base is added to a solution. The addition of even tiny volumes of 0.10 M \(NaOH\) to 100.0 mL of distilled water results in a very large change in pH. As the concentration of a 50:50 mixture of sodium acetate/acetic acid buffer in the solution is increased from 0.010 M to 1.00 M, the change in the pH produced by the addition of the same volume of \(NaOH\) solution decreases steadily. For buffer concentrations of at least 0.500 M, the addition of even 25 mL of the \(NaOH\) solution results in only a relatively small change in pH.
Selecting proper components for desired pH
Buffers function best when the pKa of the conjugate weak acid used is close to the desired working range of the buffer. This turns out to be the case when the concentrations of the conjugate acid and conjugate base are approximately equal (within about a factor of 10). For example, we know the Ka for hydroflouric acid is 6.6 x 10-4 so its pKa= -log(6.6 x 10-4) = 3.18. So, a hydrofluoric acid buffer would work best in a buffer range of around pH = 3.18.
For the weak base ammonia (NH3), the value of Kb is 1.8x10-5, implying that the Ka for the dissociation of its conjugate acid, NH4+, is Kw/Kb=10-14/1.8x10-5 = 5.6x10-10. Thus, the pKa for NH4+ = 9.25, so buffers using NH4+/NH3 will work best around a pH of 9.25. (It's always the pKa of the conjugate acid that determines the approximate pH for a buffer system, though this is dependent on the pKb of the conjugate base, obviously.)
When the desired pH of a buffer solution is near the pKa of the conjugate acid being used (i.e., when the amounts of conjugate acid and conjugate base in solution are within about a factor of 10 of each other), the Henderson-Hasselbalch equation can be applied as a simple approximation of the solution pH, as we will see in the next section.
Example 1: HF Buffer
In this example we will continue to use the hydrofluoric acid buffer. We will discuss the process for preparing a buffer of HF at a pH of 3.0. We can use the Henderson-Hasselbalch approximation to calculate the necessary ratio of F- and HF.
\[pH = pKa + \log\dfrac{[Base]}{[Acid]}\]
\[3.0 = 3.18 + \log\dfrac{[Base]}{[Acid]}\]
\[\log\dfrac{[Base]}{[Acid]} = -0.18\]
\[\dfrac{[Base]}{[Acid]} = 10^{-0.18}\]
\[\dfrac{[Base]}{[Acid]} = 0.66\]
This is simply the ratio of the concentrations of conjugate base and conjugate acid we will need in our solution. However, what if we have 100 ml of 1 M HF and we want to prepare a buffer using NaF? How much Sodium Fluoride would we need to add in order to create a buffer at said pH (3.0)?
We know from our Henderson-Hasselbalch calculation that the ratio of our base/acid should be equal to 0.66. From a table of molar masses, such as a periodic table, we can calculate the molar mass of NaF to be equal to 41.99 g/mol. HF is a weak acid with a Ka = 6.6 x 10-4 and the concentration of HF is given above as 1 M. Using this information, we can calculate the amount of F- we need to add.
The dissociation reaction is:
\[HF_{(aq)} + H_2O_{(l)} \rightleftharpoons F^-_{(aq)} + H_3O^+_{(aq)}\]
We could use ICE tables to calculate the concentration of F- from HF dissociation, but, since Ka is so small, we can approximate that virtually all of the HF will remain undissociated, so the amount of F- in the solution from HF dissociation will be negligible. Thus, the [HF] is about 1 M and the [F-] is close to 0. This will be especially true once we have added more F-, the addition of which will even further suppress the dissociation of HF.
We want the ratio of Base/Acid to be 0.66, so we will need [Base]/1M = 0.66. Thus, [F-] should be about 0.66 M. For 100 mL of solution, then, we will want to add 0.066 moles (0.1 L x 0.66 M) of F-. Since we are adding NaF as our source of F-, and since NaF completely dissociates in water, we need 0.066 moles of NaF. Thus, 0.066 moles x 41.99 g/mol = 2.767 g.
Note that, since the conjugate acid and the conjugate base are both mixed into the same volume of solution in the buffer, the ratio of "Base/Acid" is the same whether we use a ratio of the "concentration of base over concentration of acid," OR a ratio of "moles of base over moles of acid." The pH of the solution does not, it turns out, depend on the volume! (This is only true so long as the solution does not get so dilute that the autoionization of water becomes an important source of H+ or OH-. Such dilute solutions are rarely used as buffers, however.)
References
- Brown, et al. Chemistry:The Central Science. 11th ed. Upper Saddle River, New Jersey: Pearson/Prentice Hall, 2008.
- Chang, Raymond. General Chemistry:The Essential Concepts. 3rd ed. New York: Mcgraw Hill, 2003
- Petrucci, et al. General Chemistry: Principles & Modern Applications. 9th ed. Upper Saddle River, New Jersey: Pearson/Prentice Hall, 2007.
Outside Links
Contributors
- Jose Pietri (UCD), Donald Land (UCD)

