7.8 Quantifying Heat
- Page ID
- 155868
Skills to Develop
- Distinguish the related properties of heat, thermal energy, and temperature
Thermal energy is kinetic energy associated with the random motion of atoms and molecules. Temperature is a quantitative measure of “hot” or “cold.” Temperature can also be thought of as a relative scale that allows us to determine the likely direction that heat will flow. When the atoms and molecules in an object are moving or vibrating quickly, they have a higher average kinetic energy (KE), and we say that the object is “hot.” When the atoms and molecules are moving slowly, they have lower KE, and we say that the object is “cold” (Figure \(\PageIndex{1}\)). Assuming that no chemical reaction or phase change (such as melting or vaporizing) occurs, increasing the amount of thermal energy in a sample of matter will cause its temperature to increase. And, assuming that no chemical reaction or phase change (such as condensation or freezing) occurs, decreasing the amount of thermal energy in a sample of matter will cause its temperature to decrease.
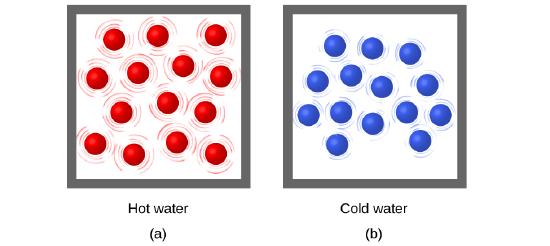
Figure \(\PageIndex{1}\): (a) The molecules in a sample of hot water move more rapidly than (b) those in a sample of cold water.
Heat (q) is the transfer of thermal energy between two bodies at different temperatures. Heat flow (a redundant term, but one commonly used) increases the thermal energy of one body and decreases the thermal energy of the other. Suppose we initially have a high temperature (and high thermal energy) substance (H) and a low temperature (and low thermal energy) substance (L). The atoms and molecules in H have a higher average KE than those in L. If we place substance H in contact with substance L, the thermal energy is very likely to flow from substance H to substance L. The temperature of substance H will decrease, as will the average KE of its molecules; the temperature of substance L will increase, along with the average KE of its molecules. Heat flow will continue until the two substances are at the same temperature (thermal equilibrium) (Figure \(\PageIndex{2}\)).
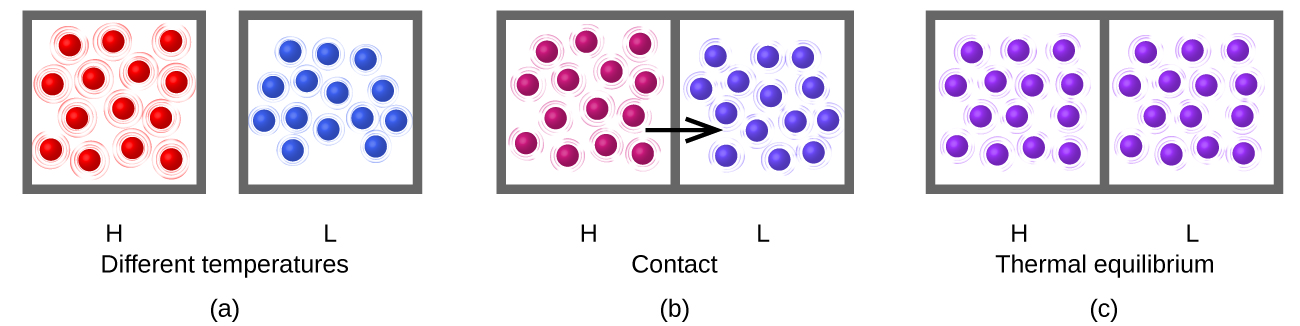
Figure \(\PageIndex{2}\): (a) Substances H and L are initially at different temperatures, and their atoms have different average kinetic energies. (b) When they are put into contact with each other, collisions between the molecules result in the transfer of kinetic (thermal) energy from the hotter to the cooler matter. (c) The two objects reach “thermal equilibrium” when both substances are at the same temperature, and their molecules have the same average kinetic energy.
Matter undergoing chemical reactions and physical changes can release or absorb heat. A change that releases heat is called an exothermic process. For example, the combustion reaction that occurs when using an oxyacetylene torch is an exothermic process—this process also releases energy in the form of light as evidenced by the torch’s flame (Figure \(\PageIndex{3a}\)). A reaction or change that absorbs heat is an endothermic process. A cold pack used to treat muscle strains provides an example of an endothermic process. When the substances in the cold pack (water and a salt like ammonium nitrate) are brought together, the resulting process absorbs heat, leading to the sensation of cold.

Figure \(\PageIndex{3}\): (a) An oxyacetylene torch produces heat by the combustion of acetylene in oxygen. The energy released by this exothermic reaction heats and then melts the metal being cut. The sparks are tiny bits of the molten metal flying away. (b) A cold pack uses an endothermic process to create the sensation of cold. (credit a: modification of work by “Skatebiker”/Wikimedia commons).
Historically, energy was measured in units of calories (cal). A calorie is the amount of energy required to raise one gram of water by 1 degree C (also 1 kelvin). However, this quantity depends on the atmospheric pressure and the starting temperature of the water. The ease of measurement of energy changes in calories has meant that the calorie is still frequently used. The Calorie (with a capital C), or large calorie, commonly used in quantifying food energy content, is a kilocalorie. The SI unit of heat, work, and energy is the joule. A joule (J) is defined as the amount of energy used when a force of 1 newton moves an object 1 meter. It is named in honor of the English physicist James Prescott Joule. One joule is equivalent to 1 kg m2/s2, which is also called 1 newton–meter. A kilojoule (kJ) is 1000 joules. To standardize its definition, 1 calorie has been set to equal 4.184 joules.
\[1\,cal \equiv 4.184\, J\]
Application: Heat can do more than increase temperature
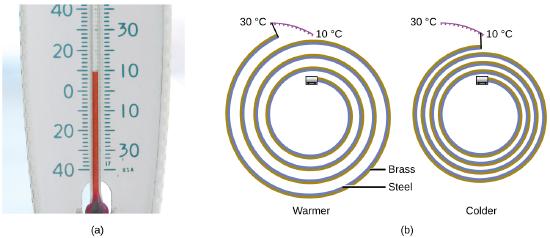
Most substances expand as their temperature increases and contract as their temperature decreases. This property can be used to measure temperature changes, as shown in Figure \(\PageIndex{4}\). The operation of many thermometers depends on the expansion and contraction of substances in response to temperature changes.
Figure \(\PageIndex{4}\): (a) In an alcohol or mercury thermometer, the liquid (dyed red for visibility) expands when heated and contracts when cooled, much more so than the glass tube that contains the liquid. (b) In a bimetallic thermometer, two different metals (such as brass and steel) form a two-layered strip. When heated or cooled, one of the metals (brass) expands or contracts more than the other metal (steel), causing the strip to coil or uncoil. Both types of thermometers have a calibrated scale that indicates the temperature. (credit a: modification of work by “dwstucke”/Flickr). (c) The demonstration allows one to view the effects of heating and cooling a coiled bimetallic strip.A bimetallic coil from a thermometer reacts to the heat from a lighter, by uncoiling and then coiling back up when the lighter is removed. Animation used with permission from Hustvedt (via Wikipedia)
Direction of Heat Flow: Endothermic vs. Exothermic Processes
The reaction of powdered aluminum with iron(III) oxide, known as the thermite reaction, generates an enormous amount of heat—enough, in fact, to melt steel. The balanced chemical equation for the reaction is as follows:
\[ \ce{2Al(s) + Fe_2O_3(s) \rightarrow 2Fe(s) + Al_2O_3(s) }\label{12.2.1}\]
We can also write this chemical equation as
\[\ce{2Al(s) + Fe_2O_3(s) \rightarrow 2Fe(s) + Al_2O_3(s)} + \text{heat} \label{12.2.2}\]
to indicate that heat is one of the products. Chemical equations in which heat is shown as either a reactant or a product are called thermochemical equations. In this reaction, the system consists of aluminum, iron, and oxygen atoms; everything else, including the container, makes up the surroundings. During the reaction, so much heat is produced that the iron liquefies. Eventually, the system cools; the iron solidifies as heat is transferred to the surroundings. A process in which heat (\(q\)) is transferred from a system to its surroundings is described as exothermic. By convention, \(q < 0\) for an exothermic reaction.
When you hold an ice cube in your hand, heat from the surroundings (including your hand) is transferred to the system (the ice), causing the ice to melt and your hand to become cold. We can describe this process by the following thermochemical equation:
\[ \text{heat} + \ce{H_2O_{(s)} \rightarrow H_2O_{(l)}} \label{12.2.3}\]
When heat is transferred to a system from its surroundings, the process is endothermic. By convention, \(q > 0\) for an endothermic reaction.
By convention, \(q < 0\) for an exothermic reaction and \(q > 0\) for an endothermic reaction.
Exercise \(\PageIndex{1}\)
Decide whether the following are endothermic or exothermic processes
- water evaporates off a shower door
- an acid tablet being added to a pool and the surrounding water heats up
- \(\ce{NH_4Cl}\) is dissolved in water and the solution cools
- the burning of a log in a campfire
- Hint
-
During an endothermic process heat is absorbed from surroundings, causing them to cool, so in every case where there is cooling there is most likely an endothermic process taking place. For exothermic reactions energy is being released to the surroundings and so the surroundings feel like they have been heated by the process.
- Answer a
-
endothermic
- Answer b
-
exothermic
- Answer c
-
endothermic
- Answer d
-
exothermic
Heat is technically not a component in Chemical Reactions
Technically, it is poor form to have a \(heat\) term in the chemical reaction like in Equations \(\ref{12.2.2}\) and \(\ref{12.2.3}\) since is it not a true species in the reaction. However, this is a convenient approach to represent exothermic and endothermic behavior and is commonly used by chemists.
Measuring Heat
Because ΔH is defined as the gain or loss of heat at constant pressure, measurements made using a constant-pressure calorimeter (a device used to measure enthalpy changes in processes at constant pressure) give ΔH values directly. This device is particularly well suited to studying reactions carried out in solution at a constant atmospheric pressure. A “student” version, called a coffee-cup calorimeter (Figure \(\PageIndex{5}\)), is often encountered in general chemistry laboratories. Commercial calorimeters operate on the same principle, but they can be used with smaller volumes of solution, have better thermal insulation, and can detect a change in temperature as small as several millionths of a degree (10−6 °C). Because the heat released or absorbed at constant pressure is equal to ΔH, the relationship between heat and \(ΔH_{rxn}\) is
\[ \Delta H_{rxn}=q_{system}=-q_{calorimeter}=-mC \Delta T \label{7.3.1} \]
The use of a constant-pressure calorimeter is illustrated in Example \(\PageIndex{1}\).
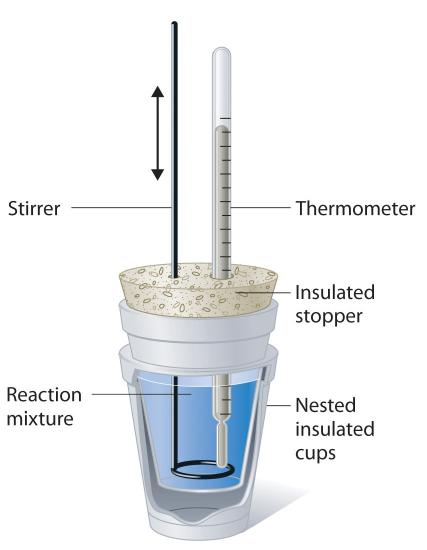
Figure \(\PageIndex{5}\): A Coffee-Cup Calorimeter. This simplified version of a constant-pressure calorimeter consists of two Styrofoam cups nested and sealed with an insulated stopper to thermally isolate the system (the solution being studied) from the surroundings (the air and the laboratory bench). Two holes in the stopper allow the use of a thermometer to measure the temperature and a stirrer to mix the reactants.
Example \(\PageIndex{1}\)
If 2500. Joules of heat are transferred to a 25.5 gram solid with a specific heat capacity of \(1.437 \dfrac{J}{g·^oC} \), by how many degrees Celsius will the temperature of the solid increase?
Given: mass of a solid, specific heat of solid, heat added.
Asked for: Temperature increase of solid, \( \Delta T\)
Strategy:
Calculate change in temperature of water using Equation 7.3.1
Solution:
\( \Delta T = \dfrac{q}{mass \times C} = \dfrac{2500. J}{(25.5 g) \left( 1.437 \dfrac{J}{g·^oC} \right) } = 68.2^oC \)
Exercise \(\PageIndex{2}\)
If 1507. Joules of heat are transferred to a 26.50 gram solid, and the temperature of the solid increases by 27.85oC, what is the specific heat capacity of the solid, in \( \dfrac{J}{g·^oC} \)?
- Answer
-
\(2.042 \dfrac{J}{g·^oC} \)
Example \(\PageIndex{2}\):
A 25.7 gram piece of solid is heated to 98.7 oC and then placed in 150.2 grams of water in a calorimeter at 20.2oC. After sitting for several minutes, the temperature of the water stabilizes at 22.3oC. The specific heat of water is 4.184 \(\dfrac{J}{g·^oC}\). Calculate the specific heat of the piece of solid.
Given: mass of a solid, mass of water, specific heat of water, initial and final temperatures.
Asked for: C of solid
Strategy:
A. Calculate change in heat of water using Equation 7.3.1
B. Calculate C of solid, given that qwater = -qsolid
Solution:
A. qwater = \(150.2 g \times 4.184 \dfrac{J}{g·^oC} \times (22.3^oC - 20.2^oC) = 1320 J \)
B. qsolid = -qwater = \(-1320 J = 25.7 g \times C_{solid} \times (22.3^oC - 98.7^oC)\)
\(C_{solid} = \dfrac{-1320 J}{(25.7 g)(-76.4^oC)} = 0.672 \dfrac{J}{g·^oC} \)
Exercise \(\PageIndex{3}\)
A 14.8 gram piece of solid is heated to 100.2 oC and then placed in 102 grams of water in a calorimeter at 21.3oC. After sitting for several minutes, the temperature of the water stabilizes at 22.9oC. The specific heat of water is 4.184 \(\dfrac{J}{g·^oC}\). Calculate the specific heat of the piece of solid.
- Answer
-
0.597 \( \dfrac{J}{g·^oC} \)
Heating and Cooling Curves for Water
Freezing, condensation, and deposition, which are the reverse of fusion, sublimation, and vaporization—are exothermic. Thus heat pumps that use refrigerants are essentially air-conditioners running in reverse. Heat from the environment is used to vaporize the refrigerant, which is then condensed to a liquid in coils within a house to provide heat. The energy changes that occur during phase changes can be quantified by using a heating or cooling curve.
Heating Curves
Figure \(\PageIndex{6}\) shows a heating curve, a plot of temperature versus heating time, for a 75 g sample of water. The sample is initially ice at 1 atm and −23°C; as heat is added, the temperature of the ice increases linearly with time. The slope of the line depends on both the mass of the ice and the specific heat (Cs) of ice, which is the number of joules required to raise the temperature of 1 g of ice by 1°C. As the temperature of the ice increases, the water molecules in the ice crystal absorb more and more energy and vibrate more vigorously. At the melting point, they have enough kinetic energy to overcome attractive forces and move with respect to one another. As more heat is added, the temperature of the system does not increase further but remains constant at 0°C until all the ice has melted. Once all the ice has been converted to liquid water, the temperature of the water again begins to increase. Now, however, the temperature increases more slowly than before because the specific heat capacity of water is greater than that of ice. When the temperature of the water reaches 100°C, the water begins to boil. Here, too, the temperature remains constant at 100°C until all the water has been converted to steam. At this point, the temperature again begins to rise, but at a faster rate than seen in the other phases because the heat capacity of steam is less than that of ice or water.
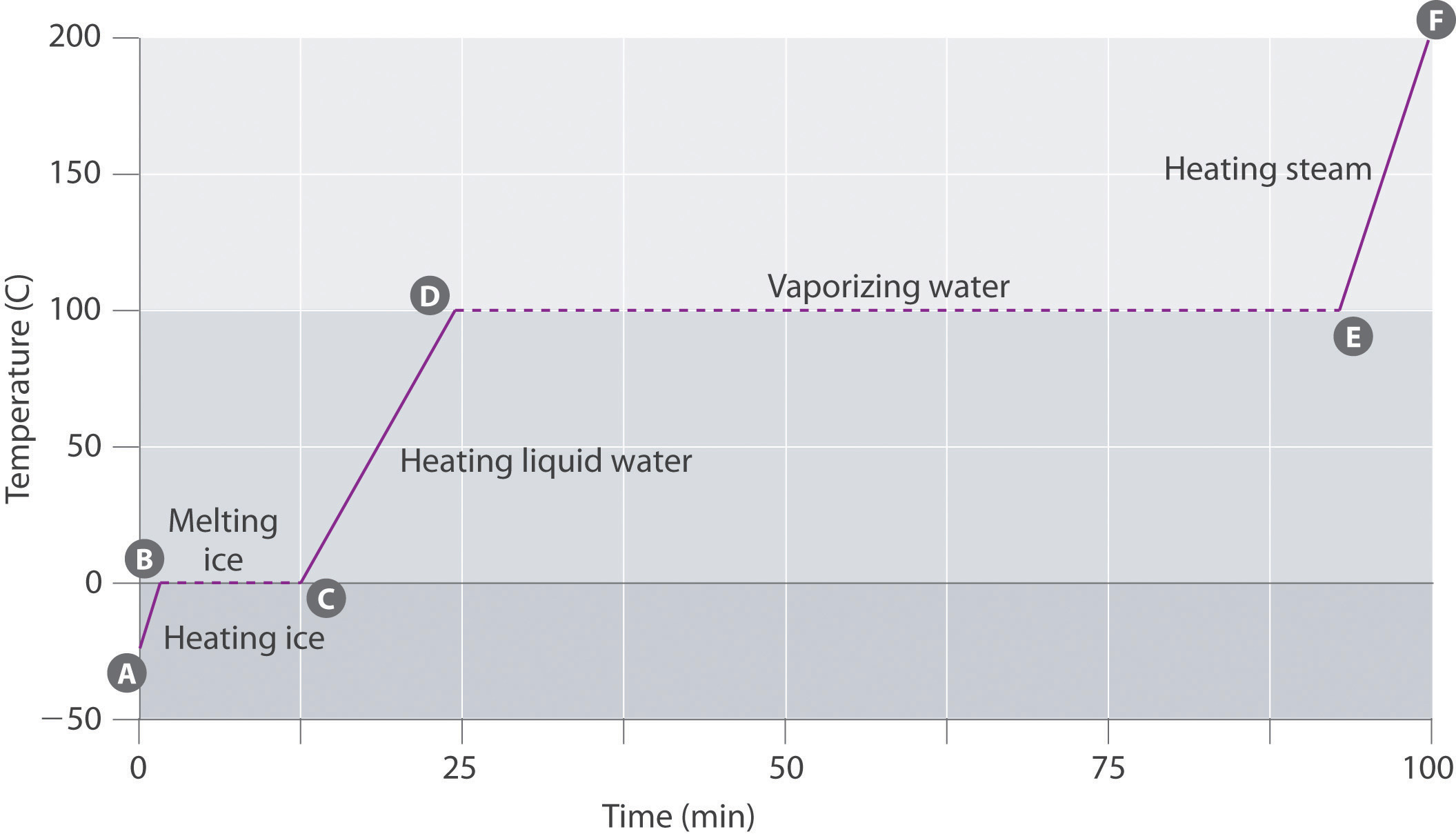
Figure \(\PageIndex{6}\): A Heating Curve for Water. This plot of temperature shows what happens to a 75 g sample of ice initially at 1 atm and −23°C as heat is added at a constant rate: A–B: heating solid ice; B–C: melting ice; C–D: heating liquid water; D–E: vaporizing water; E–F: heating steam.
Thus the temperature of a system does not change during a phase change. In this example, as long as even a tiny amount of ice is present, the temperature of the system remains at 0°C during the melting process, and as long as even a small amount of liquid water is present, the temperature of the system remains at 100°C during the boiling process. The rate at which heat is added does not affect the temperature of the ice/water or water/steam mixture because the added heat is being used exclusively to overcome the attractive forces that hold the more condensed phase together. Many cooks think that food will cook faster if the heat is turned up higher so that the water boils more rapidly. Instead, the pot of water will boil to dryness sooner, but the temperature of the water does not depend on how vigorously it boils.
The temperature of a sample does not change during a phase change.
If heat is added at a constant rate, as in Figure \(\PageIndex{6}\), then the length of the horizontal lines, which represents the time during which the temperature does not change, is directly proportional to the magnitude of the enthalpies associated with the phase changes. In Figure \(\PageIndex{6}\), the horizontal line at 100°C is much longer than the line at 0°C because the enthalpy of vaporization of water is several times greater than the enthalpy of fusion.
A superheated liquid is a sample of a liquid at the temperature and pressure at which it should be a gas. Superheated liquids are not stable; the liquid will eventually boil, sometimes violently. The phenomenon of superheating causes “bumping” when a liquid is heated in the laboratory. When a test tube containing water is heated over a Bunsen burner, for example, one portion of the liquid can easily become too hot. When the superheated liquid converts to a gas, it can push or “bump” the rest of the liquid out of the test tube. Placing a stirring rod or a small piece of ceramic (a “boiling chip”) in the test tube allows bubbles of vapor to form on the surface of the object so the liquid boils instead of becoming superheated. Superheating is the reason a liquid heated in a smooth cup in a microwave oven may not boil until the cup is moved, when the motion of the cup allows bubbles to form.
Cooling Curves
The cooling curve, a plot of temperature versus cooling time, in Figure \(\PageIndex{7}\) plots temperature versus time as a 75 g sample of steam, initially at 1 atm and 200°C, is cooled. Although we might expect the cooling curve to be the mirror image of the heating curve in Figure \(\PageIndex{6}\), the cooling curve is not an identical mirror image. As heat is removed from the steam, the temperature falls until it reaches 100°C. At this temperature, the steam begins to condense to liquid water. No further temperature change occurs until all the steam is converted to the liquid; then the temperature again decreases as the water is cooled. We might expect to reach another plateau at 0°C, where the water is converted to ice; in reality, however, this does not always occur. Instead, the temperature often drops below the freezing point for some time, as shown by the little dip in the cooling curve below 0°C. This region corresponds to an unstable form of the liquid, a supercooled liquid. If the liquid is allowed to stand, if cooling is continued, or if a small crystal of the solid phase is added (a seed crystal), the supercooled liquid will convert to a solid, sometimes quite suddenly. As the water freezes, the temperature increases slightly due to the heat evolved during the freezing process and then holds constant at the melting point as the rest of the water freezes. Subsequently, the temperature of the ice decreases again as more heat is removed from the system.
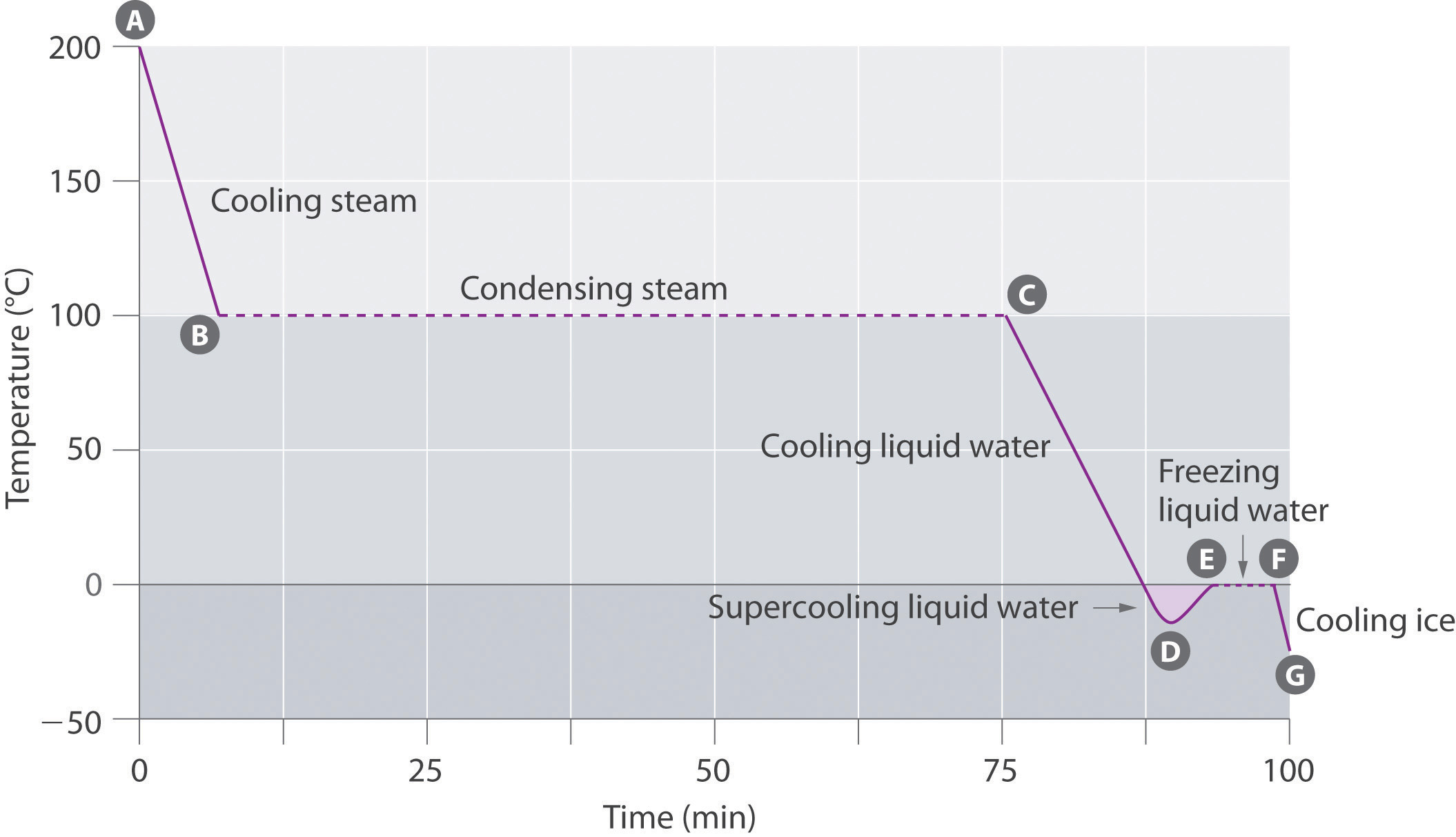
Figure \(\PageIndex{7}\): A Cooling Curve for Water. This plot of temperature shows what happens to a 75 g sample of steam initially at 1 atm and 200°C as heat is removed at a constant rate: A–B: cooling steam; B–C: condensing steam; C–D: cooling liquid water to give a supercooled liquid; D–E: warming the liquid as it begins to freeze; E–F: freezing liquid water; F–G: cooling ice.
Supercooling effects have a huge impact on Earth’s climate. For example, supercooling of water droplets in clouds can prevent the clouds from releasing precipitation over regions that are persistently arid as a result. Clouds consist of tiny droplets of water, which in principle should be dense enough to fall as rain. In fact, however, the droplets must aggregate to reach a certain size before they can fall to the ground. Usually a small particle (a nucleus) is required for the droplets to aggregate; the nucleus can be a dust particle, an ice crystal, or a particle of silver iodide dispersed in a cloud during seeding (a method of inducing rain). Unfortunately, the small droplets of water generally remain as a supercooled liquid down to about −10°C, rather than freezing into ice crystals that are more suitable nuclei for raindrop formation. One approach to producing rainfall from an existing cloud is to cool the water droplets so that they crystallize to provide nuclei around which raindrops can grow. This is best done by dispersing small granules of solid CO2 (dry ice) into the cloud from an airplane. Solid CO2 sublimes directly to the gas at pressures of 1 atm or lower, and the enthalpy of sublimation is substantial (25.3 kJ/mol). As the CO2 sublimes, it absorbs heat from the cloud, often with the desired results.
Example \(\PageIndex{3}\): Cooling Hot Tea
If a 50.0 g ice cube at 0.0°C is added to 500 mL of tea at 20.0°C, what is the temperature of the tea when the ice cube has just melted? Assume that no heat is transferred to or from the surroundings. The density of water (and iced tea) is 1.00 g/mL over the range 0°C–20°C, the specific heats of liquid water and ice are 4.184 J/(g•°C) and 2.062 J/(g•°C), respectively, and the enthalpy of fusion of ice is 6.01 kJ/mol.
Given: mass, volume, initial temperature, density, specific heats, and \(ΔH_{fus}\)
Asked for: final temperature
Strategy:
Substitute the values given into the general equation relating heat gained to heat lost (Equation 5.39) to obtain the final temperature of the mixture.
Solution:
When two substances or objects at different temperatures are brought into contact, heat will flow from the warmer one to the cooler. The amount of heat that flows is given by
\[q=mC_sΔT\]
where q is heat, m is mass, Cs is the specific heat, and ΔT is the temperature change. Eventually, the temperatures of the two substances will become equal at a value somewhere between their initial temperatures. Calculating the temperature of iced tea after adding an ice cube is slightly more complicated. The general equation relating heat gained and heat lost is still valid, but in this case we also have to take into account the amount of heat required to melt the ice cube from ice at 0.0°C to liquid water at 0.0°C.
Exercise \(\PageIndex{4}\): Death by Freezing
Suppose you are overtaken by a blizzard while ski touring and you take refuge in a tent. You are thirsty, but you forgot to bring liquid water. You have a choice of eating a few handfuls of snow (say 400 g) at −5.0°C immediately to quench your thirst or setting up your propane stove, melting the snow, and heating the water to body temperature before drinking it. You recall that the survival guide you leafed through at the hotel said something about not eating snow, but you cannot remember why—after all, it’s just frozen water. To understand the guide’s recommendation, calculate the amount of heat that your body will have to supply to bring 400 g of snow at −5.0°C to your body’s internal temperature of 37°C. Use the data in Example \(\PageIndex{3}\)
Answer
200 kJ (4.1 kJ to bring the ice from −5.0°C to 0.0°C, 133.6 kJ to melt the ice at 0.0°C, and 61.9 kJ to bring the water from 0.0°C to 37°C), which is energy that would not have been expended had you first melted the snow.
Contributors
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).
- Modified by Tom Neils (Grand Rapids Community College)