7.5 Le Châtelier’s Principle: How a System at Equilibrium Responds to Disturbances
- Page ID
- 142274
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Skills to Develop
- Describe the ways in which an equilibrium system can be stressed
- Predict the response of a stressed equilibrium using Le Chatelier’s principle
As we saw in the previous section, reactions proceed in both directions (reactants go to products and products go to reactants). We can tell a reaction is at equilibrium if the reaction quotient (Q) is equal to the equilibrium constant (K). We next address what happens when a system at equilibrium is disturbed so that Q is no longer equal to K. If a system at equilibrium is subjected to a perturbance or stress (a change in concentration of one of the species in the law of mass action) the position of equilibrium changes. Since this stress affects the concentrations of the reactants and the products, the value of Q will no longer equal the value of K. To re-establish equilibrium, the system will either shift toward the products (if K > Q) or the reactants (if K < Q) until Q returns to the same value as K. This process is described by Le Chatelier's principle.
Le Chatelier's principle
When a chemical system at equilibrium is disturbed, it returns to equilibrium by counteracting the disturbance. As described in the previous paragraph, the disturbance causes a change in the value of Q; the reaction will shift to re-establish K = Q
Predicting the Direction of a Reversible Reaction
Le Chatelier's principle can be used to predict changes in equilibrium concentrations when a system that is at equilibrium is subjected to a stress. However, if we have a mixture of reactants and products that have not yet reached equilibrium, the changes necessary to reach equilibrium may not be so obvious. In such a case, we can compare the values of Q and K for the system to predict the changes.
A chemical system at equilibrium can be temporarily shifted out of equilibrium by adding or removing one or more of the reactants or products. The concentrations of both reactants and products then undergo additional changes to return the system to equilibrium.
The stress on the system in Figure 7.9.1 is the reduction of the equilibrium concentration of SCN− (lowering the concentration of one of the reactants would cause K to be larger than Q). As a consequence, Le Chatelier's principle leads us to predict that the concentration of Fe(SCN)2+ should decrease, increasing the concentration of SCN− part way back to its original concentration, and increasing the concentration of Fe3+ above its initial equilibrium concentration.
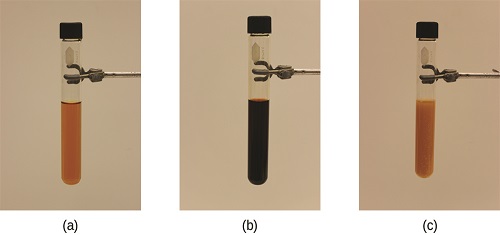
Figure 7.9.1: (a) The test tube contains 0.1 M Fe3+. (b) Thiocyanate ion has been added to solution in (a), forming the red Fe(SCN)2+ ion: \( Fe^{2+}_{(aq)} + SCN^-_{(aq)} \rightleftharpoons Fe(SCN)^{2+}_{(aq)} \) (c) Silver nitrate has been added to the solution in (b), precipitating some of the SCN− as the white solid AgSCN: \(Ag^+_{(aq)} + SCN^-_{(aq)} \rightleftharpoons AgSCN_{(s)} \). The decrease in the SCN− concentration shifts the first equilibrium in the solution to the left, decreasing the concentration of the Fe(SCN)2+, and lightening color. (credit: modification of work by Mark Ott).
The effect of a change in concentration on a system at equilibrium is illustrated further by the equilibrium of this chemical reaction:
\(H_{2(g)} + I_{2(g)} \rightleftharpoons 2HI_{g} \)
K = 50.0 at 400oC
- [H2] = 0.374 M
- [I2] = 0.153 M
- [HI] = 1.692 M
This gives
\(Q= \dfrac {[HI]^2}{[H_2][I_2]} \)
\(Q= \dfrac {[1.692]^2}{[0.374][0.153]} \)
\(Q = 50.0 = K \)
Even though we have stressed this system by introducing additional H2, the stress is relieved as the reaction shifts to the right, using up some (but not all) of the excess H2, reducing the amount of unreacted I2, and forming additional HI. There are new concentrations of all three substances, but the ratio of these concentrations, as described by the law of mass action, is once again equal to 50.0, because that is the fixed value of K for this reaction at this temperature.
Effect of Change in Pressure on Equilibrium
Sometimes we can change the position of equilibrium by changing the pressure of a system. However, changes in pressure have a measurable effect only in systems in which gases are involved, and then only when the chemical reaction produces a change in the total number of gas molecules in the system. In addition, the change in pressure must cause a change in concentration of the substances involved in the reaction. The only practical way to cause a concentration change by making a pressure change is to change the size of the container holding the gases. Some changes to total pressure, such as adding an inert gas that is not part of the equilibrium, will change the total pressure but not the partial pressures of the gases in the equilibrium constant expression. Thus, addition of a gas not involved in the equilibrium will not perturb the equilibrium.
As we increase the pressure of a gaseous system at equilibrium, either by decreasing the volume of the system or by adding more of one of the components of the equilibrium mixture, we introduce a stress by increasing the partial pressures of one or more of the components. In accordance with Le Chatelier's principle, a shift in the equilibrium that reduces the total number of molecules per unit of volume will be favored because this relieves the stress. The reverse reaction would be favored by a decrease in pressure.
Consider what happens if we shrink the flask, thus increasing the pressure on a system in which NO, O2, and NO2 are at equilibrium:
\(2NO_{(g)} + O_{2(g)} \rightleftharpoons NO_{2(g)} \)
Increasing the pressure causes the concentration of all of the gases to increase (because molarity is moles per Liter, and you just decreased the volume). To reattain equilibrium, the reaction will shift to the right, the side with fewer moles of gas. This shift to the right happens because it decreases the total number of molecules in the system because each time two molecules of NO2 form, a total of three molecules of NO and O2 are consumed. Thus, the shift to the right reduces the total pressure exerted by the system and leads to new concentrations of all of the gases that, when plugged into the law of mass action, result in K = Q.
On the other hand, expanding the flask will cause a decrease in the pressure on the system, which means that the concentrations of all the gases decrease. To reattain equilibrium, the reaction will shift to the left, the side with more moles of gas. This shift to the left happens because it increases the total number of molecules in the system because each time two molecules of NO2 are consumed, a total of three molecules of NO and O2 are formed. Thus, the shift to the left increases the total pressure exerted by the system and and leads to new concentrations of all of the gases that, when plugged into the law of mass action, result in K = Q.
Now consider this reaction:
\(N_{2(g)} + O_{2(g)} \rightleftharpoons 2NO_{(g)} \)
Because there is no change in the total number of molecules in the system during reaction, a change in pressure does not cause a shift away from equilibrium, because the value of Q will equal K throughout any pressure change.
Effect of Change in Temperature on Equilibrium
Changing concentration perturbs an equilibrium because the reaction quotient is shifted away from the equilibrium value. In other words, Q will not equal K at the instant of the change. Changing the temperature of a system at equilibrium has a different effect: A change in temperature actually changes the value of the equilibrium constant. However, we can qualitatively predict the effect of the temperature change by treating it as a stress on the system and applying Le Chatelier's principle.
When hydrogen reacts with gaseous iodine, heat is evolved.
\(H_{2(g)} + I_{2(g)} \rightleftharpoons 2HI_{(g)} \; \Delta H^o = -9.4 \; kJ \)
Because this reaction is exothermic, we can write it with heat as a product:
\(H_{2(g)} + I_{2(g)} \rightleftharpoons 2HI_{(g)} + heat \)
Increasing the temperature of the reaction increases the internal energy of the system. Thus, increasing the temperature has the effect of increasing the amount of heat, one of the products of this reaction. The reaction shifts to the left to relieve the stress, and there is an increase in the concentration of H2 and I2 and a reduction in the concentration of HI. Lowering the temperature of this system reduces the amount of energy present, favors the production of heat, and favors the formation of hydrogen iodide.
When we change the temperature of a system at equilibrium, the equilibrium constant for the reaction changes. Lowering the temperature in the HI system increases the equilibrium constant: At the new equilibrium the concentration of HI has increased and the concentrations of H2 and I2 decreased. Raising the temperature decreases the value of the equilibrium constant, from 67.5 at 357 °C to 50.0 at 400 °C.
Temperature affects the equilibrium between NO2 and N2O4 in the reaction:
\(N_2O_{4(g)} \rightleftharpoons 2NO_{2(g)} \; \Delta H^o = 57.2 \; kJ \)
The positive ΔH value tells us that the reaction is endothermic and could be written:
\( heat + N_2O_{4(g)} \rightleftharpoons 2NO_{2(g)} \)
At higher temperatures, the gas mixture has a deep brown color, indicative of a significant amount of brown NO2 molecules. If, however, we put a stress on the system by cooling the mixture (withdrawing energy), the equilibrium shifts to the left to supply some of the energy lost by cooling. The concentration of colorless N2O4 increases, and the concentration of brown NO2 decreases, causing the brown color to fade.
The overview of how different disturbances affect the reaction equilibrium properties is tabulated in Table 7.9.1
| Disturbance | Observed Change as Equilibrium is Restored | Direction of Shift | Effect on K |
|---|---|---|---|
| reactant added | added reactant is partially consumed | toward products | none |
| product added | added product is partially consumed | toward reactants | none |
| decrease in volume/increase in gas pressure | pressure decreases | toward side with fewer moles of gas | none |
| increase in volume/decrease in gas pressure | pressure increases | toward side with fewer moles of gas | none |
| temperature increase | heat is absorbed | toward products for endothermic, toward reactants for exothermic | changes |
| temperature decrease | heat is given off | toward reactants for endothermic, toward products for exothermic | changes |
Example \(\PageIndex{1}\)
Write an equilibrium constant expression for each reaction and use this expression to predict in which direction the reaction will shift to reattain equilibrium.
- \( 2 HgO_{(s)} \rightleftharpoons 2Hg_{(l)} +O_{2(g)} \): the amount of HgO is doubled.
- \(NH_4HS_{(s)} \rightleftharpoons NH_{3(g)} + H_2S_{(g)} \): the concentration of H2S is tripled
- \(n-butane_{(g)} \rightleftharpoons isobutane_{(g)} \): the concentration of isobutane is halved.
Given: equilibrium systems and changes
Asked for: equilibrium constant expressions and effects of changes
Strategy:
Write the equilibrium constant expression, remembering that pure liquids and solids do not appear in the expression. From this expression, predict the change that must occur to maintain equilibrium when the indicated changes are made.
Solution:
a. Because HgO is a pure solid and Hg is a pure liquid, they both are assigned an activity of '1' and their amounts do not appear in the equilibrium constant expression. Thus, for this reaction, K = [O2]. The equilibrium concentration of O2 is a constant and does not depend on the amount of HgO present. Hence adding more HgO will not affect the equilibrium concentration of O2 so no compensatory change is necessary. The reaction does not shift from equilibrium.
b. NH4HS is assign a value of '1' in the equilibrium constant expression because it is a solid. Thus K = [NH3][H2S], which means that the concentrations of the products are inversely proportional. If the concentration of H2S triples, for example, then the concentration of NH3 must decrease by about a factor of 3 for the system to remain at equilibrium so that the product of the concentrations (Q) equals K. The reaction must shift left to reach equilibrium.
c. For this reaction K = \(\dfrac{[isobutane]}{[n-butane]} \), so halving the concentration of isobutane means that the n-butane concentration must also decrease by about half if the system is to maintain equilibrium. The reaction must shift to the right to reach equilibrium.
Exercise \(\PageIndex{1}\)
In which direction will the reaction shift if the stated stress is placed on the reaction at equilibrium?
- \( HBr_{(g)} + NaH_{(s)} \rightleftharpoons NaBr_{(s)} +H_{2(g)} \): the concentration of HBr is decreased by a factor of 3.
- \(6 Li_{(s)} + N_{2(g)} \rightleftharpoons 2Li_3N_{(s)} \): the amount of Li is tripled.
- \(SO_{2(g)} + Cl_{2(g)} \rightleftharpoons SO_2Cl_{2(l)} \): the concentration of Cl2 is doubled.
- Answer
-
a. The reaction will shift left to reattain equilibrium because you removed reactant.
b. The reaction will not shift because Li is a solid
c. The reaction will shift to the right because you added a reactant.
Catalysts Do Not Affect Equilibrium
As we learned during our study of kinetics, a catalyst can speed up the rate of a reaction. Though this increase in reaction rate may cause a system to reach equilibrium more quickly (by speeding up the forward and reverse reactions), a catalyst has no effect on the value of an equilibrium constant nor on equilibrium concentrations. The interplay of changes in concentration or pressure, temperature, and the lack of an influence of a catalyst on a chemical equilibrium is illustrated in the industrial synthesis of ammonia from nitrogen and hydrogen according to the equation:
\( N_{2(g)} + 3 H_{2(g)} \rightleftharpoons 2 NH_{3(g)} \)
A large quantity of ammonia is manufactured by this reaction. Each year, ammonia is among the top 10 chemicals, by mass, manufactured in the world. About 2 billion pounds are manufactured in the United States each year. Ammonia plays a vital role in our global economy. It is used in the production of fertilizers and is, itself, an important fertilizer for the growth of corn, cotton, and other crops. Large quantities of ammonia are converted to nitric acid, which plays an important role in the production of fertilizers, explosives, plastics, dyes, and fibers, and is also used in the steel industry.
Fritz Haber
Haber was born in Breslau, Prussia (presently Wroclaw, Poland) in December 1868. He went on to study chemistry and, while at the University of Karlsruhe, he developed what would later be known as the Haber process: the catalytic formation of ammonia from hydrogen and atmospheric nitrogen under high temperatures and pressures. For this work, Haber was awarded the 1918 Nobel Prize in Chemistry for synthesis of ammonia from its elements as shown above. The Haber process was a boon to agriculture, as it allowed the production of fertilizers to no longer be dependent on mined feed stocks such as sodium nitrate.

Figure 7.9.2: The work of Nobel Prize recipient Fritz Haber revolutionized agricultural practices in the early 20th century. His work also affected wartime strategies, adding chemical weapons to the artillery.
Currently, the annual production of synthetic nitrogen fertilizers exceeds 100 million tons and synthetic fertilizer production has increased the number of humans that arable land can support from 1.9 persons per hectare in 1908 to 4.3 in 2008. The availability of nitrogen is a strong limiting factor to the growth of plants. Despite accounting for 78% of air, diatomic nitrogen (N2) is nutritionally unavailable to a majority of plants due the tremendous stability of the nitrogen-nitrogen triple bond. Therefore, the nitrogen must be converted to a more bioavailable form (this conversion is called nitrogen fixation). Legumes achieve this conversion at ambient temperature by exploiting bacteria equipped with suitable enzymes.
In addition to his work in ammonia production, Haber is also remembered by history as one of the fathers of chemical warfare. During World War I, he played a major role in the development of poisonous gases used for trench warfare. Regarding his role in these developments, Haber said, “During peace time a scientist belongs to the World, but during war time he belongs to his country.”1 Haber defended the use of gas warfare against accusations that it was inhumane, saying that death was death, by whatever means it was inflicted. He stands as an example of the ethical dilemmas that face scientists in times of war and the double-edged nature of the sword of science.
Like Haber, the products made from ammonia can be multifaceted. In addition to their value for agriculture, nitrogen compounds can also be used to achieve destructive ends. Ammonium nitrate has also been used in explosives, including improvised explosive devices. Ammonium nitrate was one of the components of the bomb used in the attack on the Alfred P. Murrah Federal Building in downtown Oklahoma City on April 19, 1995.
Summary
Systems at equilibrium can be disturbed by changes to temperature, concentration, and, in some cases, volume and pressure; volume and pressure changes will disturb equilibrium if the number of moles of gas is different on the reactant and product sides of the reaction. The system's response to these disturbances is described by Le Chatelier's principle: The system will respond in a way that counteracts the disturbance. Not all changes to the system result in a disturbance of the equilibrium. Adding a catalyst affects the rates of the reactions but does not alter the equilibrium, and changing pressure or volume will not significantly disturb systems with no gases or with equal numbers of moles of gas on the reactant and product side.
Footnotes
- 1 Herrlich, P. “The Responsibility of the Scientist: What Can History Teach Us About How Scientists Should Handle Research That Has the Potential to Create Harm?” EMBO Reports 14 (2013): 759–764.
Contributors
-
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).
-
Modified by Tom Neils (Grand Rapids Community College)

