Chromatography refers to a group of methods that are used as a way of separating mixtures of compounds into their individual components. The basic set up of a chromatographic system is to have two phases, one stationary and one mobile. A compound, which we will usually call the solute, is introduced into the system, and essentially has a choice. If it is attracted to the mobile phase (has van der Waal attractions to the mobile phase), it will move through the system with the mobile phase. If it is attracted to the stationary phase, it will lag behind. It’s easy to imagine some solute compounds with some degree of attraction for both phases, such that these move through the system with some intermediate rate of travel.
The first report of a chromatographic application was by Mikhail Tswett, a chemist from Estonia, in 1903. (A list of important literature articles is provided at the end). Undoubtedly other people had observed chromatography taking place, but no one until Tswett recognized its applicability for the separation of mixtures in chemistry. Tswett was interested in separating the pigments in plants. He packed a glass column that might have been comparable to a buret with starch, mashed up the plant and extracted the pigments into a solvent, loaded the solution onto the top of the starch column, and ran a mobile phase through the starch. Eventually he saw different color bands separate on the column, hence the term chromatography. Rather than eluting the colored bands off of the column, he stopped it, used a rod to push out the starch filling, divided up the bands of color, and extracted the individual pigments off the starch using an appropriate solvent. Twsett used a solid stationary phase (starch) and a liquid mobile phase.
Chromatographic systems can use either a gas or liquid as the mobile phase. Chromatographic systems can use either a solid or liquid as the stationary phase. A solid stationary phase is easy to imagine, as we have already seen for Tswett’s work. Another common example is to use paper as the solid (actually, paper is made from a compound called cellulose). The sample is spotted onto the paper as shown in Figure 1a, and the bottom of the piece of paper is dipped into an appropriate liquid (note that the spot is above the liquid – Figure 1b). The liquid mobile phase moves up the paper by capillary action, and components of the mixture can separate into different spots depending on their relative attraction to the cellulose or chemicals that make up the liquid (Figure 1c).

Figure 1. Paper chromatography
Another type of chromatography that you may be familiar with is thin layer chromatography (TLC). This is very similar to paper chromatography, although the stationary phase is usually a coating of small particles of a material known as silica gel (silica gel is a polymer with the formula SiO2, although a bit later we will talk in more detail about the exact chemical nature of this material) on a glass or plastic plate. Similarly, we could take these silica gel particles and pack them into a glass column, and then flow a liquid through the column. If we used some gas pressure to force the liquid through the silica gel column more quickly, we would have a common technique known as flash chromatography that synthetic chemists use to separate relatively large amounts of materials they have prepared. Another common solid to use in column chromatography is alumina (Al2O3 is the general formula, although we will say more later about its exact chemical nature).
These methods we have just been talking about are examples of liquid-solid chromatography. If we used gas as the mobile phase, injected either a gaseous sample or liquid sample into a high temperature zone that flash volatilized it, with some solid as the stationary phase (there are a range of possible materials we could use here), we could perform gas-solid chromatography. If we thought about how a solute compound would interact with such a solid stationary phase, we would realize that it must essentially “stick” to the surface by some intermolecular (van der Waal) forces. This sticking process in chromatography is known as adsorption.
Earlier I said that it is also possible to use a liquid as the stationary phase. This might seem odd at first, because it would seem as if the flowing mobile phase would somehow push along a liquid stationary phase. The way to use a liquid as the stationary phase is to coat a very thin layer of it onto a solid support, as illustrated in Figure 2.
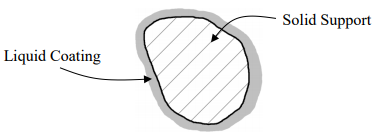
Figure 2. Liquid phase coated onto a solid support.
Alternatively, it is possible to coat a liquid phase onto the inside walls of a small-diameter, open-tubular column (known as a capillary column) as shown in Figure 3.

Figure 3. Liquid phase coated onto the inside walls of a capillary column.
The liquid coating has some attractive forces for the underlying solid surface, such that it sticks to the surface and stays in place. We could probably see how we could easily have a gas flowing around a packed bed of such particles and, so long as the liquid coating did not evaporate, it would stay in place on the particles. Flowing a liquid around it might be a bit more problematic, and we will examine that in length later in this unit. Suffice it to say, though, that it can be done. This would lead to gas-liquid and liquid-liquid chromatographic methods. The interaction of a solute compound with a liquid stationary phase is different than with the solid stationary phases discussed above. It will still depend on having attractive intermolecular forces, but instead of sticking to the solid surface by adsorption, the solute molecule will now dissolve into the liquid stationary phase. If a solute molecule dissolves into a liquid stationary phase in a chromatographic system, we say that the molecule partitions between the two phases.
These two terms are so important in chromatographic systems that it is worth summarizing them again:
Adsorption – describes the process of a solute molecule adhering to a solid surface
Partition – describes the process of a solute molecule dissolving into a liquid stationary phase
There are two terms we can describe in chromatography that are analogous to those we already described for liquid-liquid extraction. One of these is the distribution constant (KC) that is the ratio of the concentration of the solute in the stationary phase (CS) to that in the mobile phase (CM).
\[\mathrm{K_C = \dfrac{C_S}{C_M} =\dfrac{mol_S ⁄V_S}{mol_M ⁄V_M} = \dfrac{mol_S × V_M}{mol_M × V_S}}\]
But just like in liquid-liquid extraction, a problem with this ratio is that the volumes of the stationary and mobile phases might be significantly different from each other. With a solid stationary phase, VS is comparable to the surface area of the particles. With a liquid stationary phase, the coating is usually so thin that VM would be much larger than VS. In many cases, a more useful term is the partition coefficient (KX), which is the ratio of the moles of solute in each of the two phases.
\[\mathrm{K_X = \dfrac{mol_S}{mol_M}}\]
Notice that we can relate KC to KX because the mole ratio shows up in both. That allows us to write the following:
\[\mathrm{K_C = K_X \left(\dfrac{V_M}{V_S}\right)}\]
There are also some other fundamental figures of merit that we often use when discussing chromatographic separations. The first is known as the selectivity factor (\(\alpha\)). In order to separate two components of a mixture, it is essential that the two have different distribution or partition coefficients (note, it does not matter which one you use since the volume terms will cancel if KC is used). The separation factor is the ratio of these two coefficients, and is always written so that it is greater than or equal to one. K2 represents the distribution coefficient for the later eluting of the two components.
\[\mathrm{α = \dfrac{K_2}{K_1}}\]
If \(\alpha\) = 1, then there will be no separation of the two components. The larger the value of \(\alpha\), the greater the separation. One thing to realize is that there is some limit as to how large we want an \(\alpha\)-value to be. For example, the chromatogram in Figure 4b has a much greater \(\alpha\) value than that in Figure 4a. But the two components are fully separated so that the extra time we would need to wait for the chromatogram in Figure 4b is undesirable. In most chromatographic separations, the goal is to get just enough separation, so that we can keep the analysis time as short as possible.

Figure 4. Elution of compounds where the \(\alpha\)-value in (b) is much greater than the \(\alpha\)-value in (a).
Another important figure of merit in chromatographic separations is known as the retention factor (k), which is a measure of the retention of a solute, or how much attraction the solute has for the stationary phase. The k term was formerly known as the capacity factor. The retention factor is actually identical to the partition coefficient.
\[\mathrm{k = \dfrac{mol_S}{mol_M} = \dfrac{C_S V_S}{C_M V_M} = K_C \left(\dfrac{V_S}{V_M} \right)}\]
We can determine k values from a chromatogram using the following equation:
\[\mathrm{k = \dfrac{t_R - t_0}{t_0}}\]

Figure 5. Chromatographic information used to calculate the k value for a peak.
As seen in Figure 5, the term tR is the retention time of the compound of interest, whereas t0 refers to the retention time of an unretained compound (the time it takes a compound with no ability to partition into or adsorb onto the stationary phase to move through the column). Since t0 will vary from column to column, the form of this equation represents a normalization of the retention times to t0.
Another important figure of merit for a chromatographic column is known as the number of theoretical plates (N). It turns out that one helpful way to think of a chromatographic column is as a series of microscopically thin plates as shown in Figure 6. Using the picture in Figure 6, we

Figure 6. Representation of a chromatographic column as a series of microscopically thin plates.
could imagine a compound moving down the column as a series of steps, one plate at a time. The compound enters a plate, distributes according to its distribution coefficient between the stationary and mobile phase, and then moves on to the next plate. Now it turns out that chromatographic systems never really reach equilibrium, and in fact are not steady state systems, but things like the distribution and partition coefficients, which are equilibrium expressions, are useful ways to examine the distribution in chromatographic systems. A compound with less favorable solubility in the stationary phase would then move through the series of plates faster. The only way to separate two compounds is to have enough plates, or enough equilibrations, to exploit the difference in partition coefficients between the two compounds. A column with more theoretical plates is more likely to separate two compounds than one with fewer.
We can determine the number of plates for a compound as shown in Figure 7.
\[\mathrm{N = 16 \left(\dfrac{t_R}{W}\right )^2}\]
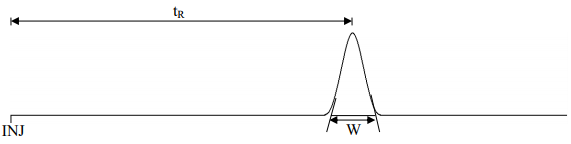
Figure 7. Chromatographic information used to determine N for a column.
W is the width of the peak where it intersects with the baseline. The important thing to remember is to use the same units when measuring W and tR (e.g., distance in cm on a plot, time in seconds, elution volume in mL – which is common in liquid chromatography). It should be pointed out that a column will have a set number of plates that will not vary much from compound to compound. The reason for this is that a compound with a longer retention time will exhibit a larger peak width, such that the ratio term is correcting for these two effects.
If we determine the number of plates for a column, dividing the column length (L) by the number of plates leads to the height equivalent to a theoretical plate (H). Note that the smaller the value of H the better. It actually turns out the H is the important figure of merit for a column.
\[\mathrm{H = \dfrac{L}{N}}\]
The chromatograms in Figure 8 show the distinction between a column with a smaller value of H (Figure 8a) and one with a much larger value of H (Figure 8b).
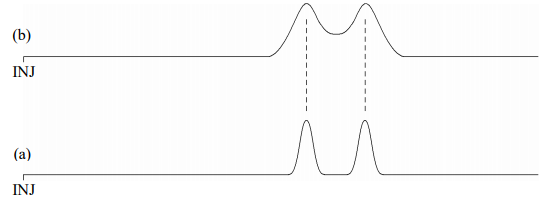
Figure 8. Chromatograms for a column with (a) a smaller value of H and (b) a larger value of H.
Usually today, though, people refer to something called the reduced plate height (h) for a column. The reduced plate height is defined as shown below, in which dp is the particle diameter of the packing material used in the column (or the internal tube diameter if an open tubular capillary column is used).
\[\mathrm{h = \dfrac{H}{d_p}}\]
You will also come across a term known as the reduced velocity (\(\nu\)) in the chromatographic literature. The reduced velocity is defined as follows, in which v is the mobile phase velocity, and DM the diffusion coefficient of the solute in the mobile phase.
\[\mathrm{\nu = \dfrac{d_p × v}{D_M}}\]
Finally, we can define an equation for the resolution (RS) of two compounds. This will be a measure of how much two compounds in a chromatogram are separated from each other.
\[\mathrm{R_S = \dfrac{2(t_2-t_1)}{W_1 + W_2}}\]
The terms t2 and t1 refer to the retention time of the two compounds, and W1 and W2 to the width of each peak at baseline.
Figure 9 shows the separation of two peaks at resolution values of 0.75 (Figure 9a), 1.0 (Figure 9b) and 1.5 (Figure 9c). The better separation of A and B that occurs with increasing resolution is obvious. It is also worth noting that the analysis time is longer the higher the resolution. Chromatographic analyses are always a compromise between the degree of separation of the peaks and how long it takes to perform the analysis. In many cases, the goal is to get just enough separation in the shortest period of time.
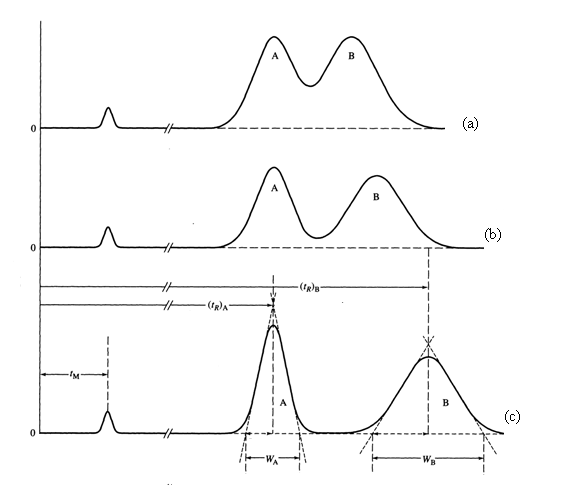
Figure 9. Separation of two peaks with resolution values of (a) 0.75, (b) 1.0 and (c) 1.5.

