Laser Theory

Energy State Populations

For reasons that we cannot explain, it appears that all things in nature prefer to go to the lowest energy state available to them. This seems to be how nature behaves. Apples fall all the way to the ground, once they are let go by the tree branches they grew on. Of course unless they fall into a hole, in which case they go even lower than the ground level - to the bottom of the hole. To raise the energy of the fallen apple someone, or something, has to intervene. A child must pick it up off the ground, for example. Otherwise, the apple will remain at its lowest point. Similarly, atoms tend to prefer to always stay in their ground state, unless some intervening force causes them to reach an excited state. In the language used in the study of lasers, any process that feeds energy into a collection of atoms or molecules and causes them to vacate their ground state is referred to as an energy pump, or simply as a pump.

In most lamps electricity is used, by one mechanism or other, to pump atoms out of their ground-state into some excited state. We have already seen that incandescent bulbs produce light from Radiative transitions after excitation via collisions of the electrons in an electric current with the filament atoms. As we've also seen, other light sources, like the fluorescent lamps or neon tubes, use gas or vapor for their medium of excitation instead of a solid filament. In most lamps, the pumping mechanism is electricity. This is also the case for most lasers, but in some lasers optical pumping is the mechanism that is used to cause excitation. In optical pumping a light source generates photons with enough energy that they are able to get absorbed by the atoms in the lasing medium and cause them to go into an excited state.

Evidently, all excitations occur "instantaneously", but de-excitations can lag by a measurable time interval that depends on the properties of the excited state. That is to say, an atom in an excited state does not instantaneously de-excite. The time that it spends, on average, in that excited level is called the lifetime of that state. Lifetimes can vary in duration depending on the atom and on the energy level. Excited state lifetimes are typically a few nanoseconds (10-9 s, or a billionth of a second), but they could be as short as a picosecond (10-12 s, or a thousand times shorter still) or as long as a few milliseconds (10-3 s). The ground state, of course, has an infinitely long lifetime since an atom in its ground state can no longer decrease its energy. So, the most stable of states is the ground state. Long-lived states are referred to as meta-stable states.

In the case of Radiative emission, atoms happen to take two very distinctly different approaches: spontaneous emission, or stimulated emission. Spontaneous emission refers to the case when the excited atom de-excites, rather randomly whenever it "feels like it", and emits a photon. This photon has an energy equal to the difference between the two energy levels of the transition, but its direction of travel and its other properties, such as polarization are random. Stimulated emission was first theorized by Albert Einstein in 1917. For stimulated emission to occur a second, non-participating yet stimulating, photon must be present. The energy of this second photon must exactly match the allowed energy of the transition. Then the emitted photon will not only have the same energy as the stimulating one, but it will also travel in the same direction, and will be essentially identical to it.

So, independent of what type of medium is used in a laser, in the absence of a pump the atoms or molecules are almost all in their ground state. Let us imagine that we could count the number of atoms in our laser medium that are in each energy state and denote the ones which are in their ground state by Ngs , those in the first excite state by N1, those in the second excited state by N2 , and so on. Then in the absence of a pump we are mostly certain that N1= N2 = ... = 0, and Ngs = total number of all the atoms in the medium. Once the pump is turned on it will deplete the number of atoms that were originally in the ground state and increases the number of atoms in the excited states that it is pumping to. Because excited atoms de-excite quickly and return to their ground states by spontaneous emission, in almost all lasers even when the pump is feeding energy into the medium the number of atoms in their ground state remains many times more than atoms in any other energy state. That is to say, almost always we could safely state that:

N_{ground state} much bigger than N_{any other state} .

To make a laser we need to not only excite the atoms in the laser medium, but somehow encourage them to undergo a decay through stimulated emission. In stimulated emission a passer-by photon which has an energy exactly equal to the transition energy stimulates the atom to emit a photon, identical to the passer-by photon, instantly. The problem with this is that the same passer-by photon could instead get absorbed by a de-excited atom. So, aside from pumping the atoms to excited states, we need to use clever procedures to insure that there are more excited atoms that could use the passer-by photon for stimulated emission than there are de-excited atoms which could absorb it; i.e. we need to generate a population inversion. Although Einstein predicted stimulation emission in 1917, it was not found experimentally for over 10 years and took over another 30 years just to predict the possibility of a laser. This is basically because it was not considered possible to produce a population inversion because of the above inequality.

Lasing in Two-Level Systems

For the sake of our studies, let's first consider a laser medium whose atoms have only two energy states: a ground state and one excited state. In such an idealized atom the only possible transitions are excitation from the ground state to the excited state, and de-excitation from the excited state back into ground state. Could such an atom be used to make a laser?

There are several important conditions that our laser must satisfy. First of all, the light that it produces must be coherent. That is to say, it must emit photons that are in-phase with one another. Secondly, it should emit monochromaticlight, i.e. photons of the same frequency (or wavelength).Thirdly, it would be desirable if our laser's output were collimated, producing a sharply defined "pencil-like" beam of light (this is not crucial, but clearly a desirable condition). Lastly, it would also be desirable for our laser to be efficient, i.e. the higher the ratio of output energy - to - input energy, the better.

Let us begin by examining the requirements for our first condition for lasing, coherence. This condition is satisfied only when the lasing transition occurs through stimulated emission. As we have already seen, stimulated emission produces identical photons that are of equal energy and phase and travel in the same direction. But for stimulated emission to take place a "passer-by" photon whose energy is just equal to the de-excitation energy must approach the excited atom before it de-excites via spontaneous emission. Typically, a photon emitted by the spontaneous emission serves as the seed to trigger a collection of stimulated emissions. Still, if the lifetime of the excited state is too short, then there will not be enough excited atoms around to undergo stimulated emission. So, the first criteria that we need to satisfy is that the upper lasing state must have a relatively long lifetime, otherwise known as a meta-stablestate, with typical lifetimes in the milliseconds range. In addition to the requirement of a long lifetime, we need to ensure that the likelihood of absorption of the "passer-by" photons is minimized. This likelihood is directly related to the ratio of the atoms in their ground state versus those in the excited state. The smaller this ratio, the more likely that the "passer-by" photon will cause a stimulated emission rather than get absorbed. So, to satisfy this requirement, we need to produce a population inversion: create more atoms in the excited state than those in the ground state.

Achieving population inversion in a two-level atom is not very practical. Such a task would require a very strong pumping transition that would send any decaying atom back into its excited state. This would be similar to reversing the flow of water in a water fall. It can be done, but is very energy costly and inefficient. In a sense, the pumping transition would have to work against the lasing transition.

Figure 1: Stimulated emission in a two-level transition. Image used with permission (CC BY-SA 4.0; V1adis1av)

It is clear, from the above diagram, that in the two-level atom the pump is, in a way, the laser itself! Such a two-level laser would work only in jolts. That is to say, once the population inversion is achieved the laser would lase. But immediately it would end up with more atoms in the lower level. Such two-level lasers involve a more complicated process. We will see, in later material, examples of these in the context of excimer lasers, which are pulsed lasers. For a continuous laser action we need to consider other possibilities, such as a three-level atom.

Lasing in Three-Level Systems

In fact, the first laser that was demonstrated to operate was a three-level laser, Maiman's ruby laser.

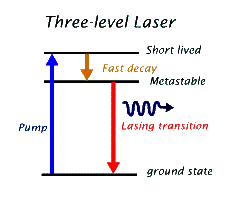
In the above diagram of a three level laser the pump causes an excitation from the ground state to the second excited state. This state is a rather short-lived state, so that the atom quickly decays into the first excited level. [Decays back to the ground state also occur, but these atoms can be pumped back to the second excited state again.] The first excited state is a long-lived (i.e. metastable) state which allows the atom to "wait" for the "passer-by" photon while building up a large population of atoms in this state. The lasing transition, in this laser, is due to the decay of the atom from this first excited metastable state to the ground state. If the number of atoms in the ground state exceeds the number of atoms that are pumped into the excited state, then there is a high likelihood that the "lasing photon" will be absorbed and we will not get sustained laser light. The fact that the lower lasing transition is the ground state makes it rather difficult to achieve efficient population inversion. In a ruby laser this task is accomplished by providing the ruby crystal with a very strong pulsating light source, called a flash lamp. The flash lamp produces a very strong pulse of light that is designed to excite the atoms from their ground state into any short-lived upper level.t In this way the ground state is depopulated and population inversion is achieved until a pulse of laser light is emitted. In the ruby laser the flash lamp light lasts for about 1/1000 of a second (1 ms) and can be repeated about every second. The duration of the laser pulse is shorter than this, typically 0.1 ms. In some pulsed lasers the pulse duration can be tailored using special methods to be much shorter than this, down to about 10 fs (where 1 fs = 10-15 s or one thousandth of a millionth of a millionth of a second). So, the output of a three-level laser is not continuous, but consists of pulses of laser light.

Lasing in Four-Level Systems

To achieve a continuous beam of laser light a four-level laser is required.

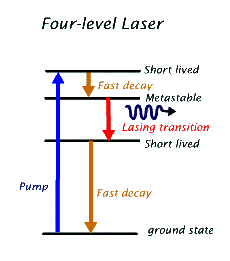
Here, the lower laser level is not the ground state. As a result, even a pump that may not be very efficient could produce population inversion, so long as the upper level of the laser transition is longer lived than the lower level. Of course, all attempts are made to design a pump that maximizes the number of excited atoms. A typical four-level laser is the helium-neon (He-Ne) gas laser. In these lasers electric pumping excites helium atoms to an excited state whose energy is roughly the same as the upper short-lived state in the neon atom. The sole purpose of the helium atoms is to exchange energy with neon atoms via collisional excitation. As it turns out, this is a very efficient way of getting neon atoms to lase.

Laser components

All lasers have three primary components:

• Medium
• Pump
• Resonant Cavity

The laser medium can be gaseous, liquid, or a solid. These could include atoms, molecules, or collections of atoms that would be involved in a laser transition. Typically, a laser is distinguished by its medium, even though two lasers using different media may have more in common than two which have similar media.

There are three different laser pumps: electromagnetic, optical, and chemical. Most lasers are pumped electro-magnetically, meaning via collisions with either electrons or ions. Dye lasers and many solid state lasers are pumped optically; however, solid state lasers are typically pumped with a broad band (range of wavelengths) flash-lamp type light source, or with a narrow band semiconductor laser. Chemically pumped lasers, using chemical reactions as an energy source, are not very efficient. So far, these lasers have been made to work not so much for their usefulness as for their curious operation.

Up to now in our discussion of laser theory we have not really seen how the beam is generated. We know that photons emitted by stimulated emission travel coherently in the same direction, but what is it that defines the beam direction and what allows the intensity of the laser light to get large? The answer to these two questions is coupled together in the resonant cavity. Laser resonant cavities usually have two flat or concave mirrors, one on either end, that reflect lasing photons back and forth so that stimulated emission continues to build up more and more laser light. The "back" mirror is made as close to 100% reflective as possible, while the "front" mirror typically is made only 95 - 99% reflective so that the rest of the light is transmitted by this mirror and leaks out to make up the actual laser beam outside the laser device.

The resonant cavity thus accounts for the directionality of the beam since only those photons that bounce back and forth between the mirrors lead to amplification of the stimulated emission. Once the beam escapes through the front mirror it continues as a well-directed laser beam. However, as the beam exits the laser it undergoes diffraction and does have some degree of spreading. Typically this beam divergence is as small as 0.05o but even this small amount will be apparent if the beam travels long distances.

Even more, the resonant cavity also accounts for the amplification of the light since the path through the laser medium is elongated by repeated passes back and forth. Typically this amplification grows exponentially, similar to the way compound interest works in a bank. The more money in your bank account, with compound interest, the faster you earn more interest dollars. Similarly, the more photons there are to produce stimulated emission, the larger the rate at which new coherent photons are produced. The term used for laser light is gain, or the number of additional photons produced per unit path length.

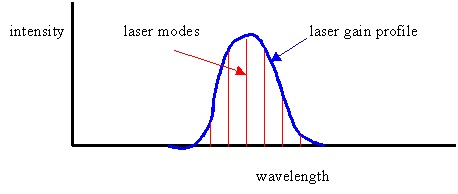
The last question to address in this section is: why is the resonant cavity called by that name? What does resonance have to do with having mirrors on either end of a region containing the laser medium? Recall that when we discussed resonance on a string, we spoke about the wave traveling one way along the string (say to the right) interfering with the wave reflected at the end traveling back to the left. At a resonant frequency, there are points at which the two waves exactly add or cancel all the time, leading to a standing wave. At other frequencies the waves will randomly add or cancel and the wave will not have a large amplitude. The case of a light wave traveling back and forth in the resonant cavity is exactly analogous in that only at certain resonant frequencies will the light wave be amplified. The required condition is easy to see. The mirror separation distance, L, must be equal to a multiple of half a wavelength of light, just as we saw in the case of a string. In symbols, we have that L = nl/2, where l is the wavelength of the light and n is some integer. In the case of light, because of the small wavelength n is a very large number, implying that there are a huge number of resonant frequencies. On the other hand, only those resonant frequencies that are amplified by the laser medium will have large amplitudes and so usually there are only a few so-called laser modes or laser resonant frequencies present in the light from a laser, as shown in the figure.

Questions on Laser Components

• What are the three primary components of a laser?
• What different types of laser medium are used?
• What is a pump? Describe the different types of pumps.
• What is a resonant cavity?
• Describe how the resonant cavity produces a collimated laser beam.
• What is the beam divergence of a laser caused by? What is a typical value for it?
• What does the term gain mean? Is it related to pain?
• Describe why a typical laser has only a few modes, while the resonant cavity produces a huge number of them.

Contributors

• Jay Newman and Seyffie Maleki (Union College)