5.9: Energy in Chemical Reactions
- Page ID
- 285305
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In addition to changes in the distribution of mass among various chemical species that occur with chemical reactions, another important participant in chemical reactions is energy. Chapter 15 defines and discusses energy in more detail. Here energy is considered in the form of heat manifested by the movement of atoms and molecules and as chemical energy, which is energy stored in chemical bonds in matter. The standard unit of energy is the joule, abbreviated J. A total of 4.184 J of heat energy will raise the temperature of 1 g of liquid water by 1 ̊C.
As an example of energy involved with chemical reactions, Consider what happens in a burner on a kitchen range fueled by natural gas. The flame is obviously hot; something is going on that is releasing heat energy. The flame is also giving off light energy, probably as a light blue glow. A chemical reaction is taking place as the methane in the natural gas combines with oxygen in the air,
\[\ce{CH4 + 2O2 \rightarrow CO2 + 2H2O}\]
to produce carbon dioxide and water. Most of the energy released during this chemical reaction is released as heat, and a little bit as light. It is reasonable to assume that the methane and oxygen contain stored energy as chemical potential energy and that it is released in producing carbon dioxide and water. Common sense tells us that it would be hard to get heat energy out of either of the products. They certainly won’t burn! Water is used to put out fires, and carbon dioxide is even used in fire extinguishers.
The potential energy contained in chemical species is contained in the chemical bonds of the molecules that are involved in the chemical reaction. Figure 5.2 shows the kinds of bonds involved in methane, elemental oxygen, carbon dioxide, and water and the energy contained in each. The bond energies are in units of the number of kilojoules (thousands of joules, kJ) required to break a mole (6.02×1023, see Section 4.8) of the bonds (kJ/mol). The same amount of energy is released when a mole of a bond is formed. By convention, energy put into a system is given a positive sign and energy released is denoted by a negative sign.
To calculate the energy change when a mole of methane reacts with oxygen as shown in Reaction 5.9.1, the difference is taken between the sum of the energies of the bonds in the products and the sum of the energies of the bonds in the reactants. Examination of Reaction 5.9.1 and Figure 5.2 shows the following total bond energies in the products:
\(\textrm{1 mol CO}_{2} \times \frac{\textrm{2 mol C=O}}{\textrm{mol CO}_{2}} \times \frac{\textrm{799 kJ}}{\textrm{mol C=O}} = \textrm{1598 kJ}\)
\(\textrm{2 mol H}_{2}\textrm{O} \times \frac{\textrm{2 mol O-H}}{\textrm{mol H}_{2}\textrm{O}} \times \frac{\textrm{459 kJ}}{\textrm{mol O-H}} = \textrm{1836 kJ}\)
A similar calculation gives the total bond energies in the reactants
\(\textrm{1 mol CH}_{4} \times \frac{\textrm{4 mol C-H}}{\textrm{1 mol CH}_{4}} \times \frac{\textrm{411 kJ}}{\textrm{mol C-H}} = \textrm{1644 kJ}\)
\(\textrm{2 mol O}_{2} \times \frac{\textrm{1 mol O=O}}{\textrm{mol O}_{2}} \times \frac{\textrm{494 kJ}}{\textrm{mol O=O}} = \textrm{988 kJ}\)
Total bond energy in reactants = 1644 kJ + 988 kJ = 2632 kJ
The difference in bond energies between products and reactants is 3434 kJ - 2632 kJ = 802 kJ
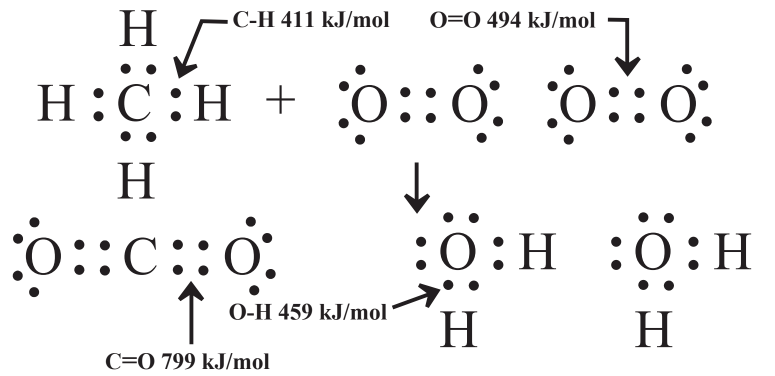
This calculation states that, based upon considerations of bond energy, alone, the energy released when 1 mole of CH4 reacts with 2 moles of O2 to produce 1 mole of CO2 and 2 moles of H2O, is 802 kJ. This is an exothermic reaction in which heat energy is released, so it is denoted as-802 kJ. This value is close to the value that would be obtained by experimentally measuring the heat energy released by the reaction, assuming all the reactants and products were in the gas phase. (A significant amount of heat energy is released when vapor-phase water condenses to liquid. Highly efficient condensing gas furnaces capture this heat in a heat exchanger where the water vapor in the furnace exhaust condenses to the liquid phase.) For the most part, therefore, the amount of heat energy released in a chemical reaction, and the amount of potential chemical energy contained in the reactants is equal to the difference between the total bond energies of the products and those of the reactants.


