Colorimetric Fe Analysis (Experiment)

In the colorimetric analysis for Mn the concentration of the Mn is determined using the characteristic color of the permanganate ion. However, few metal ions show such strong colors, particularly at low concentrations. Fortunately many highly colored complexes can be formed from metal ions and organic or inorganic complexing agents. These complexes are the result of the interaction of a Lewis acid (the metal ion) and a Lewis base (the complexing agent). The ideal color-forming reagent should be stable and selective (even specific) and react rapidly to form soluble, highly colored complexes. The colored complex should have a high absorptivity and be free from variations in color due to minor changes in pH or temperature.

The application of colorimetric reagents is not a new technique but dates back nearly two thousand years. Around 60 A.D. Pliny the Elder in his "Natural History" recommended the use of nutgall as a reagent for the determination of iron in verdigris, which is a green pigment. Nutgall contains about 65-70% tannic acid which when combined with iron leads to the formation of a black irontannate complex.

In general organic colorimetric reagents are considerably more sensitive than are inorganic ones. They give more intense colors and are therefore frequently used for trace analyses. With many organic reagents, it is possible to determine concentrations at the ppm level. 2,2'-Bipyridyl (bipy), gfw = 156.20, forms an intensely red complex with iron(II) which may be exploited to determine iron concentrations in the ppm range. The reaction is:

\[3bipy + Fe^{2+} \rightleftharpoons Fe(bipy)_3^{2+}\]

The figure below shows the structure of the reagent and the complex formed with Fe.

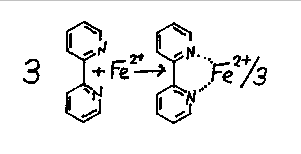
The complex conforms to an octahedral geometry with coordinate covalent bonds being formed between the adjacent sp³d² hybrid orbitals of the Fe²⁺. The complex is chiral; there are left-handed and right-handed non-superimposable optically active forms. Can you draw the two? The molar absorptivity of the iron-bipyridyl complex is 8650 L/mol/cm at the wavelength of maximum absorbance. The complex forms rapidly, is stable over the pH range 3 to 9, and may be used to determine iron(II) concentrations in the range of 0.5 to 8 ppm.

Iron(III), if present, must be reduced to iron(II) to produce the colored species. A suitable reagent for this purpose is hydroxylamine hydrochloride, \(\ce{HONH3^{+}Cl^{-}}\). The reaction for this reduction is shown below:

\[\ce{2HONH_3^+Cl^- + 2Fe^{3+} \rightleftharpoons 4H^+ + 2 H_2O + N_2 + 2Fe^{2+} + 2Cl^{-}}\]

The concentration of iron in the sample could be calculated from Beer's Law however in this procedure we employ a different method. We will prepare a standard solution and compare absorbance readings of the sample and the standard solution. This technique minimizes the effects of instrument and solution variation. Spectrophotometric methods are normally accurate to about ± 1%, i.e. to about three significant figures. Even though higher accuracy and precision can be obtained with more sophisticated instruments, in most cases an accuracy of ± 1%, at concentration levels of parts per million, is quite sufficient. The ferrous ammonium sulfate standard that is used in the procedure is normally not considered a primary standard, however it is available in a purity greater than 99% and is therefore adequate for our purposes.

A major source of error in this experiment is misuse of the Spectronic 20 spectrophotometer. Before you take any measurements on this instrument read the instructions at the end of this manual and commit them to memory. There is also a useful Web page available via the instructor's home page which gives you the same information.

Experimental

Preparation of the Original Fe Solution

To an accuracy of ± 0.1 mg weigh out enough ferrous ammonium sulfate, Fe(NH₄)₂(SO₄)₂6H₂O, gfw = 392.14, to prepare 250 mL of a solution which is 0.00200 M with respect to that compound. Quantitatively transfer the salt into a 250 mL volumetric flask, add sufficient water to dissolve the salt, add 8 mL of 3 M H₂SO₄, dilute to the mark with distilled water and mix well. We shall call this the Stock Fe Solution. Pipet 10 mL of this solution into a 100 mL volumetric flask, add 4 mL of 3 M H₂SO₄ and dilute to the mark with distilled water and mix well. Label this solution as Original Fe Solution and calculate the concentration of Fe, in ppm, in this solution.

Measurement of the Absorbance Spectrum

In order to determine the wavelength of maximum absorbance it is necessary to obtain the absorbance spectrum of the iron-bipyridyl complex. Readings taken at 10 nm intervals are sufficient to outline an absorbance spectrum except perhaps at absorbance peaks where additional points may be required to characterize the curve more completely. Pipet 10 mL of the Original Fe Solution into a 50 mL volumetric flask. Into a second 50 mL volumetric flask do not add any of the iron solution, but add about 10 drops of 3 M H₂SO₄. Then, in the order stated, add to each flask 1 mL of 10% hydroxylamine hydrochloride solution, 10 mL of 0.1% bipyridyl solution and 4 mL of 10% sodium acetate solution. The purpose of the sodium acetate is to buffer the mixture. The sodium acetate plus the sulfuric acid already present gives an acetic acid-acetate buffer in the pH region of about 4.5 to 5. Be sure to mix well after the addition of each reagent. Then fill each flask to the mark with distilled water and mix well by inverting and shaking. The flask containing iron has the same concentration as the Standard Fe Solution which will be prepared in the next section. Now take absorbance readings for this solution from 400 nm to 600 nm, in intervals of 10 nm, except where additional points are needed better to define the shape of the curve. Use the solution not containing Fe as a blank. Neatly plot the absorbance (vertical axis) against wavelength (horizontal axis) on a piece of millimeter graph paper. Use the long side of the paper as the horizontal axis. From this graph select the wavelength which exhibits the maximum absorbance. That is the wavelength to be used for the measurement of the unknown solution. It is called lambda (max).

Determination of the Absorbance of the Standard Fe Solution.

Before beginning this part of the procedure be sure to record the number of the colorimeter that you are using for this part of the analysis. The number of the colorimeter is found on a small blue tag on the front of the colorimeter. A11 further absorbance measurements must be made with the same colorimeter and the same cuvettes in order for this method to work. Discard both of the solutions in the 50 mL volumetric flasks. Thoroughly rinse both volumetric flasks and then prepare a new set of solutions from the Original Fe Solution using the same amounts according to the previous procedure. Label the solution containing the Fe as Standard Fe Solution and calculate its Fe concentration in ppm. Determine the absorbance of this solution at the wavelength of maximum absorbance previously determined. For a blank use the solution which does not contain Fe. Make at least three measurements. In each case reset the zero and the 100% transmission. Record both the percent transmission and absorbance values. Empty your cuvette and refill it with another portion of the same solution and again determine the absorbance value. Calculate the average of all six absorbance values.

Analysis of the Fe Unknown

Clean a 100 mL volumetric flask, place your initials on the ground glass area and hand it to your instructor who will pipet 10 mL of unknown solution into it and who will also give you an unknown number for it. Then add 4 mL of 3 M H₂SO₄, mix well and then make up to the calibration mark with distilled water. Mix well by inverting and shaking the stoppered flask. Label this solution as First Unknown Dilution (FUD). Pipet 10 mL of this solution into a 50 mL volumetric flask and then in this exact order add 1 mL of 10% hydroxylamine hydrochloride solution, 10 mL of 0.1% bipyridyl solution and 4 mL of 10% sodium acetate solution. Be sure to mix well after the addition of each reagent, by gently shaking or swirling, but not inverting, the flask. After all reagents have been added fill the flask to the mark with distilled water and mix well by inverting and shaking. This solution will be called the Second Unknown Dilution (SUD). Determine the absorbance of the this solution using the previous blank solution as the reference and the wavelength of maximum absorbance determined earlier. Measure the absorbance at least three times. Empty the cuvette and refill it with another portion of solution and again determine the absorbance.

Analysis of city tap water

If samples of city tap water are supplied in this experiment, you will determine the iron concentration in two samples. The concentration of iron in city tap water approaches the level of precision of this method because the concentration of iron in most water of southern California is very low. Iron pipes offer the most abundant source for the iron in our water. The K_sp of Fe(OH)₃ is 4.0 x 10^-38. Calculation yields a concentration of Fe³⁺ in neutral water to be so low as to be undetectable -- on the order of one part iron per one quintillion parts of water (10^-18). Still, whatever iron that finds its way into our water supply may end up in the form of a colloidal precipitate of ferric hydroxide. To bring that small amount of iron into solution we acidify tap water and boil it for two minutes, cool it to room temperature in ice and carry out the procedure now familiar to you.

Procedure

The absorbance you observe may be lower than that which you observed for your known and unknown samples. If you have really low absorbance readings, a slight difference in the shape of two cuvettes is enough to make detection of the presence of any iron impossible unless a correction for the systematic error between the two cuvettes is taken into account. Clean two cuvettes and fill both with the blank solution. Calibrate the spectrophotometer using one, then take an absorbance reading with the other. Make sure that the vertical line on the cuvettes is adjacent to the mark on the plastic cuvette holder in the spectrophotometer for both the calibration and all future readings. If the vertical line is in a different position during any reading, the absorance will change slightly. The second cuvette will be the one in which you place your sample. We will call this absorbance A_{systematic error} . The absorbance you measure is the systematic error between the two cuvettes, using the first cuvette as the blank. This absorbance will be subtracted from the readings you get using the iron samples, as follows: Using a 50 mL graduated cylinder, obtain two samples of city tap water, 50 mL each, from two different cities. Place each sample in a clean 250 mL beaker. Add 10 drops of 3 M H2SO4 to each. Boil each sample on a hot plate for 2 minutes. Cool the two samples in ice until they are no longer warm to the touch. Pour each in turn back into the 50 mL graduated cylinder and add enough distilled water to bring each back to 50 mL volume. Pour contents of each into the same 250 mL beakers to mix. Pipet 35 mL of the first sample into a 50 mL volumetric flask (use a 25 mL volumetric pipet and a 10 mL volumetric pipet), then in this exact order add 1 mL of 10% hydroxylamine hydrochloride solution, 10 mL of 0.1% bipyridyl solution and then finally, using an eye dropper, add up to 4 mL of 10% sodium acetate solution to the mark. Be sure to mix well after the addition of each reagent, by gently inverting the flask. This sample will be called the city reaction flask in the description of calculations below. Determine the absorbance of this solution using the previous blank solution as the reference at the wavelength of maximum absorbance determined earlier. Measure the absorbance at least three times. Repeat this section with the second boiled sample of tap water from a different city. Subtract the absorbance which represents the systematic error between the cuvettes from each of these experimental values.

Calculations

The calculation of the Fe concentration of the unknown can be made by a comparison method. This, however, can only be done if the system adheres to Beer's Law in the range of concentrations involved. In the case of the iron-bipyridyl complex that range is 0.5 to 8 ppm. The appropriate relationship for the calculation of the Fe concentration in the Second Unknown Dilution is:

\[[Fe]_{SUD} = \dfrac{A_{SUD} [Fe]_s}{A_s}\]

"A" is the absorbance, the subscript "S" refers to the absorbance and concentration, respectively, of the Standard Fe Solution while the subscript "SUD" refers to the absorbance and concentration of the Second Unknown Dilution. For the absorbance value of the unknown solution use the average of the three readings obtained for each sample taken. From the value obtained for [Fe]_SUD, calculate the concentration of iron, in parts per million, of the original unknown Fe solution given to you by your instructor.

If city water was provided for this experiment, the equation above is used to determine [Fe] for the solution whose absorbance you measured. Since this solution was made to 50 mL but in the process you used 15 mL of reagents prepared with distilled water, [Fe] for the city water can be found through a simple modification of the equation above:

Report

Report the following data:

1. Fe unknown number
2. Colorimeter number
3. Wavelength of maximum absorbance
4. Average absorbance of the Standard Fe Solution
5. Concentration of the Standard Fe Solution in ppm
6. Absorbances of the two samples of Second Unknown Dilution (SUD)
7. The average concentration of the Second Unknown Dilution in ppm.
8. Use the value given in 7, above, to calculate the original concentration in ppm Fe in the solution given you by your instructor. (To get to that point, you performed two dilutions: (a) 10:100 and (b) 10:50)
9. ppm iron in the two samples of city water, if provided for this experiment.
10. Pages in your lab notebook containing the pertinent data

Attach the original or a copy of the absorbance spectrum to the report sheet.

Questions on Colorimetric Iron

1. What is the name and structural formula of the ligand used in this procedure?
2. Draw the structural formula for the complex formed between Fe²⁺ and the ligand.
3. Why is hydroxylamine hydrochloride used in this procedure?
4. What is the formula of ferrous ammonium sulfate hexahydrate?
5. Why is sodium acetate used in this analysis?
6. Over what range of iron concentrations does the iron-bipyridyl complex obey the Beer-Lambert law?
7. Tea contains a significant amount of tannic acid. Given this fact explain why a cup of tea made with distilled water does not show the characteristic dark brown color of tea made with ordinary water.
8. List some characteristics of a good complexing agent for colorimetric analyses.
9. Calculate the ppm Fe in your Stock Fe Solution.

Contributors and Attributions

• Ulrich de la Camp and Oliver Seely (California State University, Dominguez Hills).